Вычисление значения t и z критериев

Многие критерии для проверки гипотез (интересующие нас критерии не являются исключением) вычисляются по следующему принципу:

Для проверки гипотезы о равенстве средних для двух независимых выборок «наблюдаемым значением» будет являться разница между средними двух групп, то есть . «Ожидаемое значение» или, в нашем случае, «истинное значение», то, которое существует в реальности в генеральной совокупности, обозначим как , или «истинное» среднее первой группы минус «истинное» среднее второй группы.

Теперь нам осталось посчитать стандартную ошибку. Естественно, она будет отличаться для z-критерия и для t-критерия. Начнем с z-критерия.

z-критерий

Представим, что мы сделали не две выборки, для которых посчитали разницу между двумя средними ( ), а произвели бесконечное число сравнений пар таких выборок. Тогда получим некоторое число разностей между средними и можем посчитать стандартное отклонение для распределения таких разностей. Посчитанное нами стандартное отклонение и будет являться интересующей нас стандартной ошибкой или пределом, в рамках которого будет варьироваться разность между средними, существующая в реальности в генеральной совокупности.

Формула стандартной ошибки разности между двумя средними будет выглядеть следующим образом: , где и – величины стандартного отклонения генеральной совокупности⁶ для первой и второй групп; n₁ и п₂ – число наблюдений в первой и второй группах (объем выборок).

Зная стандартную ошибку, можем записать общую формулу для z-критерия:

,

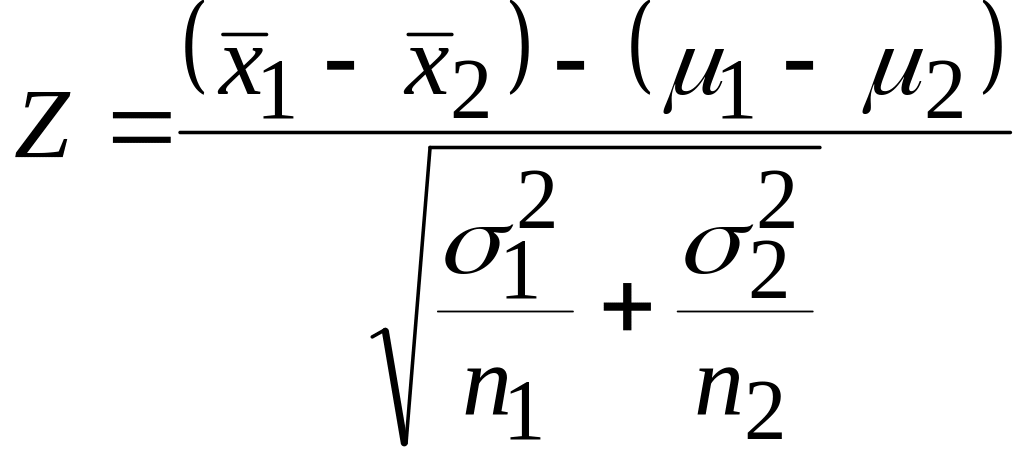где и – средние первой и второй выборок; и – средние, существующие в реальности в генеральной совокупности. (При нулевой гипотезе – поэтому нередко можно встретить формулу для z-критерия, где числитель состоит только из ( ); и – величины стандартного отклонения генеральной совокупности, для первой и второй групп; n₁ и п₂ – число наблюдений в первой и второй группах (объем выборок).

t-критерий

Логика построения этой формулы, естественно, такая же, как и для предыдущей, только здесь при вычислении стандартной ошибки будет присутствовать число степеней свободы.

t-критерий для выборок с равными дисперсиями: 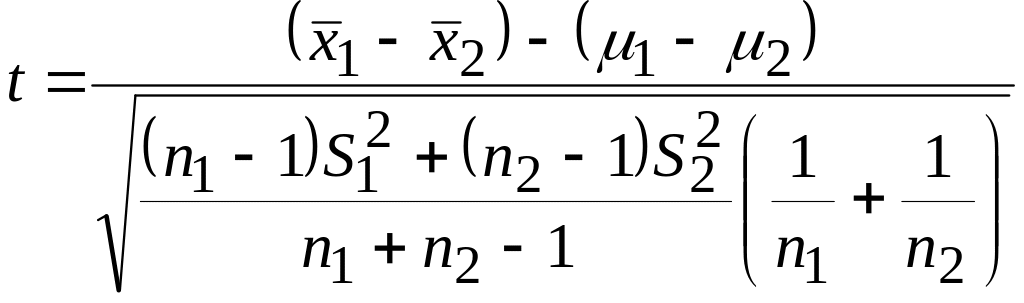; обозначения те же что и для z-критерия (см. выше).

t-критерий для выборок с неравными дисперсиями: .

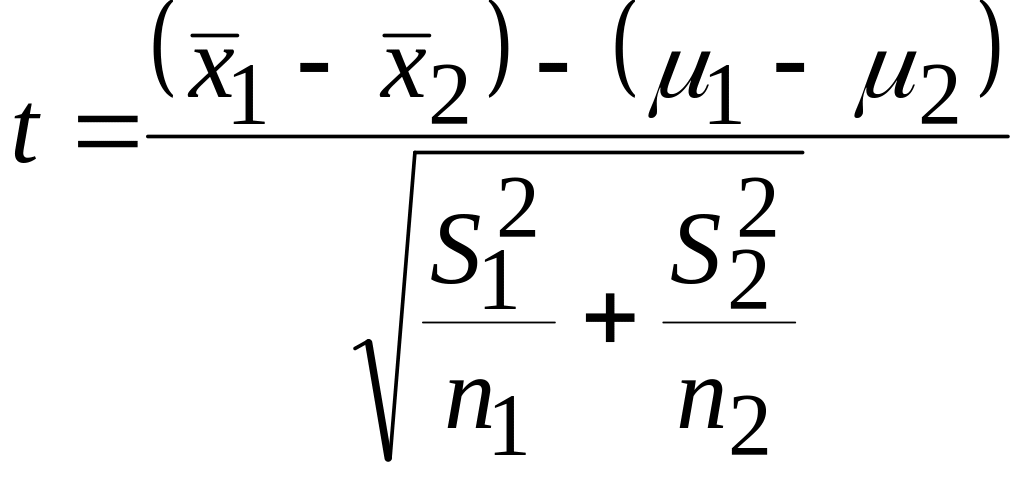На этом мы завершаем теоретическое рассмотрение логики проверки статистических гипотез о равенстве средних. Настоящий исследователь-социолог кроме теоретической грамотности должен иметь и практические навыки владения компьютером. Очевидно, что большой объем информации невозможно обработать вручную без применения компьютерных программ.

Вычисление в spss

Для начала вспомним два вопроса с установкой и без установки (см. пример №3):

Вопрос №1 без установки	Вопрос №2 с установкой
1. Сколько вы готовы заплатить за натуральный йогурт? 3 – 4руб. 4 – 5руб. 5 – 6руб. 6 – 7руб. 7 – 8руб. 8 – 9руб.	1. Сколько вы готовы заплатить за натуральный йогурт, если известно, что люди, потребляющие йогуртовые культуры, страдают на 10-15% меньше от заболеваний желудка? 3 – 4руб. 4 – 5руб. 5 – 6руб. 6 – 7руб. 7 – 8руб. 8 – 9руб.

Предполагается, что респонденты, отвечающие на вопрос с положительной установкой, будут готовы заплатить за йогурт в среднем больше, чем респонденты, отвечающие на вопрос без установки. Итак, мы опросили две группы респондентов: одной группе мы задавали вопрос с установкой, другой – без установки. Рассчитаем для них средние и z-критерий для того, чтобы узнать, влияет ли установка вопроса на ответ респондента, действительно ли совпадают (или не совпадают) средние наших двух групп (подробнее о выдвигаемой нами гипотезе см. таблица №1, пример №3). Выберите в меню:

Statistics => Compare means => Independent Samples Т Test.

В окошко Test Variable(s) переносим переменную «цена», а в окошко Grouping Variable – переменную «группа»⁷. Нажимаем Define Groups и в Group 1 ставим цифру 1, а в Group 2 - цифру 2. Далее: Continue, OK. Первая таблица, которая у нас получилась:

Group Statistics

Мы видим, что полученные нами средние близки друг к другу, что стандартные отклонения для обоих распределений практически равны. Смотрим таблицу дальше:

Independent Samples Test

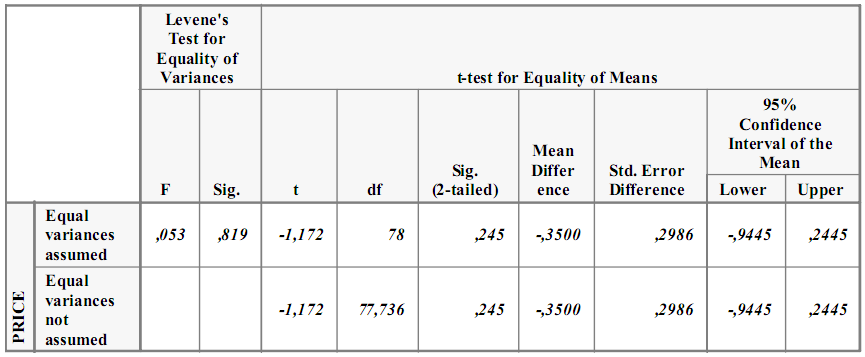
Вторая таблица разбита на две части: первая строка для групп с равными дисперсиями, вторая для групп с неравными дисперсиями. Первые два столбика – Критерий Ливиня для проверки гипотезы о равенстве дисперсий. Он применяется для того, чтобы определить, различается ли разброс в разных группах. Нулевая гипотеза говорит, что дисперсии двух совокупностей равны. Если полученный уровень значимости⁸ (Sig.) мал (например, меньше 0,05), то для средних следует использовать t-критерий для неравных дисперсий (нижняя строчка). В нашем случае F-статистика равна 0,053 со значимостью 0,819, что говорит в пользу t-критерия для равных дисперсий (верхняя строчка).

Итак, мы пользуемся верхней строчкой: t-критерий для равных дисперсий равен –1,172 и его значению соответствует полученная значимость 0,245. Это говорит о том, что наша нулевая гипотеза подтверждается: выборочные средние получены из совокупностей с одинаковыми генеральными средними, то есть в данном случае наличие установки в вопросе не повлияло на выбор респондентом ответа.

Если бы полученный уровень значимости был менее 0,05, мы бы отвергли нулевую гипотезу и признали бы наличие разности между средними.

ЛИТЕРАТУРА

1. Sam Kash Kachigan Statistical Analysis, Radius Press, New York.

2. SPSS Base 7.5 для Windows Руководство по применению.

3. Девятко И.Ф. Методы социологического исследования. – Екатеринбург, Издательство Уральского университета, 1998.

4. Елисеева И.И., Юзбашев М.М. Общая теория статистики. – Москва, Финансы и статистика, 1999.

5. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. – Москва, ИНФРА-М, 2000.

6. Калинина В.Н., Панкин В.Ф., Математическая статистика. – Москва, Высшая школа, 1998.

7. Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере. – Москва, ИНФРА-М, 1998.

1 В иностранной литературе наряду с термином «зависимые выборки» используют термин «парные выборки» (pared samples).

2 Далее в наших примерах и рассуждениях мы будем пользоваться простой случайной повторной выборкой.

3 Понятно, что нулевая и содержательная гипотеза не обязательно должны противоречить друг другу. Может быть и так, что, принимая нулевую гипотезу, мы примем и содержательную.

4 В данной работе речь будет идти только о критериях для независимых выборок, но, тем не менее, мы поговорим о том, как отличить зависимую выборку от независимой.

5 Что значит «достаточно большая» выборка, сказать однозначно нельзя. Некоторые считают, что это выборка объемом более 30 респондентов, некоторые – более 100 респондентов. Это должно определяться опытом исследователя и реальной социологической задачей.

6 Если нам не известно значение генеральной дисперсии, мы можем при достаточно больших выборках заменить его значениями выборочных дисперсий.

7 Мы приписываем респонденту принадлежность к той или иной группе, в зависимости от того, на какой вопрос он отвечал.

8 Следует отличать уровень значимости, который мы выбираем сами от полученного уровня значимости, выводимого компьютером.

19