Тест на равенство двух дисперсий. (Критерий Ливиня)

Дисперсионный анализ – достаточно большой раздел статистики. Здесь мы не будем останавливаться на нем подробно, а лишь в общих чертах опишем F-критерий, который используется для проверки гипотезы о равенстве дисперсий. Он вычисляется по следующей формул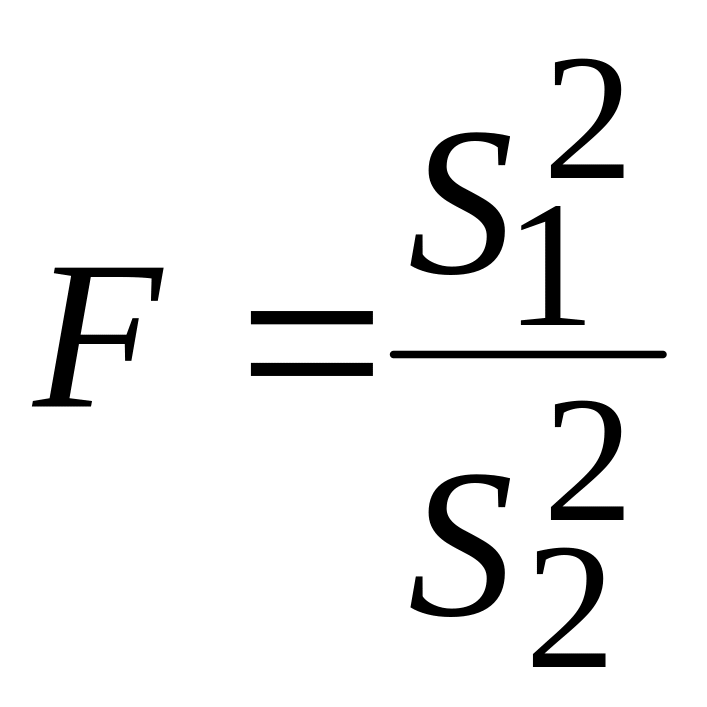е: , где – большая выборочная дисперсия, а – меньшая, а рассчитывается так: .

Проверяемая (нулевая) гипотеза: сравниваемые выборочные дисперсии характеризуют вариацию признака в совокупностях, взятых из нормально распределенных генеральных совокупностей с одинаковыми дисперсиями .

Для того чтобы отвергнуть или принять проверяемую нами гипотезу, мы пользуемся F-распределением Фишера и соответствующими таблицами. В этих таблицах указываются предельные значения F-критерия для различных комбинаций числа степеней свободы числителя и знаменателя, которые могут быть превзойдены с вероятностью 0,05 или 0,01. Число степеней свободы , соответствующее большей дисперсии ( ) определяет столбец таблицы, число степеней свободы ( ) соответствующее дисперсии , строку таблицы (см. приложение: таблица №1).

Рассчитанная по фактическим данным величина дисперсионного отношения сопоставляется с соответствующей данному сочетанию числа степеней свободы числителя и знаменателя и принятому уровню значимости табличной величиной дисперсионного отношения.

Если фактическое дисперсионное отношение будет больше табличного, то лишь с вероятностью 0,05 или 0,01 можно утверждать, что различие между дисперсиями определяется случайными факторами. Иными словами, при фактическом F-критерии превышающем табличный мы отвергаем нулевую гипотезу и считаем, что выборочные дисперсии взяты из генеральных совокупностей с различными дисперсиями.

Допустим, , а ; . Тогда 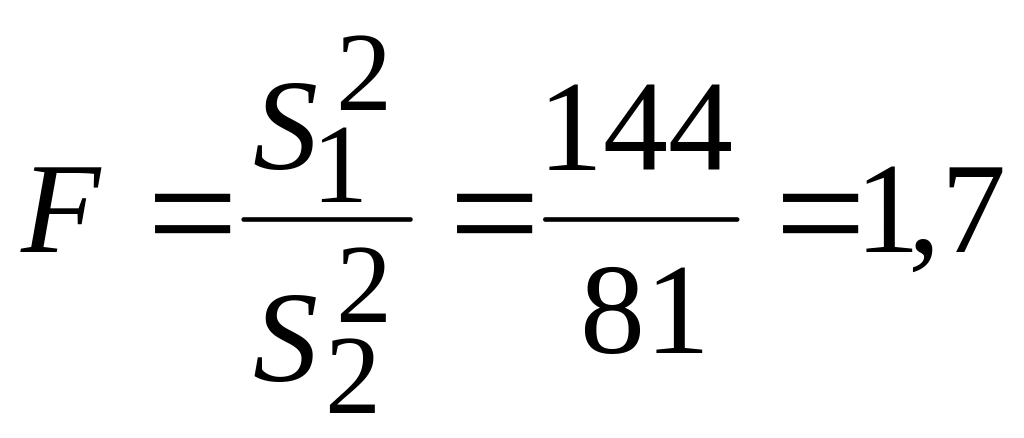, при уровне значимости =0,05. Значит, мы принимаем нулевую гипотезу и считаем дисперсии равными, так как . То есть, несмотря на видимое различие между и , статистически это различие не значимо.

Выбор критерия

На основе сказанного в пунктах 2 и 3, мы выбираем критерий для проверки выдвинутой нами гипотезы. Вернемся опять к нашим примерам (см. таблицу №1). Для проверки гипотезы из первого примера мы воспользуемся t-критерием (каким именно t-критерием, мы здесь считать не будем), для проверки гипотезы из третьего примера мы воспользуемся z-критерием для независимых выборок, для проверки гипотезы из второго примера мы воспользуемся z-критерием для парных выборок.

Уровень значимости и определение области допустимых значений

Уровень значимости – вероятность ошибочно отвергнуть основную проверяемую гипотезу, когда она верна. В социологии обычно используется уровень значимости , , а₂. Критическую область для любого уровня значимости можно найти в таблице: если мы пользуемся z-критерием, то это будет таблица для стандартизированного нормального распределения (см. приложение: таблица №2), если мы пользуемся t-критерием, то это будет таблица для распределения Стьюдента (см. приложение: таблица №3). Приведем более конкретный пример – для начала поговорим о нормальном распределении, а потом о распределении Стьюдента.

Нормальное распределение. Возьмем уровень значимости . На графике критическая область будет выглядеть следующим образом.