Системы связи / Модель_динамич_хаоса

4. Модели динамического хаоса

4.1. Введение

В начале 70-х годов прошлого века при исследовании внешне не сложных детерминированных моделей было обнаружено поведение скорее свойственное стохастическим моделям. Исследование этих моделей привело к появлению нового класса моделей – моделей динамического хаоса.

Для моделей динамического хаоса характерно что предсказать поведение модели на длительный период невозможно. Причем данное свойство проявляется даже у сравнительно простых с точки зрения структуры модели систем различной природы – технических, химических, биологических, социальных, экономических и многих других.

Формально, подобные модели должны быть отнесены к детерминированным моделям. Зная состояние модели в конкретный момент времени можно предсказать ее поведение на протяжении небольшого интервала. На значительных интервалах времени система ведет себя как хаотическая модель.

Процессы в хаотических моделях имеют вид не регулярных колебаний в которой происходит изменения частоты, амплитуды и фазы колебаний.

Модели с подобным поведением стали называть странными аттректорами. Данный класс моделей был открыт американским метеорологом Эдвардом Лоренцом в 1963 г.

Хаотической называется система у которой есть хотя бы один странный аттрактор. Аттрактор называется странным если он ограничен и любая траектория начинающаяся на нем неустойчива по Ляпунову.

Причина появления хаотических движений является нелинейная природа, свойства неустойчивости и непредсказуемости на большой период времени. Неустойчивость по Ляпунову характеризует основное свойство хаотически движений – сверхчувствительности от начальных значений: две сколь угодно близкие траектории обязательно разойдутся на конечное расстояние.

Хаотическая траектория полностью воспроизводится если воспроизвести точно такие же начальные условия.

Изучение подобных моделей показали что в природе существует только несколько сценариев перехода к хаотическому поведению. Любая сложная нелинейная система обязательно в процессе своего развития проходит через этапы хаотического поведения.

Находясь на периоде хаотического поведения целевая функция системы не теряется, а пытается уловить новое направление поведения, совпадающие с направлением потенциального пути развития системы.

4.2. Модели систем динамического хаоса

Маятник с возбуждающей силой

Уравнение маятника, к которому приложена возбуждающая сила можно описать в виде

,

где – угол отклонения маятника, – возбуждающая сила.

Обозначив координаты описывающие модель в виде:

,

получим следующий вид модели, результаты численного моделирования которой показаны на рис. 4.1.

.

а

б

Рис.4.1. Результаты моделирования маятника с возбуждающий силой

а – график и , б – фазовая траектория для

Зависимость угла отклонения от времени показанная на рис. 4.1.а выглядит хаотическим.

Странный аттрактор Лоренца

Модель странного аттрактора Лоренца является одной из самых необычных моделей нелинейной динамики.

График поведения модели и фазовая траектория, для начальных условий , показаны на рис. 4.2.

а

б

Рис. 4.2. График и фазовые траектории странного аттрактора Лоренца

Цепь Чуа

Цепь Чуа была предложена в 1982 г. Схема содержала всего один нелинейный элемент, но оказалась способна генерировать хаотические колебания. Вид схемы Чуа приведен на рис. 4.3. Математическая модель цепи Чуа имеет вид:

,

где .

Рис. 4.3. Цепь Чуа

При значениях параметров , , , траектория системы демонстрируют хаотическое поведение, показанное на рис. 4.4.

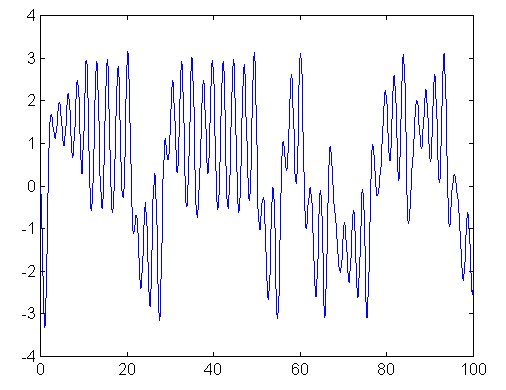
а

б

Рис. 4.4. Траектория процессов в цепи Чуа

Уравнение Дуффинга

Уравнение Дуффинга описывает систему 2-го порядка с нерегулярными колебаниями. Модель системы описывается следующим образом:

.

Для получения хаотических процессов рекомендуется взять следующие параметры: , , , .

Для численного моделирования в пакете MatLab Вам необходимо преобразовать модель к нормальной форме Коши:

.

Внешний вид процессов показан на рис. 4.5.

а

б

Рис. 4.5. Вид процессов в модели Дуффинга

Система Росслера

Система Росслера описывается системой уравнений вида:

,

рекомендуемые параметры для моделирования: , , .

Внешний вид процессов приведен на рис. 4.6.

а

б

Рис. 4.5. Вид процессов в системе Росслера

Модель забастовочного движении

Модель забастовочного движения была предложена А.Ю. Андреевым и М.И. Левандовским. Как показали результаты вычислительного эксперимента модель дает адекватное описание стачечного движения во Владимирской области с 1895 по 1905 года.

Модель имеет вид:

,

где – общее число рабочих, – число рабочих не получивших информацию о стачке, – рабочие согласившиеся участвовать в забастовке, но не ведущих активной агитации, – число активных агитаторов, – число рабочих отказавшихся участвовать в забастовке.

Модель химической реакции типа диффузии

Модель описывается системой уравнений вида:

,

рекомендованные значении , , .

4.3. Использование хаотических моделей

Модели динамического хаоса используются для описания целого ряда процессов и устройств для которых характерно наличие не регулярных колебаний. В качестве примеров таких устройств можно привести:

• газовые и полупроводниковые лазеры в моногомодовых режимах;

• механические системы с люфтами и ударами;

• механические системы состоящие из нескольких колебательных систем;

• электронные схемы с туннельными диодами или подобными активными элементами;

• химические процессы с нелинейной кинетикой;

• экономические процессы, например бизнес–циклы.

Хаотические модели можно использовать для генерации нерегулярных и псевдослучайных сигналов. В частности подобные сигналы можно использовать в качестве несущей для передачи информации. Две хаотические системы можно заставить синхронно колебаться, что позволяет использовать их в качестве генератора несущего сигнала, который для перехватывающего его противника по своим характеристикам будет соответствовать случайному процессу.

9