Системы связи / теория кодирования

4. Основы теории кодирования

4.1. Классификация кодов

Под кодированием (рис. 4.1) понимается преобразование , где сообщению ставится один или несколько символов . Преобразование должно обеспечивать однозначность операции кодирования и декодирования соответственно . Как правило, на практике, , например символ русского языка , кодируемый в ЭВМ двоичным кодом .

Рис. 4.1. Иллюстрация процесса кодирования

Классификация кодов приведена на рис. 4.2.

Рис. 4.2. Классификация кодов

Экономное кодирование. В основе экономного кодирования лежит минимизация избыточности сообщения , и на основании этого повысить эффективность передачи информации по каналам связи.

Помехоустойчивое кодирование предполагает внесение избыточности в исходное сообщение, за счет которой возможно выявление (исправление) ошибки возникшей при передаче по каналам связи.

Как правило, помехоустойчивое кодирование сочетается с экономным кодированием.

Рис. 4.3. Использование экономного и помехоустойчивого кодирования

В системе связи, показанной на рис. 4.3, в которой исходное сообщения в начале кодируется экономным способом, с целью минимизации избыточности, после чего символы кодируются помехоустойчивым кодом. Полученные сообщения посылаются в канал связи.

Помехоустойчивые коды можно разделить на:

обнаружающие – в обнаружающих кодах, за счет избыточности сообщение возможно распознать появление ошибки и дать запрос на повторную посылку сообщения (рис. 4.4);

исправляющие – исправляющие коды, за счет заложенной избыточности позволяют исправить определенное количество ошибок в сообщении.

Рис. 4.4. Иллюстрация принципа работы обнаруживающих кодов

Кроме того, все коды можно разделить на блочные и непрерывные (рис. 4.5).

Рис. 4.5. Блочные и непрерывные коды

Непрерывные коды – исходной последовательности ставится в соответствие последовательность не разделенную на отдельные кодовые комбинации. Например, в процессе передачи исходное сообщение переводится на английский язык, кодирование в этом случае производится не виде замены символов исходного алфавита, а замены сообщения (предложения) созданного в алфавите эквивалентного по содержанию сообщения построенного в алфавите .

Блочные коды – каждому символу исходного сообщения ставится последовательность .

Блочные коды разделяют на:

Равномерные блочные коды – все кодовые последовательности имеют одинаковую длину – символов. Наиболее яркий пример, кодовая таблица ASCII, для кодирования каждого символа выделяется 8 бит ().

Неравномерные блочные коды – последовательность имеет различную длину для разных символов исходного сообщения. Например, азбука Морзе, где символы кодируются комбинацией точек и тире (), но длительность их различная. Часто встречающиеся символы кодируется точкой, тире или двух символьной комбинацией точек и тире. Редко встречающийся символ, например, твердый знак – кодируется девятью символами точек и тире.

На практике в основном используются равномерные блочные коды.

Для однозначности процесса кодирования и декодирования, необходимо чтобы

,

где – количество символов исходного алфавита, – количество символов вторичного алфавита (после кодирования), – длина кодовой последовательности.

Избыточность кода можно оценить как:

.

Будем считать алфавиты первичного и закодированного сообщения составленного из чисел позиционных систем счисления.

Для любой позиционной системы счисления по основанию можно записать следующим образом:

.

Например, десятичное число в коде по основанию , будет выглядеть следующим образом . В этом не трудно убедится, если перевести это значение в код по основанию десять: .

Представление самолов исходного алфавита в различных позиционных кодов приведено в табл. 4.1.

Таблица 4.1. Представление символов в различных позиционных кодах

Символ	Коды
А	00	0	00	00	0000
Б	01	1	01	01	0001
В	02	2	02	02	0010
Г	03	3	03	03	0011
Д	04	4	04	10	0100
Е	05	5	05	11	0101
Ж	06	6	06	12	0110
З	07	7	07	13	0111
Е	08	8	10	20	1000
И	09	9	11	21	1001
К	10	А	12	22	1010
Л	11	B	13	23	1011
М	12	C	14	30	1100
Н	13	D	15	31	1101
	0,4430	0,0749	0,3833	0,0749	0,0749

Кроме табличных форм представления кодов используются и деревья, примеры которых приведены на рис. 4.6.

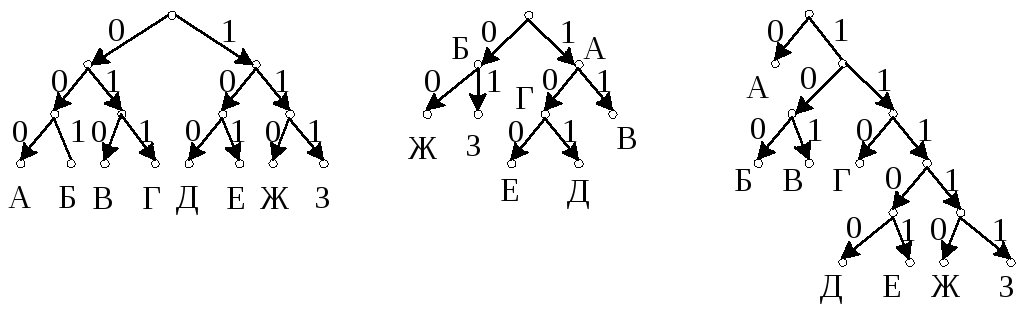
а) б) в)

Рис. 4.6. Кодовые деревья а) – равномерный код; б) – неравномерный приводимый код; в) – неравномерный неприводимый год

На рис. 4.6.а представлен равномерный бинарный код длиной 3 двоичных символа. На рис. 4.6.б представлен не равномерный код, каждой букве в нем соответствует уже не вершины, а все узлы дерева. Однако данный способ может вызвать неоднозначность декодирования. На рис. 4.6.в приведен неравномерный код, позволяющий однозначно кодировать и декодировать сообщения. Значения этих кодов приведены в табл. 4.2.

Таблица 4.2. Бинарные коды, соответствующие рис. 4.6

Символ	Вероятность	Бинарный код, соответствующий рис.
		Рис. 4.6.а	Рис. 4.6.б	Рис.4.6.в
А	0,48	000	1	0
Б	0,25	001	0	100
В	0,12	010	11	101
Г	0,06	011	10	110
Д	0,04	100	01	11100
Е	0,02	101	00	11101
Ж	0,02	110	100	11110
З	0,01	111	101	11111
		3	1,30	2,22

Эффективность неравномерного кодирования может быть значительно выше, если учитывать разную вероятность появления символов в исходном сообщении . Для примера в табл. 4.2 приведены значения для гипотетического источника.

Средняя длина кодовой комбинации может быть получена по формуле

, (4.1)

где – длина кодовой комбинации соответствующей символу.

Минимально возможное среднее значение длины кодовой последовательности, по формуле К. Шеннона равно

,

для приведенных в табл. 4.2 значений . Значение для неравномерного приводимого кода (рис.4.6) меньше этой величины, вследствие неоднозначности кодирования.

4.2. Корректирующие коды

Коррекцию ошибок возможно организовать только за счет избыточности заложенной в коды. Те есть для всех корректирующих кодов

,

где – объем алфавита кодирующего устройства, – длина кода, – количество символов алфавита исходного сообщения.

Рис. 4.7. Структура системы связи

Если источник сообщений выдает символы , во время кодирования в блочный год они преобразуются в символы . Предполагается что вторичный код обладает избыточностью, те есть , где – длина кодовой последовательности.

После передачи сообщения по каналам связи возможно появление ошибки, и получатель примет сообщение , декодируемое в сообщения . Алфавит получателя сообщений, вследствие влияния ошибки и избыточности кода, будет больше, чем алфавит кодирующего устройства .

Все последовательности символов можно рассмотреть как , соответствующие передаваемые источником сообщений и сообщения , соответствующие недопустимым символам. Прием таких кодовых последовательностей можно воспринимать как признак ошибки.

В системах с исправлением ошибок все недопустимые последовательности разбиваются на непересекающиеся подмножества, каждое из которых приписывается наиболее близкому символу исходного сообщения или, если распознать переданный символ не удалось, то признаку ошибки. Анализ последовательностей на предмет возможного соответствия символам производится заранее, и, как правило, в реализациях подобных систем записывается в ПЗУ, из которого декодер только извлекает нудный символ.

Пример декодирования сообщений с ошибками праведен в табл. 4.3. Алфавит исходного сообщения состоит из двух символов , которые кодируется последовательностями . Символ ‘?’ в таблице означает, что приемнику не удалось распознать передаваемый символ.

Для оценки различий в последовательностях кодовых символов используется расстояние по Хеменгу

. (4.2)

Таблица 4.3. Пример декодирования сообщений принятых с ошибками

Передаваемый символ	А	А	Б	Б	А	А	Б	Б
Передаваемая последовательность	000	000	111	111	000	000	111	111
Принятая последовательность	000	?00	001	0?0	111	0??	101	???
Расстояние по Хеменгу по нестертым позициям	0	0	2	2	3	0	1	–
Декодированный символ	А	А	А ош.	А ош.	Б ош.	А	Б	–

Важную роль играет минимальное расстояние между разрешенными кодовыми комбинациями кода. Для приведенного в табл.4.3 кода .

Блочный код позволяет исправить ошибок.

Максимальное количество исправляемых символов , максимальное количество обнаруживаемых ошибок .

В общем случае блочный код с расстоянием позволяет исправить ошибок и стираний, обнаружить ошибок:

.

Линейные коды

Большое распространение на практике получили линейные коды. Линейным двоичным кодом называется код, для которого сумма по модулю двух любых разрешенных кодовых комбинаций является разрешенной кодовой комбинацией.

Линейный код является систематическим, если символов его являются информационными, а символов являются проверочными (– длина кодовой последовательности).

Линейный код обозначают и его можно записать как:

Избыточность линейного кода определяется как:

.

Для примера рассмотрим код (8,4), проверочные символы которого формируются следующим образом:

.

Например, при передаче символа , кодовая последовательность будет иметь значение: .

Получатель сообщения примет последовательность . Вследствие ошибки в канале, принятая последовательность может отличаться от переданной последовательности: . В этом случае выбирается комбинация наиболее близкая по расстоянию по Хеменгу (4.2) из числа всех возможных комбинациях.

Например, при передаче рассмотренной выше последовательности возникли ошибки, результаты сравнения приведены в табл.4.4.

Табл. 4.4. Пример работы линейного кода (8,4)

Переданная последовательность		0 1 0 0 1 0 1 1	0 1 0 0 1 0 1 1	0 1 0 0 1 0 1 1
Ошибка		0 0 0 0 0 0 0 0	0 0 0 0 0 0 0 1	1 0 0 0 0 0 0 1
Принятая последовательность		0 1 0 0 1 0 1 1	0 1 0 0 1 0 1 0	1 1 0 0 1 0 1 0
Все возможнее комбинации кода		Расстояние по Хеменгу между переданной и принятой последовательностью
0	0 0 0 0 0 0 0 0	4	3	4
1	0 1 1 1 1 0 0 0	4	3	4
2	1 0 1 1 0 1 0 0	8	7	6
3	1 1 0 0 1 1 0 0	4	3	2
4	1 1 0 1 0 0 1 0	4	3	2
5	1 0 1 0 1 0 1 0	4	3	2
6	0 1 1 0 0 1 1 0	4	3	4
7	0 0 0 1 1 1 1 0	4	3	4
8	1 1 1 0 0 0 0 1	4	5	4
9	1 0 0 1 1 0 0 1	4	5	4
10	0 1 0 1 0 1 0 1	4	5	6
11	0 0 1 0 1 1 0 1	4	5	6
12	0 0 1 1 0 0 1 1	4	5	6
13	0 1 0 0 1 0 1 1	0	1	2
14	1 0 0 0 0 1 1 1	4	5	4
15	1 1 1 1 1 1 1 1	4	5	4
Декодирование		Верно	Верно	Невозможно