30. Алгоритм распознавания «Кора 3»

Алгоритм, моделирующий работу коры мозга для распознавания образов, в частности в геологоразведке. Основное его отличие от изученных алгоритмов, основанных на мере сходства (Голотип) и расстоянии (ДФ) между объектами, заключается в том, что здесь нет ни меры сходства ни расстояния, а анализ основывается на частотном составе. Важно! Данный алгоритм ориентирован на ситуацию, когда объектов мало, а свойств много.

1.Исходные данные представляются в виде ТОС шкалы только арифметические. Для каждого объекта материала обучения известно его прямое свойство.

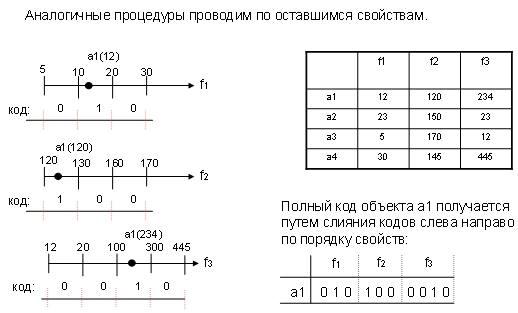
2.Строим гистограммы по свойствам: Для этого, разбиваем диапазон значений свойства (от min к max) на градации (интервалы) Количество интервалов вы выбираете сами по ситуации

Далее наносим на ось все объекты.

3.Производим перекодирование объектов. Суть кодирования заключается в изменении способа описания объекта. К примеру закодируем объект а1: Его значение по первому свойству = 12. Наносим его на ось с интервалами между 10 и 20 (интервал2).

Кодирование происходит по интервалам: Если объект не попал в интервал, то ему присваивается «0», а если попал, то «1». Таким образом, новый код объекта a1 по 1му свойству: а1={010}, вместо старого кода ={12}.Важно отметить, что правила по которым мы перекодируем объекты – чисто эвристические и не являются формально математическими. Поэтому результат напрямую зависит от того на сколько интервалов разбивать то или иное свойство и т.п.

14) Дискриминантная ф.

У равнение гиперплоскости в общем виде можно записать следующим образом:

Э та формула называется уравнением линейной дискриминантной функции, где -- n-мерный вектор столбец в пространстве свойств

Далее, если матрицы различны, рассчитываем усредненную

матрицу ковариации:

22) Алгоритм расп. Голотип 1

Из предназначения алгоритма вытекают три различные постановки задачи:

1. 1) задача распознавания на один образ;

2. 2) Задана совокупность объектов, которую требуется разбить на группы

3. однородных (в некотором смысле) объектов (задача районирования).

4. 3) Задана совокупность объектов, для которой необходимо определить

5. представительность МО.

6. 

Шаг1: Постановка задачи

заносим в ТОС объекты

Шаг4: Рассчитываем матрицы мер сходства для каждого свойства

Ш аг5: Вычисляем общую матрицу мер сходства

m – число свойств в ТОС;

Единственным условием является то , что

Шаг6: Вычисление порога μ₀

для разбиения материала обучения на однородные группы

Используя меру сходства между объектами по общей матрице мер

с ходства, можно выделить из исходной совокупности однородные группы, сравнивая меру сходства пороговым значением μ₀ :

Если условие выполняется, то считаем, что объекты связаны

одной связкой. Если нет, то связка рвется, но это не значит, что объекты

не могут оказаться в одной группе.

В качестве μ_{0 например, выберем среднюю меру сходства}

Шаг7: Построение голотипов и радиусов

Голотип – это тот объект, у которого средняя мера сходства с остальными объектами данной группы является максимальной, т.е. тот на который все остальные объекты в группе наиболее похожи.

m – количество объектов в группе

Шаг8: Построение радиусов Радиусом однородной группы является мера сходства голотипа с самым удаленным объектом однородной группы.

На этом заканчивается процесс обучения и начинается процесс экзамена! Распознавание объекта «x» производится в соответствии с 3 типами задач следующим образом: 1. Объект принадлежит образу, если существует голотип, мера сходства которого с x больше соответствующего радиуса, в противном случае x к образу не относится. 2 Для случая исследования материала обучения на представительность для объекта x проводим аналогичные сравнения. МО считается непредставительным для x, если нет ни одного голотипа, мера сходства которого с x больше соответствующего ему радиуса. 3 Для задачи районирования в качестве результата используются все полученные однородные группы.