
Лабораторная № 3
.docФедеральное агентство по образованию РФ
Санкт-Петербургский государственный электротехнический университет
Кафедра МО ЭВМ
Минимизация логических функций на гиперкубах.
Преподаватель: Красюк В.И.
Студент гр. 4351 Кузьменко А.
Санкт-Петербург
2008
Часть 3. Минимизация логических функций на гиперкубах.
Одним из методов представления логических функций является графическое представление – гиперкуб. На этом представлении основан один из методов минимизации логических функций.
Введем понятия элемента гиперкуба, элемента функции, основного элемента функции. Для иллюстрации вводимых понятий рассмотрим изображение гиперкуба размерности 4 с обозначенными вершинами:

Каждая вершина этого гиперкуба имеет 4 координаты, например вершина 12 имеет координаты 0,0,1,1, что соответствует двоичному представлению числа 12 (младшие разряды слева).
Элемент гиперкуба – это множество из 2m вершин, обладающих (n-m) равными координатами, где n-размерность гиперкуба, m – размерность элемента гиперкуба, m=0..n.
Рассмотрим элементы гиперкуба разных размерностей (от 0 до 4):
-
m=0, количество вершин Nв= 20= 1 , количество равных координат Nрк = 4 – 0 = 4. Элементами гиперкуба размерности 0 являются вершины гиперкуба, например (12), (5), (0). Всего у 4-мерного гиперкуба N=24=16 вершин.
-
m=1, Nв= 21= 2, Nрк= 4-1= 3. Элементами гиперкуба размерности 1 являются ребра гиперкуба, например (8, 10), (6, 7). Легко убедится, что вершины, входящие в одно ребро, обладают тремя равными координатами. Так, любое ребро гиперкуба направлено вдоль одной из координатных осей. Координаты вершин ребра различаются по этой координатной оси, остальные координаты одинаковы. Например, ребро (8, 10) = (0010, 0110) направлено вдоль оси x2, и разница между вершинами – во второй координате слева. Рассмотрим одну вершину, например 13. Вершины, инцидентные ей – порождающие соседи. Вершина 13 входит в 4 ребра – (5, 13), (9, 13), (12, 13), (13, 15), расположенных вдоль осей x4, x3, x1 и x2 соответственно. Любая вершина гиперкуба входит в
 одноразмерных элементов. Всего в
4-мерном гиперкубе
одноразмерных элементов. Всего в
4-мерном гиперкубе
 ребра.
ребра. -
m=2, Nв= 22= 4, Nрк= 4-2= 2. Элементами гиперкуба размерности 2 являются грани гиперкуба, например (8, 9, 10, 11), (2, 3, 6, 7), (0, 1, 8, 9). Грани расположены вдоль двух координатных осей, поэтому две координаты изменяются, а другие две неизменны, например, грань (8, 9, 10, 11)= (0001, 1001, 0101, 1101) расположена вдоль осей x1 и x2, поэтому координаты 3 и 4 неизменны. Одна вершина (например, 13) входит в
 граней, для n=4
– в 6 граней: (x2,
x3:
13, 15, 9, 11), (x1,
x3:
13, 12, 8, 9), (x1,
x2:
13, 12, 14, 15), (x3,
x4:
13, 9, 5, 1), (x1,
x4:
13, 12, 5, 4), (x2,
x4:
13, 15, 5, 7). Грани называют смежными, если
они имеют общее ребро, например, грани
(13, 12, 8, 9) и (13, 12, 5, 4) – смежные, а (13, 12, 8,
9) и (13, 15, 5, 7) – нет. Каждая вершина
гиперкуба входит в
граней, для n=4
– в 6 граней: (x2,
x3:
13, 15, 9, 11), (x1,
x3:
13, 12, 8, 9), (x1,
x2:
13, 12, 14, 15), (x3,
x4:
13, 9, 5, 1), (x1,
x4:
13, 12, 5, 4), (x2,
x4:
13, 15, 5, 7). Грани называют смежными, если
они имеют общее ребро, например, грани
(13, 12, 8, 9) и (13, 12, 5, 4) – смежные, а (13, 12, 8,
9) и (13, 15, 5, 7) – нет. Каждая вершина
гиперкуба входит в
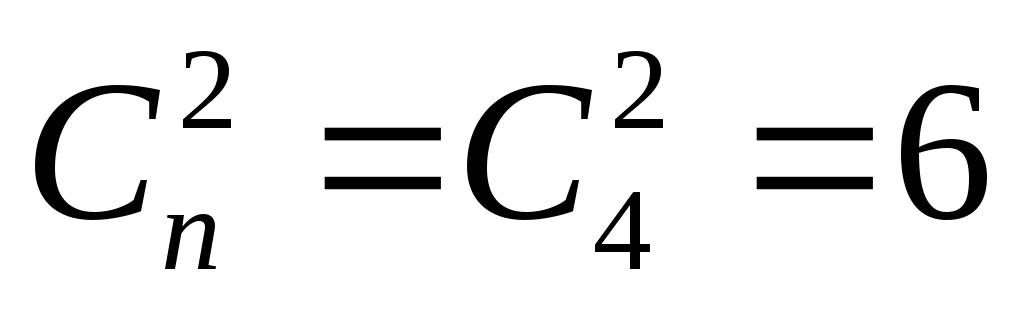 граней, а всего в гиперкубе
граней, а всего в гиперкубе
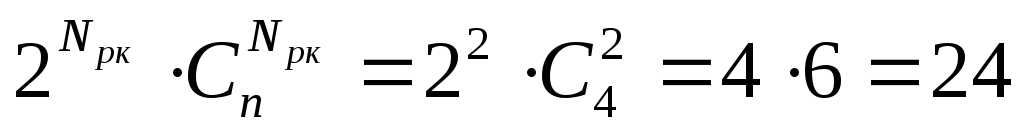 грани.
грани. -
m=3, Nв= 23= 8, Nрк= 4-3 = 1. Элементами гиперкуба размерности 3 являются кубы (подкубы), например (0, 1, 2, 3, 4, 5, 6, 7), (4, 5, 6, 7, 12, 13. 14, 15). Подкубы размерности 3 расположены на 3-х координатных осях, поэтому 1 координата для вершин подкуба неизменна, а три меняется. Так для подкуба (1, 3, 5, 7, 9, 11, 13, 15) первая координата равна 1, а остальные изменяются, для подкуба (4, 5, 6, 7, 12, 13, 14, 15) неизменна третья координата, то есть в него входят вершины двоичным представлением хх1х, где х=0|1. Каждая вершина гиперкуба входит в
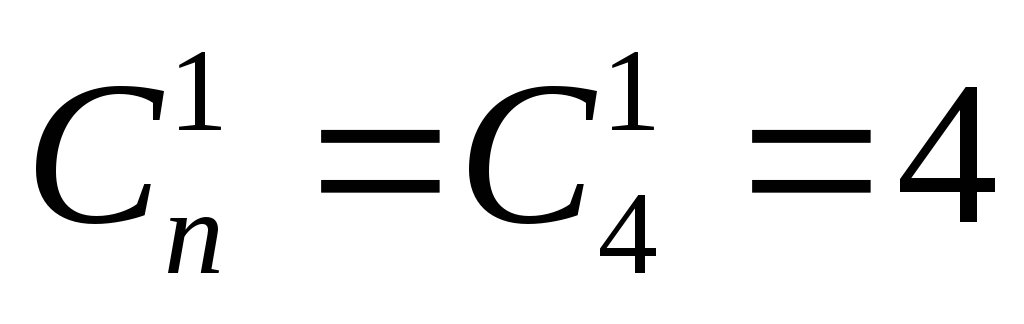 подкубов размерности 3, а всего в
гиперкубе
подкубов размерности 3, а всего в
гиперкубе
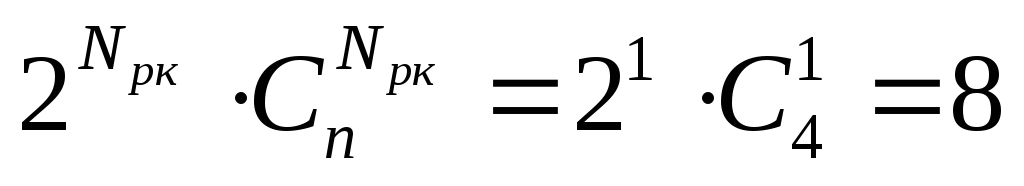 подкубов
размерности 3.
подкубов
размерности 3. -
m=4, Nв= 24= 16, Nрк= 4-4 = 0. Элементом гиперкуба размерности 4 является подкуб размерности 4, то есть сам гиперкуб.
Элементом функции называют такой элемент гиперкуба, что все входящие в него вершины являются элементами множества Т (множества вершин гиперкуба, задающих функцию).
Например если на 4-мерном гиперкубе задана функция Т=(2, 3, 5, 7, 13, 14, 15), то элементами этой функции будут следующие элементы гиперкуба:
- вершины: (2), (3), (5), (7), (13), (14), (15);
- ребра: (2, 3), (3, 7), (5, 7), (5, 13), (7, 15), (13, 15), (14, 15);
- грани: (5, 7, 13, 15).
Подкубы не являются элементами этой функции.
Основным элементом функции называют элемент функции, который не является подмножеством никакого другого элемента функции. Так для приведенного примера основными являются следующие элементы функции: (2, 3), (3, 7), (14, 15), (5, 7, 13, 15), так как все вершины входят в ребра, а ребра (5, 7), (5, 13), (7, 15), (13, 15) входят в грань (5, 7, 13, 15).
Минимальной формой, полученной из гиперкуба, является приведенная система основных элементов функций. То есть система не должна содержать элементов, все вершины которых входят в систему в составе других элементов. Например, если в систему входят ребра (2, 3), (5, 7) и (3, 7), то ребро (3, 7) точно не войдет в приведенную систему, так как вершина 3 входит в ребро (2, 3), а вершина 7 – в ребро (5, 7).
Можно провести определенную параллель между методами минимизации логических функций методами Квайна-МакКласки и на гиперкубах. Так, вершины гиперкуба – конституэнты единицы, элемент функции размерности k – это импликанта k-того уровня, основной элемент функции – это простая импликанта.
Поэтому для приведения системы (основных функций) можно использовать импликантную матрицу, предназначенную для приведения системы простых импликант. Ее столбцами являются конституэнты единицы (вершины), строками – простые импликанты (основные элементы). В ячейках ставится знак, если простая импликанта строки покрывает конституэнту единицы столбца (вершина столбца входит в основной элемент строки). Для приведения системы необходимо
-
найти столбец с единственным знаком (не вычеркнутым),
-
вычеркнуть строку, в которой поставлен этот знак,
-
вычеркнуть столбцы, в которых поставлены знаки в вычеркнутой строке,
-
если зачеркнуты не все знаки (столбцы), начать с п.1.
Тогда основные элементы зачеркнутых строк войдут в приведенную систему.
Для примера, приведенного выше, получим следующую импликантную матрицу (единственные в столбце элементы выделены знаком , в последнем столбце номерами отображен порядок зачеркивания строк):







|
|
2 |
3 |
5 |
7 |
13 |
14 |
15 |
|
|
|
( |
|
х |
|
|
|
|
|
|
1 |
|
(3, 7) |
|
х |
|
х |
|
|
|
|
|
|
( |
|
|
|
|
|
|
х |
|
3 |
|
( |
|
|
|
х |
х |
|
х |
|
2 |
Таким образом,
минимальной формой будет система (2, 3),
(14, 15), (5, 7, 13, 15), или (0100, 1100), (0111, 1111), (1010,
1110, 1011, 1111), или х100, х111, 1х1х, что соответствует
импликантам
![]() .
Таким образом получили минимальную
форму функции
.
Таким образом получили минимальную
форму функции
![]() .
.
В приведенном примере количество конституэнт единицы невелико, поэтому нахождение элементов функции и выделение основных элементов не представляет труда, однако для более сложных функций требуется уточнение (алгоритмизация) этих процедур.
Введем понятие опорной вершины гиперкуба (J*) – элемента функции размерности 0, относительно которого будем искать остальные элементы функции.
Для нахождения
ребер гиперкуба, в которые входит опорная
вершина, необходимо учитывать, что все
вершины, инцидентные опорной, должны
удовлетворять соотношению
![]() ,
где j
- координата, по которой вершина инцидентна
опорной вершине. Из этого соотношения
получаем
,
где j
- координата, по которой вершина инцидентна
опорной вершине. Из этого соотношения
получаем
![]() ,
или
,
или
![]() ,
где хj
– j-тая
координата опорной вершины.
,
где хj
– j-тая
координата опорной вершины.
После нахождения всех Jj для опорной вершины необходимо отсеять вершины, не входящие в рассматриваемую функцию и построить элементы функции размерности 1, в которые входит опорная вершина.
Для нахождения
элементов функции размерности 2 при
наличии более чем одного ребра, необходимо
найти диагональные вершины по координатам
j
и k
относительно опорной вершины - Jjk
, причем
для этого на предыдущем шаге должны
были быть оставлены вершины Jj
и Jk
. Должно соблюдаться соотношение
![]() ,
откуда следует формула
,
откуда следует формула
![]() .
.
Для нахождения
вершины Jjkl
необходимо,
чтобы были 3 попарно смежные грани Jjk,
Jkl,
Jjl,
тогда можно воспользоваться формулой
![]() .
.
Далее можно найти
следующие необходимые вершины по формуле
![]() .
.
На всех шагах необходимо оставлять только элементы функций, из которых после нахождения всех из них, необходимо выделить основные элементы. Для этого надо построить упорядоченный ряд из всех элементов опорной вершины и, просмотрев его, удалить не основные элементы.
Если выбранная опорная вершина не обеспечила покрытие всех вершин функции элементами, в которые она входит, то выбирается следующая опорная вершина из тех вершин, которые не вошли в элементы предыдущей опорной вершины.
Рассмотрим метод минимизации логических функций на гиперкубах на примере функции T = {0, 4, 8, 10, 11, 12, 14, 15, 16, 17, 18, 19, 20, 24, 25, 26, 27, 28}.
Графическое представление:

J* = 0 (00000).
1)
![]() .
.
![]()
![]()
![]()
![]()
![]()
Функция содержит J3=4, J4=8 и J5=16, то получим ребра (0, 4), (0, 8) и (0, 16).
2)
![]() .
.
![]()
![]()
![]()
Функция содержит J34=12, J35=20 и J45=24, то получим грани (0, 4, 8, 12), (0, 4, 16, 20) и (0, 8, 16, 24).
3) Так как грани в
п. 2 попарно смежны, найдем
![]() .
.
![]()
Функция содержит J345=28, то получим подкуб (0, 4, 8, 12, 16, 20, 24, 28).
J* = 0 (01010).
1)
![]() .
.
![]()
![]()
![]()
![]()
![]()
Функция содержит J1=11, J2=8, J3=14, и J5=26, то получим ребра (10, 11), (8, 10), (10, 14) и (10, 26).
2)
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
Функция содержит J13=15, J15=27, J23=12 и J25=24, то получим грани (10, 11, 14, 15), (10, 11, 26, 27), (8, 10, 12, 14) и (8, 10, 24, 26).
3) Так как грани в п. 2 не смежны попарно, то элементов функции размерности больше двух для этой опорной вершины не существует.
J* = 17 (10001).
1)
![]() .
.
![]()
![]()
![]()
![]()
![]()
Функция содержит J1=16, J2=19 и J4=25, то получим ребра (16, 17), (16, 19) и (16, 25).
2)
![]() .
.
![]()
![]()
![]()
Функция содержит J12=18, J14=24 и J24=27, то получим грани (16, 17, 18, 19), (16, 17, 24, 25) и (16, 19, 25, 27).
3) Так как грани в
п. 2 попарно смежны, найдем
![]() .
.
![]()
Функция содержит J124=26, то получим подкуб (16, 17, 18, 19, 24, 25, 26, 27).
Таким образом получим следующие элементы функции:
|
|
|
J* = 0 |
J* = 10 |
J* = 17 |
|
|
0 |
Х |
- |
- |
|
|
4 |
j3 |
- |
- |
|
|
8 |
j4 |
j2 |
- |
|
|
10 |
- |
Х |
- |
|
|
11 |
- |
j1 |
- |
|
|
12 |
j34 |
j23 |
- |
|
|
14 |
- |
j3 |
- |
|
|
15 |
- |
j13 |
- |
|
|
16 |
j5 |
- |
j1 |
|
|
17 |
- |
- |
Х |
|
|
18 |
- |
- |
j12 |
|
|
19 |
- |
- |
j2 |
|
|
20 |
j35 |
- |
- |
|
|
24 |
j45 |
j25 |
j14 |
|
|
25 |
- |
- |
j4 |
|
|
26 |
- |
j5 |
j124 |
|
|
27 |
- |
j15 |
j24 |
|
|
28 |
j345 |
- |
- |
Выделим основные элементы функции:
J*
= 0 (00000) – (j345,
j34,
j35,
j45,
j3
, j4,
j5)
– основной элемент - j345
(![]() );
);
J*
= 10 (01010) – (j23,
j13,
j25,
j15,
j1,
j2,
j3,
j5)
– основные элементы - j23,
j13,
j25,
j15
(![]() );
);
J*
= 17 (10001) – (j124,
j12,
j14,
j24,
j1
, j2,
j4)
- основной элемент – j124
(![]() );
);
Построим неизбыточную систему с помощью импликантной матрицы:
|
|
0 |
4 |
8 |
10 |
11 |
12 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
24 |
25 |
26 |
27 |
28 |
|
|
|
|
х |
х |
|
|
х |
|
|
х |
|
|
|
х |
х |
|
|
|
х |
1 |
|
|
|
|
|
х |
|
|
х |
х |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
х |
х |
|
|
х |
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
х |
|
|
|
|
|
|
|
|
|
|
|
х |
х |
|
|
|
|
|
х |
х |
|
|
|
|
|
|
|
|
|
|
х |
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
х |
|
х |
х |
|
х |
х |
х |
х |
|
3 |
Таким образом
получим МДНФ функции : f=![]()
![]()
![]() .
.
Для проверки построим прямоугольную таблицу истинности найденной функции и сравним ее с таблицей для исходно заданной функции.
Построенная таблица
(для наглядности вместо единиц проставим
номера импликант 1 -
![]() ,
2 -
,
2 -
![]() ,
3 -
,
3 -
![]() ):
):
-
x1
0
1
0
1
0
1
0
1
x
x3
20
0
1
1
0
0
1
1
x
x5
4
0
0
0
0
1
1
1
1
0
0
1
0
0
0
1
0
0
0
1
0
1
0
3
3
1
0
3
3
0
1
1 2
2
2
2
1
0
0
0
1
1
1 2
2
2
2
1
0
0
0

 2,
3)
2,
3) 14,
15)
14,
15) 5,
7, 13, 15)
5,
7, 13, 15)