Особенности моделирования источника и приемника излучения

С учетом принятых допущений структура модели примет вид, представленный на рисунке 3:

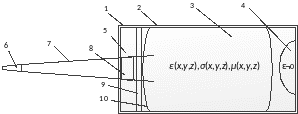
Рисунок 3. 1 – объем расчетной области, 2 – поглощающий слой UPML, 3 – плазма установки, 4 – абсолютно отражающий слой, 5 – вакуум (ε = 1), 6 – действительный источник зондирующего СВЧ излучения (антенна ИРР), 7 – границы пучка СВЧ излучения, 8 – мнимый источник СВЧ излучения, 9 – область определения времени пролета отраженной от плазмы зондирующей волны, 10 – внешняя граница плазмы

Моделирование происходит в объеме расчетной области 1 Рисунка 3, соответствующего границам расчетного объема, отмеченного на Рисунке 1. Для ускорения расчетов, источник электромагнитного излучения 6, реально расположенный вне области моделирования, заменяется мнимым источником излучения 8, расположенным на границе основной расчетной области, как схематично показано на рисунке 3. Мнимый источник задается в объеме перед плазменным образованием, границы пучка подбираются с учетом апертуры излучающей антенны, частотных характеристик и распределения мощности излучения.

Расчет времени пролета по модели может быть осуществлен при анализе пространственно-временного распределения поля только в крайнем, по направлению к приемной антенне, слое основного расчетного объема (см. Рисунок 3), а не во всем расчетном объеме. Можно заранее установить какие распределения мощности отраженного излучения в этом слое будут приводить к попаданию отраженного излучения в приемную антенну и превышению порогового уровня мощности детектирования времени пролета. Напомним, что процесс распространения отраженного излучения от границы плазмы в приемную антенну и его детектирование для упрощения считаются детерминированными, поэтому добавка к времени пролета на этом участке будет постоянной величиной, а определение времени пролета по модели сведется к распознаванию приемлемого распределения мощности излучения на границе плазмы и фиксации времени его появления, относительно известного момента испускания зондирующего излучения.

Представленная модель может использоваться не только для моделирования времени пролета зондирующего излучения в плазме. Например, можно исследовать динамику распространения электромагнитного поля в основном расчетном объеме, если ставятся такие цели моделирования. Однако стоит отметить, что при таком подходе возникнут проблемы сохранения больших объемов результатов моделирования на жестком диске и проблемы уменьшения времени расчета, результаты оценки которых приведены в [14]. Поэтому в каждом конкретном случае необходимо искать компромисс между возможностями вычислительной системы и объемом используемой для анализа информации, а также временем расчета.

Заключение

Предлагаемая трехмерная модель позволяет по заданному трехмерному распределению комплексной диэлектрической проницаемости и параметрам пучка зондирующего электромагнитного излучения, таким как ориентация пучка в пространстве, частота монохроматического излучения, распределение энергии по сечению пучка, длительность и форма огибающей волнового пакета, рассчитывать и сохранять пространственно-временное распределение мощности отраженного излучения в плоскости раскрыва приемной антенны. На основании этой информации может быть легко рассчитано суммарное время пролета зондирующего излучения в плазме и свободном пространстве между плазмой и приемной антенной. Моделирование и интерпретация времени пролета волны в плазме и вакуумной камере является основной целью создания модели, т.к. именно этот параметр экспериментально измеряется по методу импульсной рефлектометрии плазмы на установках УТС.

Данная работа проводилась при финансовой поддержке министерства образования и науки российской федерации

СПИСОК ЛИТЕРАТУРЫ

1. Shevchenko V. F., Walsh M. J., First results from the small tight aspect ratio tokamak multifrequency pulse radar reflectometer, Review of Scientific Instruments. 1997. Т. 68. № 5. С. 2040-2045.

2. Петров В.Г., Петров А.А., Малышев А.Ю. и др. Времяпролетные измерения плотности плазмы на токамаке Т-11М. Физика Плазмы, 2006, том 32, № 4 С. 346-351.

3. Bruskin L.G., Mase A., Conway G.D. Application of astratified plasma model to microwave reflectometry of density fluctuations, PlasmaPhys. Control.Fusion,№47.

4. Yokota, Y. Mase A. KogI Y and other. Simulation Study of Ultrashort-Pulse Reflectometry by Signal Record Analysis. Plasma and Fusion Research, № 3, 008 (2008).

5. Petrov A.A.,Petrov V.G. Time-of-flight refractometry for robust line integral electron density measurements and control in ITER, review of scientific instruments, volume 74, number 3.

6. Pelosi G. The finite-element method, Part I: R. L. Courant, Antennas and Propagation, Volume 49, №2, С. 180 – 182.

7. Taflove A., Umashankar K.R. The Finite-Difference Time-Domain (FD-TD) Method for Electromagnetic Scattering and Interaction Problems, Journal of Electromagnetic Waves and Applications, Vol. 1, № 3, С 243-267.(1987)

8. Yee K. S. Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media, Trans Antennas Propagat, volume AP-14. C. 302-307.

9. TafloveA.HagnessS.Computational Electrodynamics: The Finite-Difference Time-Domain Method, second edition. 852p.

10. J.-P. Berenger, A perfectly matched layer for the absorption of electromagnetic waves, J. Comput. Phys. 114, 185 (1994).

11. Tong M. S., Chen Y. C., Kuzuoglu M., Mittra R. A new anisotropic perfectly matched layer medium for mesh truncation in finite difference time domain analysis, International Journal of Electronics, volume 86, C. 1085-1091. (1999)

12. Marcatili E.A. Bends in optical dielectric guides, Bell System Technical ,Volume 48, C. 1819-1821 (1969)

13. OdaK., TakatoN., Toda H. A wide-FSR waveguide double-ring resonator for optical FDM transmission systems, Lightwave Technology, Volume 9, C. 728-736. (1991)

14. Лобес Л.А., Шарнин А.В., Калашников А.А. Оценка требований к реализации 3D модели импульсной рефлектометриии рефрактометрии плазмы установок типа токамак, Известия Высших учебных заведений, физика. 2011, №11/2, С.98-101.

Поступила в редакцию 10.09.2010 г.

1 Данная работа проводилась при финансовой поддержке министерства образования и науки российской федерации