8.3. Полуэмпирическая теория Прандтля

В настоящее время теория турбулентности представляет достаточно развитый раздел гидромеханики, характеризующийся выдающимися достижениями, однако, общей теории турбулентности до сих пор не построено. Пространственные турбулентные течения, происходящие в различных обстановках, настолько сложны и настолько отличаются друг от друга, что можно говорить лишь о классах таких течений в тех или иных условиях.

Рассмотрим одну из наиболее известных теорий так называемой пристеночной турбулентности, предложенную выдающимся немецким механиком прошлого столетия Л.Прандтлем. Речь идет о турбулентном течении жидкости вблизи жесткой стенки, параллельно ее плоскости. Течение происходит вдоль оси , причем ось направлена вертикально вверх перпендикулярно стенке. Предполагается, что осредненная скорость течения имеет только одну составляющую , а составляющие и равны нулю.

Из уравнения неразрывности (8.15) следует, что в рассматриваемом случае , т.е. составляющая осредненной скорости зависит только от координаты и времени . Если дополнительно принять, что турбулентное течение установившееся в том смысле, осредненные параметры течения в точках пространства не зависят от времени, то , где расстояние до жесткой стенки.

Прандтль предположил, что в турбулентном течении возникают жидкие комки или моли, которые переносят количество движения из слоя в слой через линии тока осредненного движения. Он считал, что жидкий комок, выйдя из слоя, находящегося на некотором расстоянии от данного, сохраняет свое осредненное количество движения, пока не достигнет рассматриваемого слоя и только здесь смешивается с окружающей жидкостью, отдавая ей всю разницу количества движения. Расстояние от слоя, из которого вышел жидкий комок до слоя, где произошло смешение, Прандтль назвал путем смешения .

Пусть один жидкий комок, возникший в слое и обладающий скоростью , переместился на расстояние в направлении, перпендикулярном линиям тока осредненного течения. Поскольку рассматриваемый жидкий комок при перемещении сохраняет свою скорость, то в новом слое он будет иметь скорость меньшую, чем окружающая его жидкость, причем разность этих скоростей пропорциональна градиенту скорости:

. (8.18)

Последнее соотношение получено путем разложения в ряд Тейлора и пренебрежения членами порядка малости выше первого. Эту разность скоростей принимается за пульсационную скорость . Таким образом, Прандтль принял, что . Аналогичную зависимость Прандтль предположил и для пульсационной скорости : , поэтому рейнольдсовская составляющая касательного напряжения была принята Прандтлем в следующем виде:

, (8.19)

где , причем осредненной составляющей сил вязкого касательного напряжения Прандтль пренебрег, считая ее малой по сравнению с количеством движения , переносимым жидкими макро комками.

Примем далее допущение, что величина турбулентного касательное напряжение во всей области течения равно напряжению трения на стенке т. е.

. (8.20)

Здесь и далее, черточки, как обозначение осреднения, отброшены.

Поскольку путь смешения имеет размерность длины, а никакого другого линейного размера, кроме как расстояния до стенки нет, то в модели Прандтля считается пропорциональным этому расстоянию:

, (8.21)

где — безразмерный коэффициент пропорциональности, определяемый из опыта.

С учетом гипотезы Прандтля (8.21) получаем дифференциальное уравнение для скорости :

. (8.22)

Величина имеет размерность скорости, поэтому она обозначается и называется динамической скоростью. С учетом этого обозначения уравнение (8.22) имеет вид:

, . (8.23)

Удобно придать этому уравнению безразмерный вид. Для этого используем имеющиеся размерные параметры. Поскольку , ( кинематическая вязкость жидкости), то уравнение (8.23) можно представить в виде:

, (8.24)

где безразмерное расстояние до стенки.

Интегрируя уравнение (8.24), получаем

, (8.25)

где постоянная интегрирования.

Таким образом, распределение скорости по вертикали от жесткой стенки оказывается не линейным, как при ламинарном течении вязкой жидкости, а логарифмическим (рис.8.4). Формула (8.25) представляет знаменитый логарифмический профиль Прандтля, который блестяще подтверждается экспериментами и в безразмерном виде имеет универсальный вид в том смысле, что не зависит от конкретной рассматриваемой задачи.

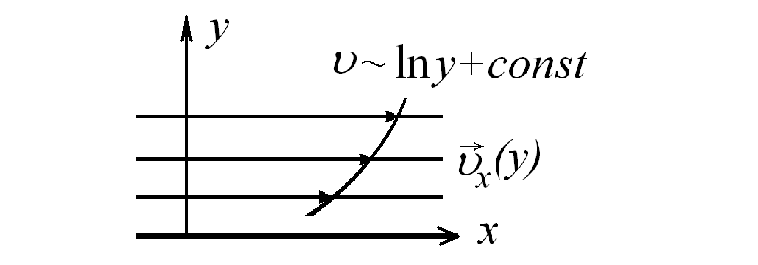
Рис. 8.4. Логарифмический профиль скорости

Вместе с тем, распределение Л.Прандтля имеет определенный недостаток – оно справедливо лишь на некотором удалении от жесткой стенки. Распределение (8.25) не удовлетворяет условию прилипания, согласно которому скорость течения должна обращаться в нуль на самой стенке: из (8.25) следует, что при . Объяснение этого противоречия видят в существовании вблизи жесткой стенки особого тонкого слоя (рис. 8.1), течение в котором описывается другой теорией, отличной от теории Прандтля. Весьма часто принимают, что течение в этом слое – ламинарное, из-за чего сам слой называют ламинарным подслоем. Считают, что распределение скоростей в этом слое линейное, и затем сопрягают его с логарифмическим профилем Л. Прандтля. Область течения обычно разбивают на две области: тонкую пристеночную область чисто вязкого течения (ламинарный подслой) и область развитого турбулентного течения (турбулентное ядро). Между вязким подслоем и турбулентным ядром вводят один, а иногда и несколько, других слоев, в которых учитывают турбулентное и вязкое молекулярное трение [ ].

Сопоставляя результаты опытов по измерению скоростей в сечении трубы с формулой (8.25), И.И. Никурадзе получил, что

.

Константу называют константой Кармана.

Таким образом, логарифмическое распределение скорости в пристеночном турбулентном течении имеет вид:

. (8.26)

Распределение (8.26) позволяет, в частности, вычислить силу трения жидкости о поверхность стенки. Допустим, известна скорость жидкости, набегающей на плоскую стенку, т.е. известна скорость жидкости, текущей вдоль этой стенки, так что на некотором расстоянии от нее скорость равна . Спрашивается, каково касательное напряжение на стенке.

Введем коэффициент гидравлического трения согласно формуле:

или ,

где . На основании формулы (8.26) имеем:

или

,

где число Рейнольдса в турбулентном пограничном слое вблизи стенки. Таким образом, имеем трансцендентное уравнение для определения коэффициента :

. (8.27)

Пример. Вязкая жидкость ( ) набегает на плоскую пластину, так что на расстоянии мм от нее скорость жидкости равна . Определить касательное напряжение на пластине.

Решение. Вычисляем число Рейнольдса:

.

При таких значениях числа Рейнольдса течение в слое вблизи пластины можно считать турбулентным.

На основании (8.27) имеем

.

Решив это уравнение методом последовательных приближений, найдем: , следовательно:

Па.

Ответ: 165 Па.

Если речь идет о течении жидкости в круглой трубе с радиусом и длиной , то имеют место следующие соотношения:

или

,

где разность давлений на концах трубы. Учитывая формулу Дарси-Вейсбаха, согласно которой , получаем связь динамической скорости со средней по сечению скоростью жидкости в трубе:

. (8.28)

Иными словами, отношение равно . Поскольку , то , следовательно, динамическая скорость составляет 3-6% от средней скорости.

(8.36) следует положить . Тогда распределение скорости запишется в виде:

. (8.37)

Если положить и , то закон распределения скоростей (8.37) Т.Кармана совпадает с соответствующим распределением (8.26) Л.Прандтля.