7. Ламинарное течение несжимаемой жидкости в круглой трубе

Рассмотрим установившееся ламинарное течение несжимаемой жидкости в круглой трубе, линиями тока которого будут прямые, параллельные оси и образующим стенки трубы. Направим ось ОХ по оси трубы, так что поперечное сечение трубы лежит в плоскости . Тогда и остается лишь одна отличная от нуля компонента скорости . Из уравнения неразрывности (5.4) следует, что

,

т. е. компонента не зависит от , а является функцией лишь и . Однако вследствие радиальной симметрии течения функция определяется не самими координатами и , а лишь их комбинацией , являющейся расстоянием точки сечения трубы от ее оси: .

Связь касательного напряжения между слоями жидкости и разностью скоростей этих слоев, рассчитанной на единицу расстояния между ними (градиентом скорости) в общем случае можно записать как

. (7.1)

Для различных жидкостей эта связь может иметь различный вид, однако, отметим два частных случая, имеющих, однако, широкое применение в практике.

1. Функция 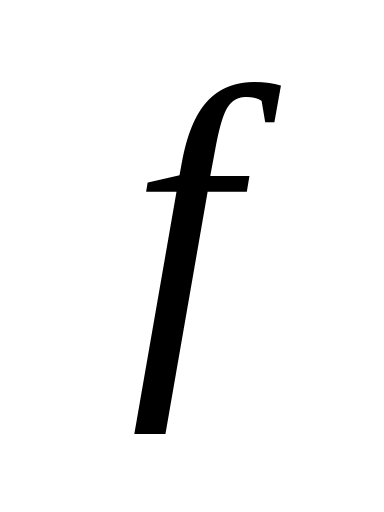есть линейная функция своего аргумента, причем :

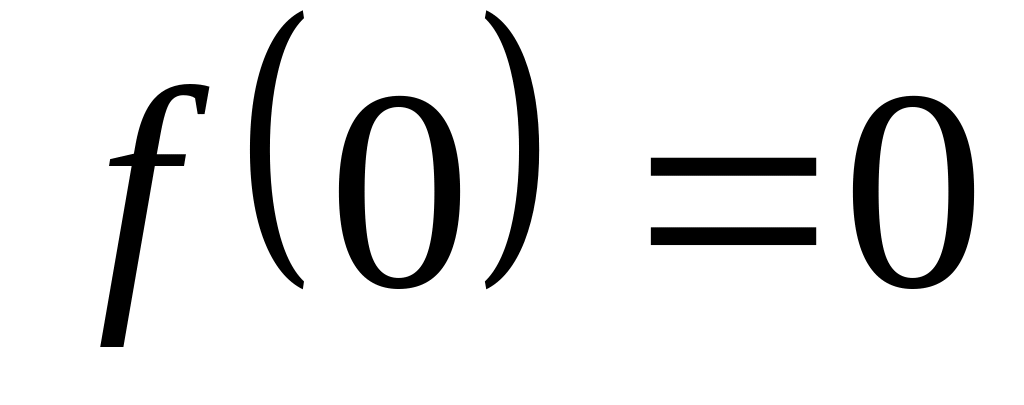. (7.2)

Жидкость, удовлетворяющую реологическому соотношению (7.2), называют ньютоновской вязкой жидкостью, а коэффициент пропорциональности - динамической вязкостью этой жидкости. Очевидно, что размерность , причем в системе СИ единицей измерения динамической вязкости служит величина , называемая одним Пуазом: .

Условие означает, что при отсутствии скорости движения слоев жидкости друг относительно друга (скорости сдвига) касательное напряжение между слоями равно нулю.

Поскольку слои жидкости, расположенные ближе к оси трубы, движутся быстрей, чем слои жидкости, расположенные дальше от нее, , следовательно, , т.е. медленные слои тормозят быстрые. Если вместо касательного напряжения ввести его модуль , который в рассматриваемом случае равен , то формула (7.2) приобретет вид:

(7.3)

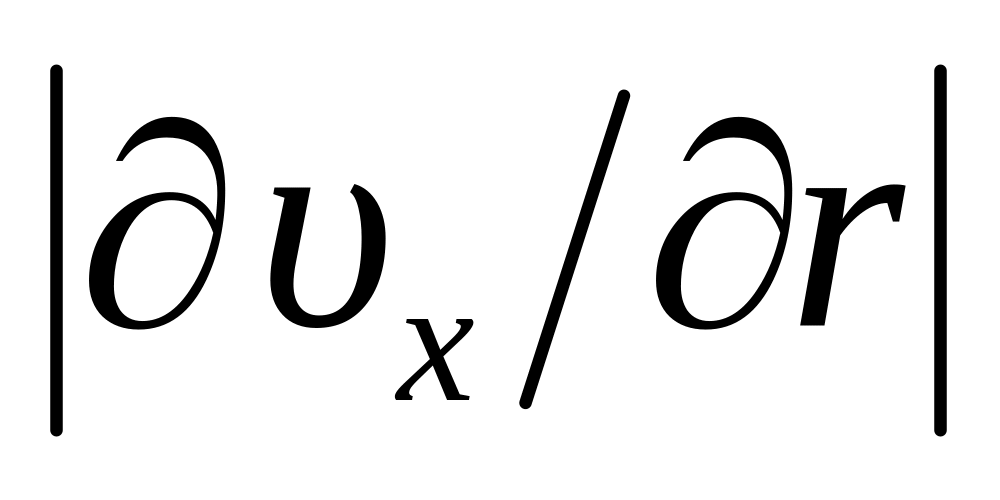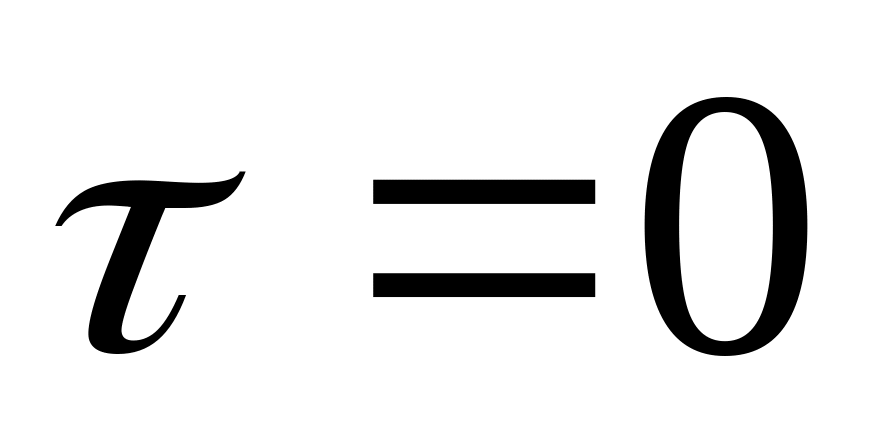2. Функция есть степенная функция своего аргумента. Говоря точней, модуль касательного напряжения является степенной функцией модуля скорости сдвига , причем, так же как и в предыдущем случае, при 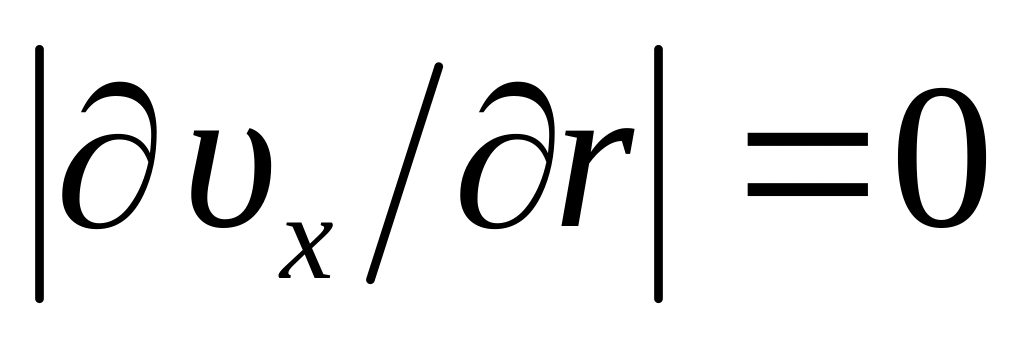. Иными словами, имеет место соотношение

, (7.4)

а само реологическое уравнение (7.1) может быть представлено в виде:

. (7.5)

Такая запись показывает, что модуль касательного напряжения дается формулой (7.4), а его знак совпадает со знаком производной .

Жидкость, удовлетворяющую реологическому соотношению (7.4), называют неньютоновской степенной жидкостью или степенной жидкостью Освальда. Коэффициент , входящий в это уравнение, называют косистентностью жидкости, а показателем степени: если , то жидкость называют псевдопластичной, если же дилатантной. Размерность консистентности равна, очевидно, . При степенная жидкость является ньютоновской вязкой жидкостью, причем коэффициент .

7.1. Распределение касательного напряжения в сечении трубы

Выделим в жидкости, движущейся в трубе, цилиндр радиуса с длиной (рис. 7.1.).

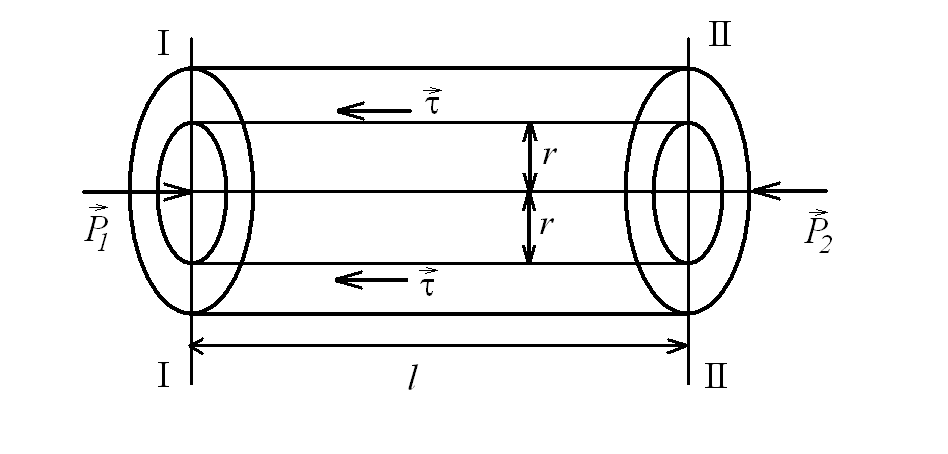
Рис. 7.1. Равновесие сил на поверхности цилиндра

Рассмотрим силы, действующие на выделенный цилиндр. В сечении (1—1) действует сила давления , в сечении (2—2) - сила , где и давления в сечениях (1—1) и (2—2). На боковую поверхность цилиндра действует сила трения . Кроме того, имеется еще массовая сила – сила инерции равняя массе жидкости выделенного объема, умноженной на ускорение его центра тяжести со знаком «минус».

Уравнение равновесия всех этих сил в проекции на ось трубы имеет вид:

. (7.6)

Поскольку движение жидкости считается установившимся, то . Кроме того, из уравнения неразрывности следует, что , следовательно, ускорение . Действительно

.

Тогда из уравнения (7.6) баланса сил заключаем, что распределение модуля касательного напряжения по радиусу трубы будет линейным:

, (7.7)

где . В частности, модуль касательного напряжения на внутренней поверхности трубы выражается формулой

. (7.8)

Используя (7.8), распределению (7.7) можно придать следующий вид:

. (7.9)

Отсюда видно, что касательное напряжение минимально на оси трубы ( ) и максимально на внутренней поверхности трубы .