
- •1. Предмет комбінаторики. Правила суми і добутку. Перестановки без повторення . Перестановки з повтореннями.
- •2.Розміщення без повторення. Розміщення з повтореннями.
- •5. Трикутник Паскаля, біном Ньютона. Число всіх підмножин множини.
- •6.Комбінації з повтореннями.
- •7. Формули включень та виключень; вміти записати для 2 і 3.
- •8.Простір елементарних подій. Операції над подіями. Класичне означення ймовірності. Статистичне означення ймовірності.
- •9.Теорема додавання ймовірностей для несумісних подій. Теорема додавання ймовірностей для сумісних подій.
- •10.Залежні та незалежні події, умовна ймовірність.
- •11.Теорема множення для двох випадкових подій. Теорема множення для довільних випадкових подій.
- •12.Попарно залежні та незалежні у сукупності події. Приклад Бернштейна.
- •13.Геометричні ймовірності. Задача про зустріч. Задача Бюффона.
- •14. Ймовірність появи хоча б однієї випадкової події. Задача про товсту монету.
- •15.Формула повної ймовірності. Формула Бейеса.
- •1.Формула повної ймовірності
- •16. Формула Бернулі. Найймовірніше число “успіхів” у схемі Бернулі.
- •17.Теорема Пуассона
- •18. Локальна теорема Муавра-Лапласа. Функція Гаусса.
- •19. Інтегральна теорема Муавра-Лапласа. Функція Лапласа.
- •20.Поняття випадкової величини. Функція розподілу. Приклади. Властивості функцій розподілу.
- •21.Закон розподілу дискретної випадкової величини. Математичне сподівання двв та його властивості.
- •Дисперсія двв та його властивості. Середнє квадратичне відхилення.
- •Математичне сподівання та дисперсія біномного розподілу двв.
- •24.Диференціальна функція розподілу неперервної випадкової величини, її властивості та ймовірносний смисл.
- •25. Відшукання інтегральної функції неперервної випадкової величини за відомою диференціальною функцією. Доведення рівності та її геометричний зміст.
- •26.Числові характеристики неперервної випадкової величини.
- •27. Нормальний закон розподілу, його параметри та графік. Зв’язок між функцією розподілу нормального закону та функцією Лапласа.
- •28.Ймовірність попадання нормально розподіленої величини в заданий інтервал.
- •29. Правило трьох сигм.
- •30. Поняття про закон великих чисел. Нерівності Чебишева.
- •31.Мода та медіана, квантилі.
- •32.Рівномірний розподіл та його числові характеристики.
- •Показниковий розподіл та його числові характеристики.
- •34. Закон розподілу Пуассона
- •35.Геометричний розподіл та його числові характеристики.
- •36. Початкові та центральні моменти. Асиметрія та ексцес.
- •37.Приклади: асиметрія показникового розподілу; асиметрія розподілу Пуассона.
- •Розподіл Пуассона
- •38.Теорема Чебишова.
- •39.Теорема Бернуллі
- •40. Центральна гранична теорема.
- •Классическая формулировка ц.П.Т.
- •41. Випадковий процес та його характеристики.
- •42.**Ланцюгі Маркова
- •Формальне визначення Послідовність дискретних випадкових величин називається ланцюгом Маркова (з дискретним часом), якщо
- •43.**Марківський випадковий процес. Потоки подій.
- •**Пуассонівський випадковий процес.
- •45. Поняття про генеральну сукупність та вибірку. Емпірична формула розподілу.
- •46. Вибіркові характеристики. Варіаційний ряд, таблиці частот, гістограма.
- •47.Полігон частот. Статистичне та інтервальне оцінювання параметрів розподілу.
- •48. Вибіркове середнє, вибіркова дисперсія. Інтервальні оцінки параметрів розподілу.
- •49.Надійні межі для математичного сподівання у випадку нормального розподілу.
- •50.Статистична гіпотеза та загальна схема її перевірки. Критерій Пірсона.
19. Інтегральна теорема Муавра-Лапласа. Функція Лапласа.
В приложениях схемы Бернулли часто возникает вопрос найти вероятность, что число наступлений события А (m) лежит в заданных пределах.
Такую
вероятность обозначим:
![]() .
.
Указанная вероятность может быть найдена по асимптотической формуле.
Теорема
(интегральная теорема Муавра-Лапласа):
пусть в схеме Бернулли
![]() и
“n” – достаточно велико (“n”>100,
npq>20).
и
“n” – достаточно велико (“n”>100,
npq>20).
Тогда справедлива приближенная формула:
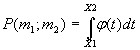 (Формула
5) , где
(Формула
5) , где
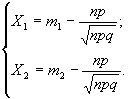
Пользуясь формулой Ньютона – Лейбница, Формулу (5) записывают следующим образом:
![]() (Формула
6).
(Формула
6).
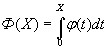 –
функция
Лапласа.
–
функция
Лапласа.
![]()
Значения Ф даны в таблицах.
20.Поняття випадкової величини. Функція розподілу. Приклади. Властивості функцій розподілу.
Випадковою
величиною є будь-яка (не обов'язково
числова) змінна ![]() ,
"значення" якої
,
"значення" якої ![]() утворюють множину
утворюють множину ![]() елементарних
подій,
або, іншими словами, позначають точки
в просторі вибірок.
Відповідний розподіл
імовірностей називається
розподілом випадкової величини
. [2]
елементарних
подій,
або, іншими словами, позначають точки
в просторі вибірок.
Відповідний розподіл
імовірностей називається
розподілом випадкової величини
. [2]
Множина елементарних подій являє собою можливі значення випадкової величини , називається областю значень цієї величини.
Функція розподілу в теорії ймовірностей - функція, що характеризує розподіл випадкової величини або випадкового вектора. При дотриманні певних умов повністю визначає випадкову величину.
Нехай
дано ймовірнісна
простір ![]() ,
І на ньому визначена випадкова
величина X з
розподілом
,
І на ньому визначена випадкова
величина X з
розподілом ![]() .
Тоді функцією розподілу випадкової
величини Xназивається функція
.
Тоді функцією розподілу випадкової
величини Xназивається функція ![]() ,
Що задається формулою:
,
Що задається формулою:
![]() .
.
Тобто
функцією розподілу (ймовірностей)
випадкової величини X називають функцію
F (x), значення якої в точці x одно ймовірності
події ![]() ,
Тобто події, що складається тільки з
тих елементарних результатів, для
яких
,
Тобто події, що складається тільки з
тих елементарних результатів, для
яких ![]() .
.
Властивості
F X неперервна справа: [1]
![]()
F X не убуває на всій числовій прямій.
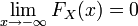 .
.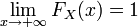 .
.
Розподіл випадкової величини однозначно визначає функцію розподілу.
Вірно і зворотне: якщо функція F (x) задовольняє чотирьом перерахованим вище властивостям, то існує ймовірнісна простір і визначена на ньому випадкова величина, така що F (x) є її функцією розподілу.
За визначенням безперервності справа, функція F X має правий межа F X (x +) в будь-якій точці
 ,
І він співпадає із значенням
функції F X (x) в
цій точці.
,
І він співпадає із значенням
функції F X (x) в
цій точці.В силу неубиванія, функція F X також має і лівий межа F X (x -) в будь-якій точці , Який може не співпадати із значенням функції. Таким чином, функція F X або неперервна в точці, або має в ній розрив першого роду
21.Закон розподілу дискретної випадкової величини. Математичне сподівання двв та його властивості.
Законом розподілу дискретної випадкової величини на-
зивають відповідність між можливими значеннями і їх імовірностями. Його задають таблично, графічно чи аналітич-но (у виді формул).
Дві випадкові величини називаються незалежними, якщо закон розподілу однієї з них не залежить від того, які можливі значення прийняла друга величина. В протилежному випадкувипадкові величини є залежними. Декілька випадкових вели-чин називаються взаємно незалежними, якщо закони розпо-ділу будь-якого числа з них не залежать від того, які можливі значення набула решта величин.
Добутком незалежних випадкових величин Х та Y нази-вають випадкову величину ХY, можливі значення якої рівні всеможливим добуткам співмножників Х і Y. Імовірності цих добутків рівні добуткам імовірностей відповідних співмнож-ників. Якщо деякі добутки ХіГі рівні між собою, то імовірність цього добутку рівна сумі імовірностей цих добутків.
Сумою випадкових величин Х і Y називають випадкову величину Х + Y, можливі значення якої рівні всеможливим су-мам з доданків Х та Y. Імовірності цих сум рівні добуткам імовірностей доданків; для залежних величин - добуткам імо-вірностей одного доданку на умовну імовірність другого, якщо деякі суми рівні між собою, то імовірність такої суми рівна сумі відповідних імовірностей доданків.
Математичним сподіванням дискретної випадкової ве-личини називають суму добутків всіх її можливих значень на їх імовірності:
Властивості математичного сподівання:
Математичне сподівання сталої величини є сама ця стала: М{С) = С.
Сталий множник можна виносити за знак математич-ного сподівання.
Математичне сподівання добутку двох незалежних випадкових величин дорівнює добутку їх математичних сподівань:
