8.Простір елементарних подій. Операції над подіями. Класичне означення ймовірності. Статистичне означення ймовірності.

Простір елементарних подій — множина всіх можливих наслідків стохастичного експерименту. Тобто, множина елементарних подій. Зазвичай позначаєтеся літерою Ω, також S або U.

Простір елементарних подій називається дискретним, якщо множина Ω скінченна або зліченна.

Приклад

Припустимо, що монету підкидають один раз. Простір елементарних подій, цього експерименту має вигляд Ω = {Г, Р}, де Г означає появу герба, буква Р — появу решки. Монету підкидають двічі. Простором елементарних подій цього експерименту є множина Ω = {ГГ, ГР, РГ, РР}. Тут ГР означає, наприклад, що при першому підкиданні з'явився герб, а при другому — решка.

Підкидають шестигранний гральний кубик на якому вибиті очки від 1 до 6. Нас цікавить число очок, яке випало. Простором елементарних подій тут може бути Ω = {1,2,3,4,5,6}.

Операції над подіями.

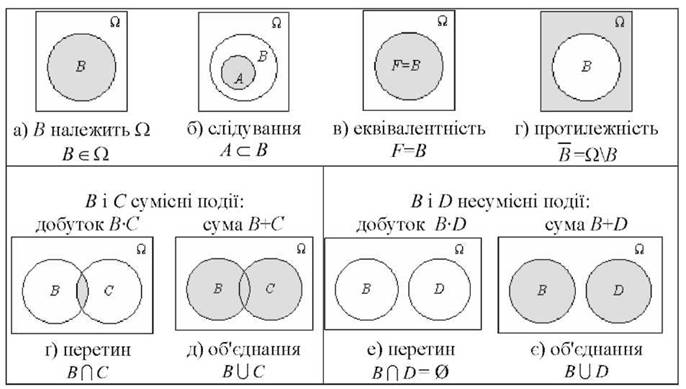
Класичне означення ймовірності: Імовірністю випадкової події А називається відношення кількості елементарних подій m, які сприяють появі цієї події (становлять множину її елементарних подій), до загальної кількості n рівноможливих елементарних подій, що утворюють простір елементарних подій W:

P(A)=m/n;

Щоб обчислити ймовірність події А за цією формулою, потрібно знайти кількість елементарних подій у просторі W, а також кількість їх у множині, яка відповідає події А. Для цього застосовують формули комбінаторики.

Статистичне означення ймовірності: Статистичною ймовірністю події А називається відношення кількості m випробувань, в яких подія А відбулась, до загальної кількості виконаних випробувань n: W(A)=m/n;

9.Теорема додавання ймовірностей для несумісних подій. Теорема додавання ймовірностей для сумісних подій.

Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из орудия произведены два выстрела и А — попадание при первом выстреле, В — попадание при втором выстреле, то А + В — попадание при первом выстреле, или при втором, или в обоих выстрелах

Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.

Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р (А + В) = Р (А) + Р (В).

С л е д с т в и е. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий: Р (A₁ + A₂ + ... + A_n) = Р (A₁) + Р (A₂) + ... + Р (A_n).

Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

Р (А + В) = Р (А) + Р (В) - Р (АВ).

Теорема может быть обобщена на любое конечное число совместных событий. Например, для трех совместных событий Р(А + В+С) = Р(А) + Р(В) + + Р(С) - Р(АВ) - Р(АС) - Р(ВС) + Р(АВС).