
- •1. Предмет комбінаторики. Правила суми і добутку. Перестановки без повторення . Перестановки з повтореннями.
- •2.Розміщення без повторення. Розміщення з повтореннями.
- •5. Трикутник Паскаля, біном Ньютона. Число всіх підмножин множини.
- •6.Комбінації з повтореннями.
- •7. Формули включень та виключень; вміти записати для 2 і 3.
- •8.Простір елементарних подій. Операції над подіями. Класичне означення ймовірності. Статистичне означення ймовірності.
- •9.Теорема додавання ймовірностей для несумісних подій. Теорема додавання ймовірностей для сумісних подій.
- •10.Залежні та незалежні події, умовна ймовірність.
- •11.Теорема множення для двох випадкових подій. Теорема множення для довільних випадкових подій.
- •12.Попарно залежні та незалежні у сукупності події. Приклад Бернштейна.
- •13.Геометричні ймовірності. Задача про зустріч. Задача Бюффона.
- •14. Ймовірність появи хоча б однієї випадкової події. Задача про товсту монету.
- •15.Формула повної ймовірності. Формула Бейеса.
- •1.Формула повної ймовірності
- •16. Формула Бернулі. Найймовірніше число “успіхів” у схемі Бернулі.
- •17.Теорема Пуассона
- •18. Локальна теорема Муавра-Лапласа. Функція Гаусса.
- •19. Інтегральна теорема Муавра-Лапласа. Функція Лапласа.
- •20.Поняття випадкової величини. Функція розподілу. Приклади. Властивості функцій розподілу.
- •21.Закон розподілу дискретної випадкової величини. Математичне сподівання двв та його властивості.
- •Дисперсія двв та його властивості. Середнє квадратичне відхилення.
- •Математичне сподівання та дисперсія біномного розподілу двв.
- •24.Диференціальна функція розподілу неперервної випадкової величини, її властивості та ймовірносний смисл.
- •25. Відшукання інтегральної функції неперервної випадкової величини за відомою диференціальною функцією. Доведення рівності та її геометричний зміст.
- •26.Числові характеристики неперервної випадкової величини.
- •27. Нормальний закон розподілу, його параметри та графік. Зв’язок між функцією розподілу нормального закону та функцією Лапласа.
- •28.Ймовірність попадання нормально розподіленої величини в заданий інтервал.
- •29. Правило трьох сигм.
- •30. Поняття про закон великих чисел. Нерівності Чебишева.
- •31.Мода та медіана, квантилі.
- •32.Рівномірний розподіл та його числові характеристики.
- •Показниковий розподіл та його числові характеристики.
- •34. Закон розподілу Пуассона
- •35.Геометричний розподіл та його числові характеристики.
- •36. Початкові та центральні моменти. Асиметрія та ексцес.
- •37.Приклади: асиметрія показникового розподілу; асиметрія розподілу Пуассона.
- •Розподіл Пуассона
- •38.Теорема Чебишова.
- •39.Теорема Бернуллі
- •40. Центральна гранична теорема.
- •Классическая формулировка ц.П.Т.
- •41. Випадковий процес та його характеристики.
- •42.**Ланцюгі Маркова
- •Формальне визначення Послідовність дискретних випадкових величин називається ланцюгом Маркова (з дискретним часом), якщо
- •43.**Марківський випадковий процес. Потоки подій.
- •**Пуассонівський випадковий процес.
- •45. Поняття про генеральну сукупність та вибірку. Емпірична формула розподілу.
- •46. Вибіркові характеристики. Варіаційний ряд, таблиці частот, гістограма.
- •47.Полігон частот. Статистичне та інтервальне оцінювання параметрів розподілу.
- •48. Вибіркове середнє, вибіркова дисперсія. Інтервальні оцінки параметрів розподілу.
- •49.Надійні межі для математичного сподівання у випадку нормального розподілу.
- •50.Статистична гіпотеза та загальна схема її перевірки. Критерій Пірсона.
45. Поняття про генеральну сукупність та вибірку. Емпірична формула розподілу.
Основна мета використання методів математичної статистики - вивчення властивостей незмірно великої групи об'єктів на підставі аналізу властивостей відносно невеликий їх сукупності.
При цьому все існуюче в природі, цікавлячі нас об'єкти називаються генеральною сукупністю, а відносно невелика їх кількість, відібрана нами для вивчення - вибіркової сукупністю, або вибіркою.
Емпіричною функцією розподілу Fn(x) називається відносна частота (частість) того, що ознака (випадкова величина Х) прийме значення, менше ніж заданий х, тобто
Fn(x)=w(X<x)=
![]()
Іншими
словами емпірична функція розподілу
являє собою нагромаджену частість
=
![]()
Можна помітити, що статистичний ряд – це статистичний аналог розподілу ознаки (випадкової величини Х).
46. Вибіркові характеристики. Варіаційний ряд, таблиці частот, гістограма.
Варіаційним рядом х(1) х(2) ... х(n) називається вибірка, записана в порядку зростання її елементів. Числові характеристики емпіричного розподілу називаються вибірковими характеристиками: вибіркові середнє (математичне сподівання), дисперсія:

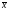 =
= , s2=
, s2=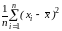
вибірковий момент порядку k:
mk
=
 ;
;
вибіркові квантилі p порядку р - корені рівняння
F(p)=p,
якими є члени варіаційного ряду
(p)=([np]+1), де [nр] означає ціла частина nр; частинним випадком (p = 0.5) є вибіркова медіана - центральний член варіаційного ряду. Значення вибіркових характеристик полягає в тому, що при n вони прямують до значень розподілу F(х). У випадку дискретної емпіричної випадкової величини статистичний розподіл подають у вигляді таблиці розподілу частот:

 Гістограми
використовують для зображення винятково
інтервальних варіаційних рядів. Для її
побудови в прямокутній системі координат
на осі абсцис відкладають відрізки, що
є частковими інтервалами спостережень.
На цих відрізках, як на основах, будують
прямокутники з висотами, що дорівнюють
частотам — абсолютним або відносним.
Гістограмою
абсолютних частот
називають ступінчасту фігуру, яка
побудована з прямокутників, основою
яких є інтервали групування, довжини
h,
а висоти дорівнюють
Гістограми
використовують для зображення винятково
інтервальних варіаційних рядів. Для її
побудови в прямокутній системі координат
на осі абсцис відкладають відрізки, що
є частковими інтервалами спостережень.
На цих відрізках, як на основах, будують
прямокутники з висотами, що дорівнюють
частотам — абсолютним або відносним.
Гістограмою
абсолютних частот
називають ступінчасту фігуру, яка
побудована з прямокутників, основою
яких є інтервали групування, довжини
h,
а висоти дорівнюють
 .
Площа
гістограми абсолютних частот дорівнює
п.
.
Площа
гістограми абсолютних частот дорівнює
п.
47.Полігон частот. Статистичне та інтервальне оцінювання параметрів розподілу.
Статистичні оцінки діляться на точкові та інтервальні. Точковою називається оцінка, яка визначається одним числом.. При вибірці малого обсягу точкові оцінки можуть значно відхилятись від параметру, тобто приводять до грубих похибок. Тому більш точними є інтервальні оцінки.
Інтервальною називають оцінку, яка визначається двома числами – кінцями інтервалу. Інтервальні оцінки дозволяють встановити точність і надійність оцінок.
Нехай
знайдена по даних вибірки статистична
характеристика а* служить
оцінкою невідомого параметру а.
Будемо вважати а постійною
величиною (може бути і випадковою).
Зрозуміло, що а* тим
точніше визначає параметр а,
чим менша абсолютна величина різниці ![]() .
Іншими словами, якщо
.
Іншими словами, якщо ![]() і
і ![]() ,
то чим менше
,
то чим менше ![]() ,
тим точніша оцінка. Таким чином, додатне
число
характеризує точність
оцінки.
,
тим точніша оцінка. Таким чином, додатне
число
характеризує точність
оцінки.
В
зв’язку з тим, що вибіркові параметри
(середні, дисперсія і т.д.) є випадковими
величинами, то і їх відхилення від
генеральних параметрів (похибки) також
будуть випадковими величинами. Таким
чином, задачу про оцінку цих відхилень
носить ймовірнісний характер і полягає
в оцінці ймовірності ![]() ,
наприклад:
,
наприклад:
![]() чи
чи ![]() і
т.д. Ймовірність
і
т.д. Ймовірність ![]() (як
правило
(як
правило ![]() ) називається
надійністю,
а інтервали
) називається
надійністю,
а інтервали ![]() і
т.д. називаються
надійними інтервалами, або довірчими
інтервалами.
В загальному випадку надійністю
оцінкиа по а* називається
ймовірність
і
т.д. називаються
надійними інтервалами, або довірчими
інтервалами.
В загальному випадку надійністю
оцінкиа по а* називається
ймовірність ![]() ,
з якою здійснюється нерівність
,
а інтервал
,
з якою здійснюється нерівність
,
а інтервал ![]() ,
який з заданою надійністю
накриває
невідомий параметр а і
називається довірчим інтервалом.
,
який з заданою надійністю
накриває
невідомий параметр а і
називається довірчим інтервалом.
Полігон частот - ламана, що з'єднує точки. Полігон частот образується ламаною лінією, яка з’єднує точки, відповідним середнім значенням інтервалів групування та частотами цих інтервалів, середнє значення відкладається на осі х, а частоти на осі У.Полігоном частот називається залежність варіант ряду розподілу від частоти або відносної частоти.
