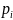- •1. Предмет комбінаторики. Правила суми і добутку. Перестановки без повторення . Перестановки з повтореннями.
- •2.Розміщення без повторення. Розміщення з повтореннями.
- •5. Трикутник Паскаля, біном Ньютона. Число всіх підмножин множини.
- •6.Комбінації з повтореннями.
- •7. Формули включень та виключень; вміти записати для 2 і 3.
- •8.Простір елементарних подій. Операції над подіями. Класичне означення ймовірності. Статистичне означення ймовірності.
- •9.Теорема додавання ймовірностей для несумісних подій. Теорема додавання ймовірностей для сумісних подій.
- •10.Залежні та незалежні події, умовна ймовірність.
- •11.Теорема множення для двох випадкових подій. Теорема множення для довільних випадкових подій.
- •12.Попарно залежні та незалежні у сукупності події. Приклад Бернштейна.
- •13.Геометричні ймовірності. Задача про зустріч. Задача Бюффона.
- •14. Ймовірність появи хоча б однієї випадкової події. Задача про товсту монету.
- •15.Формула повної ймовірності. Формула Бейеса.
- •1.Формула повної ймовірності
- •16. Формула Бернулі. Найймовірніше число “успіхів” у схемі Бернулі.
- •17.Теорема Пуассона
- •18. Локальна теорема Муавра-Лапласа. Функція Гаусса.
- •19. Інтегральна теорема Муавра-Лапласа. Функція Лапласа.
- •20.Поняття випадкової величини. Функція розподілу. Приклади. Властивості функцій розподілу.
- •21.Закон розподілу дискретної випадкової величини. Математичне сподівання двв та його властивості.
- •Дисперсія двв та його властивості. Середнє квадратичне відхилення.
- •Математичне сподівання та дисперсія біномного розподілу двв.
- •24.Диференціальна функція розподілу неперервної випадкової величини, її властивості та ймовірносний смисл.
- •25. Відшукання інтегральної функції неперервної випадкової величини за відомою диференціальною функцією. Доведення рівності та її геометричний зміст.
- •26.Числові характеристики неперервної випадкової величини.
- •27. Нормальний закон розподілу, його параметри та графік. Зв’язок між функцією розподілу нормального закону та функцією Лапласа.
- •28.Ймовірність попадання нормально розподіленої величини в заданий інтервал.
- •29. Правило трьох сигм.
- •30. Поняття про закон великих чисел. Нерівності Чебишева.
- •31.Мода та медіана, квантилі.
- •32.Рівномірний розподіл та його числові характеристики.
- •Показниковий розподіл та його числові характеристики.
- •34. Закон розподілу Пуассона
- •35.Геометричний розподіл та його числові характеристики.
- •36. Початкові та центральні моменти. Асиметрія та ексцес.
- •37.Приклади: асиметрія показникового розподілу; асиметрія розподілу Пуассона.
- •Розподіл Пуассона
- •38.Теорема Чебишова.
- •39.Теорема Бернуллі
- •40. Центральна гранична теорема.
- •Классическая формулировка ц.П.Т.
- •41. Випадковий процес та його характеристики.
- •42.**Ланцюгі Маркова
- •Формальне визначення Послідовність дискретних випадкових величин називається ланцюгом Маркова (з дискретним часом), якщо
- •43.**Марківський випадковий процес. Потоки подій.
- •**Пуассонівський випадковий процес.
- •45. Поняття про генеральну сукупність та вибірку. Емпірична формула розподілу.
- •46. Вибіркові характеристики. Варіаційний ряд, таблиці частот, гістограма.
- •47.Полігон частот. Статистичне та інтервальне оцінювання параметрів розподілу.
- •48. Вибіркове середнє, вибіркова дисперсія. Інтервальні оцінки параметрів розподілу.
- •49.Надійні межі для математичного сподівання у випадку нормального розподілу.
- •50.Статистична гіпотеза та загальна схема її перевірки. Критерій Пірсона.
34. Закон розподілу Пуассона
Дискретна
випадкова величина має розподіл Пуассона,
якщо вона набуває зліченної множини
значень ![]() з імовірностями
з імовірностями ![]() Цей
розподіл описує кількість подій, які
настають в однакові проміжки часу за
умови, що ці події відбуваються незалежно
одна від одної зі сталою інтенсивністю.
Розподіл застосовується в задачах
статистичного контролю якості, у теорії
надійності, теорії масового обслуговування.
Математичне сподівання і дисперсія в
цьому розподілі однакові і дорівнюють
а.
Для цього розподілу складено таблиці
щодо різних значень
Цей
розподіл описує кількість подій, які
настають в однакові проміжки часу за
умови, що ці події відбуваються незалежно
одна від одної зі сталою інтенсивністю.
Розподіл застосовується в задачах
статистичного контролю якості, у теорії
надійності, теорії масового обслуговування.
Математичне сподівання і дисперсія в
цьому розподілі однакові і дорівнюють
а.
Для цього розподілу складено таблиці
щодо різних значень ![]() (0,1—20).
У таблицях для відповідних значень а наведено
ймовірності
(0,1—20).
У таблицях для відповідних значень а наведено
ймовірності ![]()
Якщо у схемі незалежних повторних випробувань n велике і р або 1 – р прямують до нуля, то біноміальний розподіл апроксимується розподілом Пуассона, коли λ=n*p
Числові характеристики положення про розподіл Пуассона
Математичним очікуванням дискретної випадкової величини називають суму творів всіх її можливих значень на їх імовірності.
M(X)=λ
Модою випадкової величини називається її найбільш ймовірне значення.
Числові характеристики розкиду
Дисперсією випадкової величини Х називають математичної очікування квадрата відхилення випадкової величини від її математичного сподівання.
Середнім квадратичним відхиленням (стандартним відхиленням або стандартом) випадкової величини Х називається арифметичне значення кореня квадратного з її дисперсії. D(X)=λ
35.Геометричний розподіл та його числові характеристики.
Нехай
проводиться n незалежних експериментів,
у кожному з яких з однаковою ймовірністю
р може відбутися деяка подія А. Випробування
закінчуються, як тільки подія А
відбулася. Тобто, якщо А з’явилася у
k-му випробуванні, то в перших (k-1)
випробуваннях подія А не відбулася.
Випадкова величина Х – номери першого
успішного випробування в схемі Бернуллі
набуває значень 1, 2, 3, …, k, … з
ймовірностями P{X=k}= .
Тоді
випадкова величина Х має геометричний
розподілу з параметром р(що можна
записати у вигляді X
∈Gp
) і
рядом
розподілу
(табл.
5.3):
.
Тоді
випадкова величина Х має геометричний
розподілу з параметром р(що можна
записати у вигляді X
∈Gp
) і
рядом
розподілу
(табл.
5.3):
Таблиця 5.3 - Геометричний ряд розподілу
|
1 |
2 |
3 |
… |
k |
… |
|
p |
(1-p)*p |
|
… |
|
… |
Сума
ймовірностей у другому рядку ряду
розподілу дорівнює одиниці.
Знайдемо
числові характеристики випадкової
величини: математичне
сподівання M(X)=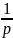 . Дисперсія
D(X)=
. Дисперсія
D(X)=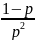 . Середнє
квадратичне відхилення : σ(X)=
. Середнє
квадратичне відхилення : σ(X)=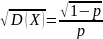
36. Початкові та центральні моменти. Асиметрія та ексцес.
Для дискретної випадкової величини k–й початковий момент визначається за формулою

Для неперервної випадкової величини k–й початковий момент визначається за формулою

Визначення
4.11. Відхилення випадкової величини від
математичного сподівання
![]() називають
центрованою випадковою величиною.
Визначення 4.12. Центральним моментомs-го
порядку µs називають математичне
сподівання s-го степеня центрованої
випадкової величини
називають
центрованою випадковою величиною.
Визначення 4.12. Центральним моментомs-го
порядку µs називають математичне
сподівання s-го степеня центрованої
випадкової величини
![]()
Для дискретної випадкової величини s–й центральний момент визначається за формулою
![]()
Для неперервної випадкової величини s–й центральний момент визначається за формулою
![]()
Оцінку відхилення емпіричного розподілу від нормального проводять за допомогою таких статистичних характеристик, як коефіцієнти асиметрії, тобто ступеня скошеності варіаційного ряду розподілу відносно його симетрії вправо або вліво, і гостровершинності – ексцесу. При зміщенні вправо від центру асиметрія матиме додатне число, при зміщенні вліво – від’ємне.
Коефіцієнт асиметрії (As) обчислюється як відношення центрального моменту третього порядку до куба середнього квадратичного відхилення

Характер скошеності функції щільності розподілу Р(х) визначається значенням асиметрії As
. При A=0 крива ймовірності р(х) симетрична,
при А>0 витягнута її права частина, а
при А<0 – ліва частина спаду. Коефіцієнт
асиметрії є нормованим моментом третього
порядку (µ3)
Коефіцієнт ексцесу (англ. Kurtosis) —
числова характеристика розподілу
ймовірностей дійсної випадкової
величини.
Коефіцієнт ексцесу характеризує
«крутість», тобто, стрімкість підвищення
кривої розподілу у порівнянні з нормальною
кривою.
Ексцесом
При A=0 крива ймовірності р(х) симетрична,
при А>0 витягнута її права частина, а
при А<0 – ліва частина спаду. Коефіцієнт
асиметрії є нормованим моментом третього
порядку (µ3)
Коефіцієнт ексцесу (англ. Kurtosis) —
числова характеристика розподілу
ймовірностей дійсної випадкової
величини.
Коефіцієнт ексцесу характеризує
«крутість», тобто, стрімкість підвищення
кривої розподілу у порівнянні з нормальною
кривою.
Ексцесом ![]() (за
Фішером) теоретичного розподілу називають
характеристику, що обчислюється за
наступною формулою:
(за
Фішером) теоретичного розподілу називають
характеристику, що обчислюється за
наступною формулою:
![]() ,
,
де ![]() — центральний
момент четвертого порядку,
— дисперсія.
— центральний
момент четвертого порядку,
— дисперсія.