
- •1. Предмет комбінаторики. Правила суми і добутку. Перестановки без повторення . Перестановки з повтореннями.
- •2.Розміщення без повторення. Розміщення з повтореннями.
- •5. Трикутник Паскаля, біном Ньютона. Число всіх підмножин множини.
- •6.Комбінації з повтореннями.
- •7. Формули включень та виключень; вміти записати для 2 і 3.
- •8.Простір елементарних подій. Операції над подіями. Класичне означення ймовірності. Статистичне означення ймовірності.
- •9.Теорема додавання ймовірностей для несумісних подій. Теорема додавання ймовірностей для сумісних подій.
- •10.Залежні та незалежні події, умовна ймовірність.
- •11.Теорема множення для двох випадкових подій. Теорема множення для довільних випадкових подій.
- •12.Попарно залежні та незалежні у сукупності події. Приклад Бернштейна.
- •13.Геометричні ймовірності. Задача про зустріч. Задача Бюффона.
- •14. Ймовірність появи хоча б однієї випадкової події. Задача про товсту монету.
- •15.Формула повної ймовірності. Формула Бейеса.
- •1.Формула повної ймовірності
- •16. Формула Бернулі. Найймовірніше число “успіхів” у схемі Бернулі.
- •17.Теорема Пуассона
- •18. Локальна теорема Муавра-Лапласа. Функція Гаусса.
- •19. Інтегральна теорема Муавра-Лапласа. Функція Лапласа.
- •20.Поняття випадкової величини. Функція розподілу. Приклади. Властивості функцій розподілу.
- •21.Закон розподілу дискретної випадкової величини. Математичне сподівання двв та його властивості.
- •Дисперсія двв та його властивості. Середнє квадратичне відхилення.
- •Математичне сподівання та дисперсія біномного розподілу двв.
- •24.Диференціальна функція розподілу неперервної випадкової величини, її властивості та ймовірносний смисл.
- •25. Відшукання інтегральної функції неперервної випадкової величини за відомою диференціальною функцією. Доведення рівності та її геометричний зміст.
- •26.Числові характеристики неперервної випадкової величини.
- •27. Нормальний закон розподілу, його параметри та графік. Зв’язок між функцією розподілу нормального закону та функцією Лапласа.
- •28.Ймовірність попадання нормально розподіленої величини в заданий інтервал.
- •29. Правило трьох сигм.
- •30. Поняття про закон великих чисел. Нерівності Чебишева.
- •31.Мода та медіана, квантилі.
- •32.Рівномірний розподіл та його числові характеристики.
- •Показниковий розподіл та його числові характеристики.
- •34. Закон розподілу Пуассона
- •35.Геометричний розподіл та його числові характеристики.
- •36. Початкові та центральні моменти. Асиметрія та ексцес.
- •37.Приклади: асиметрія показникового розподілу; асиметрія розподілу Пуассона.
- •Розподіл Пуассона
- •38.Теорема Чебишова.
- •39.Теорема Бернуллі
- •40. Центральна гранична теорема.
- •Классическая формулировка ц.П.Т.
- •41. Випадковий процес та його характеристики.
- •42.**Ланцюгі Маркова
- •Формальне визначення Послідовність дискретних випадкових величин називається ланцюгом Маркова (з дискретним часом), якщо
- •43.**Марківський випадковий процес. Потоки подій.
- •**Пуассонівський випадковий процес.
- •45. Поняття про генеральну сукупність та вибірку. Емпірична формула розподілу.
- •46. Вибіркові характеристики. Варіаційний ряд, таблиці частот, гістограма.
- •47.Полігон частот. Статистичне та інтервальне оцінювання параметрів розподілу.
- •48. Вибіркове середнє, вибіркова дисперсія. Інтервальні оцінки параметрів розподілу.
- •49.Надійні межі для математичного сподівання у випадку нормального розподілу.
- •50.Статистична гіпотеза та загальна схема її перевірки. Критерій Пірсона.
1. Предмет комбінаторики. Правила суми і добутку. Перестановки без повторення . Перестановки з повтореннями.
Комбінаторика – розділ математики, предметом якого є теоріяскінченних множин
Сполучення з повтореннямиПоєднанням з повтореннями називаються набори, в яких кожен елемент може брати участь кілька разів.
Перестановки без повторень
- комбінаторні сполуки, які можуть відрізнятися
один від
одного лише порядком елементів
,що входять
до них.
![]()
Послідовність довжини n, складена з k різних символів, перший з яких повторюється n1 раз, другий - n2 раз, третій - n3 раз, ..., k-й - nk раз (де n1 + n2 + ... + nk = n) називається перестановкою з повтореннями з n елементів.
В основі комбінаторики лежать два елементарні правила – суми і добутку.
Сформулюємо правило суми.
( ) , ( ) , N A m N B n A B = = ∩ = Ø ⇒ ∪ = + N A B m n ( ) .
Правило добутку (основне правило комбінаторики): якщо I-у дію можна здійснити n1 способами, II-у, яка не залежить від першої, – n2 способами, ..., k- ту, яка не залежить від усіх попередніх, – nk способами, то першу, другу, ..., k-ту дії послідовно можна здійснити n1n2...nk способами.
2.Розміщення без повторення. Розміщення з повтореннями.
Розміщення
з повтореннями
по m
елементів n-елементної
множини A
– це послідовність елементів множини
A,
що має довжину m.Приклад.
При A={a,
b,
c}
розміщення з повтореннями по два елементи
– це пари (a,a),
(a,b),
(a,c),
(b,a),
(b,b),
(b,c),
(c,a),
(c,b),
(c,c).

Розміщення
по m
елементів n-елементної
множини A,
де m£n
– це послідовність елементів множини
A,
що має довжину m
і попарно різні члени. Приклад. При A={a,
b,
c}
розміщення по два елементи – це пари
(a,b),
(a,c),
(b,a),
(b,c),
(c,a),
(c,b).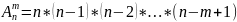
3.
Комбінації без повторення. Рівність
С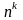 =С
=С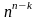 ,
її комбінаторний зміст.
,
її комбінаторний зміст.
Про
комбінації говорять у тих випадках,
коли порядок появи елементів під час
витягування з базової сукупності не є
істотним. Число комбінації без повторень
з n
елементів
по m
елементів позначається символом
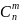 .
Кількість можливих комбінації витягуваних
елементів буде дорівнювати кількості
розрізнюваних перестановок сукупності,
в якій є рівно дві групи нерозрізнюваних
елементів:
.
Кількість можливих комбінації витягуваних
елементів буде дорівнювати кількості
розрізнюваних перестановок сукупності,
в якій є рівно дві групи нерозрізнюваних
елементів:
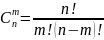 або
або
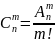 .
Комбінація
без повторень матиме сенс лише тоді,
коли m≤n.
При чому за точної рівності m=n
існує лише одна комбінація, яка дорівнює
базовій. Числа
мають такі очевидні властивості:
.
Комбінація
без повторень матиме сенс лише тоді,
коли m≤n.
При чому за точної рівності m=n
існує лише одна комбінація, яка дорівнює
базовій. Числа
мають такі очевидні властивості:
1.
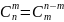
2.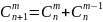
Якщо є деяка комбінаторна конфігурація без повторень, побудована без урахування порядку, то число елементів у такій же комбінатрній конфігурації, але з урахуванням порядку, буде у М разів більше, де М – число можливих різних перестановок об'єктів, що складають елемент.
4.РівністьС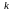
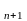 =С
=С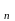
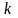 +С
+С
 ,
її комбінаторний зміст
,
її комбінаторний зміст
.
. ![]() .
Ми можемо вибирати підмножини з
.
Ми можемо вибирати підмножини з
![]() елементів наступним чином:
фіксуємо один
елемент; число
-елементних підмножин,
що містять цей елемент,
дорівнює
елементів наступним чином:
фіксуємо один
елемент; число
-елементних підмножин,
що містять цей елемент,
дорівнює
![]() ; число
-елементних підмножин,
що не містять
цей елемент,
дорівнює
; число
-елементних підмножин,
що не містять
цей елемент,
дорівнює
![]() .
.
Доведення теореми (за допомогою комбінаторних міркувань):
Нехай множина A складається з n елементів, це число всіх -елементних підмножин множини А.
Всі k- елементні підмножини множини A розбиваються на 2 групи:
1) підмножини, в які входить a
2)підмножини, в які не входить a
Число підмножин у першій групі: (для того, щоб скласти підмножину першої групи, потрібно до елемента {a} вибрати ( k-1) елемент з (n-1) – елементної множини A \ {a})
Число підмножин у другій групі (для того, щоб скласти підмножину другої групи, потрібно вибрати k елементів з (n-1) - елементної множини A \ {a} )
Значить,
