4.3.3. Связанные колебательные контуры

С овокупность двух или более колебательных контуров, между которыми существует электрическая и магнитная связь, а энергия из одного контура может передаваться в другой, называется связанными колебательными контурами. Рассмотрим в качестве примера двухконтурную схему с трансформаторной связью (рис. 4.31).

Количественно степень связи между контурами оценивается с помощью коэффициента связи , .

Составим и преобразуем уравнения для рассматриваемой схемы:

г де Z₁₁, Z₂₂ – собственные комплексные сопротивления первого и второго контуров, Z ₁₂=Z₂₁=Z_св– общее комплексное сопротивление первого и второго контуров, сопротивление связи.

.

Исследуем подробнее входное сопротивление

,

где Z_1вн – комплексное сопротивление, вносимое из второго контура в первый,

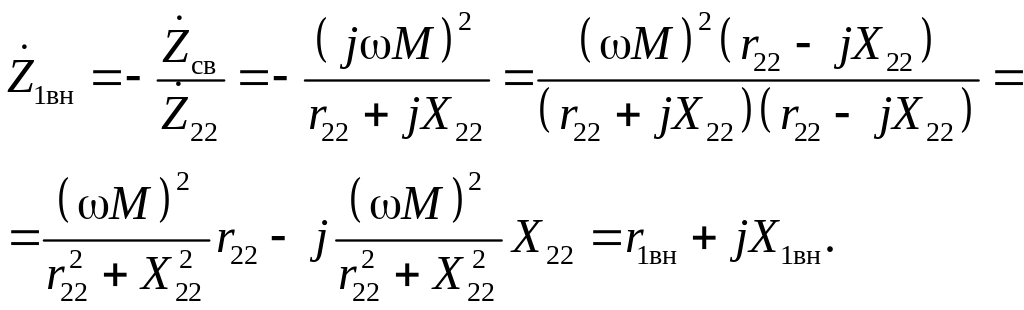
Таким образом, активные и реактивные сопротивления определяются выражениями:

.

Из системы уравнений найдем ток второго контура с учетом того, что ,

.

Это выражение можно записать в виде

,

где – ЭДС, вносимая во второй контур, Z_2вн – вносимое сопротивление:

,

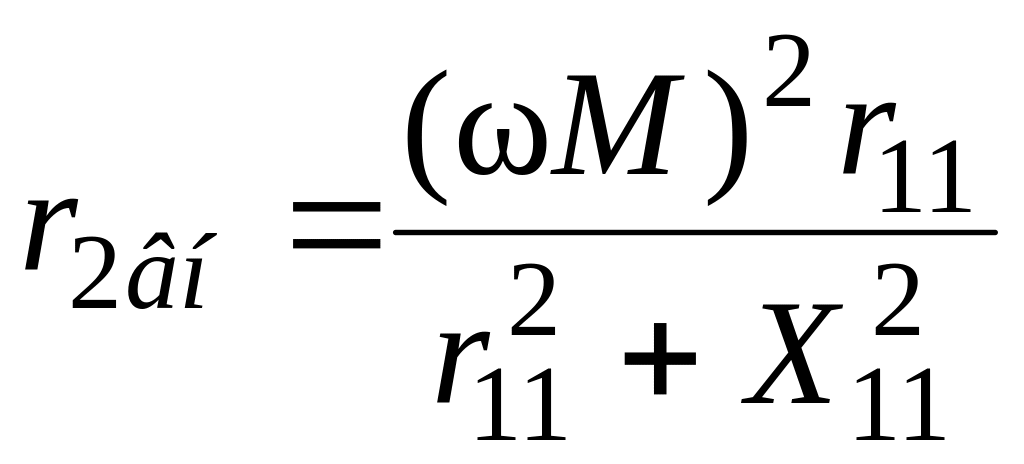Схемы замещения первого и второго контура приведены на рис. 4.32.

И з приведенных выражений видно, что активные составляющие вносимых сопротивлений всегда положительны, а знаки реактивных составляющих вносимых сопротивлений противоположны знакам реактивных составляющих собственных сопротивлений вторичного и первичного контуров X₁₁ и X₂₂. Если, например, на какой-то частоте внешнего воздействия Z₁₁ имеет резистивно-емкостной характер, вносимое во вторичный контур Z_2вн будет иметь резистивно-индуктивный характер.

Резонанс в связанных колебательных контурах

При настройке связанных колебательных контуров добиваются наибольшего значения тока I₂ во вторичном контуре.

Настройку контуров можно вести как за счет изменения параметров реактивных элементов входящих в один или в разные контуры, так и за счет совместного изменения параметров реактивных элементов контуров и параметров элементов связи.

Есть несколько способов настройки связанных контуров.

1. Настройка на первый частный резонанс осуществляется путем изменения параметров реактивных элементов, входящих только в первый контур (Z₂₂, Z₁₂ не изменяются), добиваясь равенства нулю суммы реактивной составляющей собственного сопротивления первичного контура и реактивной составляющей сопротивления, вносимого в первый контур:

X₁₁+ X_1вн=0

Этот способ соответствует настройке на резонансную частоту контура, эквивалентного первичному. Входное сопротивление такого контура относительно зажимов, к которому подключен источник энергии, имеет чисто резистивный характер и ток первичного контура максимален I_1max. Ток второго контура при этом также максимален, поскольку он прямо пропорционален I_1max:

2. Настройку на второй частный резонанс осуществляют путем изменения параметров реактивных элементов, входящих только во второй контур (Z₁₁, Z₁₂ не изменяются), добиваясь равенства нулю суммы реактивной составляющей собственного сопротивления второго контура и реактивной составляющей сопротивления, вносимого во второй контур:

X₂₂+ X_2вн=0

Ток второго контура при этом также достигает другого максимального значения .

3. Настройка на индивидуальный резонанс осуществляется путем изменения параметров реактивных элементов, входящих в оба контура так, чтобы обеспечить равенство нулю мнимой составляющей каждого из контуров при разомкнутом другом контуре:

X₁₁ = X₂₂ = 0

При этом обеспечивается равенство нулю мнимых составляющих сопротивлений, вносимых в каждый из контуров: X_1вн = X_2вн = 0. Таким образом, при настройке на индивидуальный резонанс одновременно выполняются условия настройки на первый и второй частные резонансы.

Когда оба контура настроены , то , Z₂₂=r₂₂ и тогда модуль тока во втором контуре

.

Рассмотренные способы позволяют получить максимальное значение тока вторичного контура при некотором заданном значении сопротивления связи, однако не позволяют достигнуть наибольшего возможного (максимум максиморум) значения тока I₂.

4. Наибольший практический интерес представляет настройка на полный резонанс, которая проводится в два этапа: на первом этапе связанные контуры настраиваются на индивидуальный резонанс, а затем выбирают оптимальное сопротивление связи между ними.

Наибольшее возможное значение будет иметь место при некотором значении сопротивления связи, которое называется оптимальным.

Приравняв нулю производную

,

н айдем оптимальное сопротивление связи , тогда .

Когда оба контура настроены по отдельности, а затем достигнута оптимальная связь, говорят, что связанные контуры настроены в полный резонанс.

Е сли после настройки системы в полный резонанс усилить связь, то возрастут вносимые сопротивления. Теперь уже сопротивление , и во втором контуре не выделится наибольшая мощность. Однако можно вновь достичь выделения наибольшей мощности, если несколько расстроить вторичный контур. В этом случае возрастает реактивное сопротивление , что уменьшает вносимое активное сопротивление , и вновь можно добиться равенства , но уже при некоторых частотах, больших или меньших резонансной. Эти частоты называют частотами связи ( и ) (рис. 4.33).

При полном резонансе оптимальный коэффициент связи

,

где d₁ и d₂ – затухания контуров. Если связанные контуры имеют одинаковые параметры, то d₁ = d₂ и .

При одинаковых контурах оптимальный (критический) коэффициент связи численно равен затуханию любого из связанных контуров.