4.2.1. Примеры расчета частотных характеристик

Пример 1. Для обобщенной одноконтурной цепи, представленной комплексной схемой замещения (рис. 4.8), рассчитать ее частотные характеристики:

Z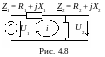 _вх(j), Z_вх(), _Z();

K(j), K(), _K().

Решение. По определению Z_вх(j) =  . Используя законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления:

Z _вх(j) = U_1m/I_1m = I_1m(Z₁ + Z₂); I_1m = (R₁+R₂) + j(X₁+X₂) = R + jX;

;

Используя определение K_u(j) и законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ коэффициента передачи по напряжению:

П ример 2. Для интегрирующей RC-цепи, изображенной на рис. 4.9, рассчитать:

z_вх(j), z(), _z();

K_u(j), K(), _K().

От исходной цепи переходим к ее комплексной схеме замещения. Она соответствует схеме на рис. 4.8.

Используя определение z_вх(j) и законы Ома и Кирхгофа, получим его выражение

О пределим АЧХ и ФЧХ для z_вх(j) и построим их графики (рис. 4.10), подсчитав значения при  = 0,  = :

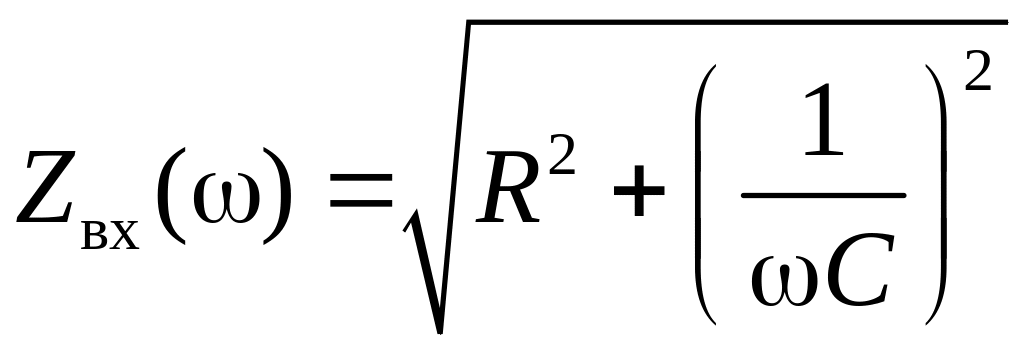; Z_вх(0) = ; Z_вх() = R.

_z() = – arctg ; _z(0) = –/2; _z() = 0.

Используя определение K_u(j), получим его выражение

K_u(j)= = = = .

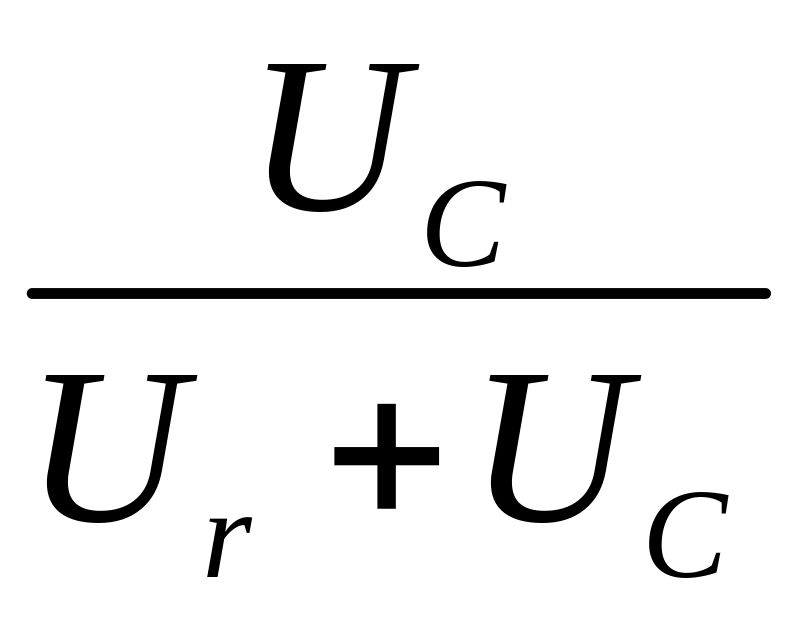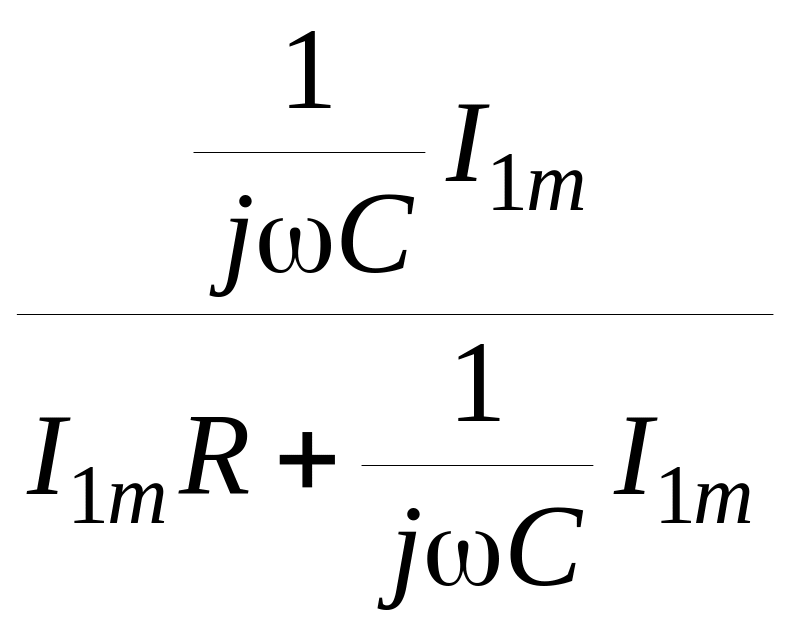Определим АЧХ и ФЧХ для K_u(j) и построим их графики (рис. 4.11), подсчитав значения при  = 0,  = .

Учитывая, что

Z = = ,

где 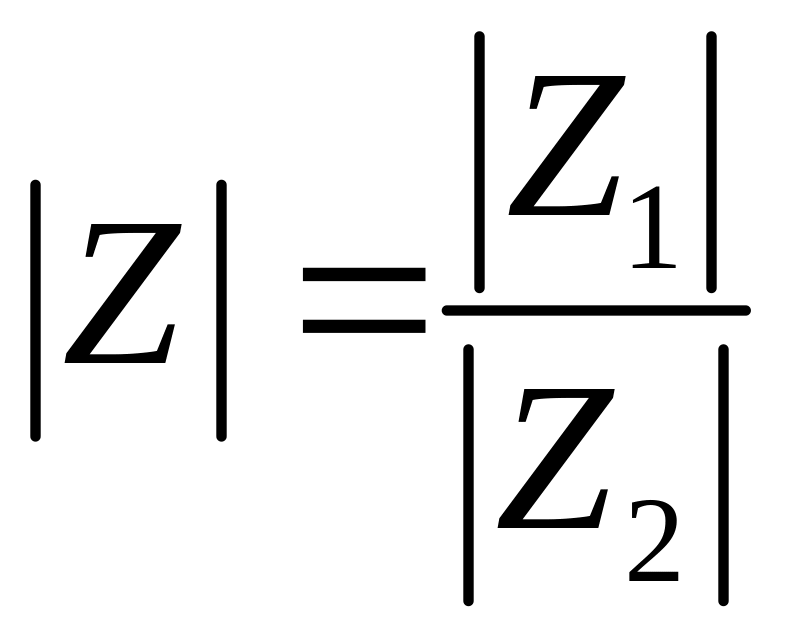, . Тогда

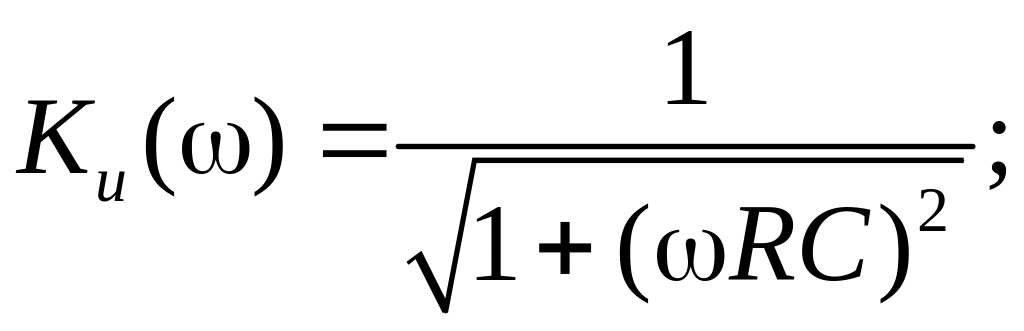K_u(0) = 1; K_u() = 0.

.

Отсюда следует

φ_K() = –π/2, φ_K(0) = 0.

Такая цепь пропускает сигналы низких частот (K_u(0) = 1) и подавляет сигналы высоких частот (K_u() = 0), т.е. является фильтром низких частот (ФНЧ).

Граничная частота определяется из выражения . Рассчитаем ее для нашего примера:

; _грRC =1  .

Построим годограф передаточной функции (график АФЧХ К_u).

П ри .

При .

Учитывая, что реальная часть всегда положительна и уменьшается от 1 до 0, а мнимая часть всегда отрицательна, можно построить график годографа (рис. 4.12).

П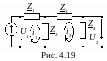 ример 3. Для обобщенной двухконтурной цепи, представленной комплексной схемой замещения (рис. 4.19), рассчитать ее частотные характеристики:

Z_вх(j), Z_вх(), _z(), K(j), K(), _K().

Решение. Найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления.

По определению, Z_вх(j) =  . Входное сопротивление находим методом последовательных эквивалентных преобразований (рис. 4.20).

U₁

U₂

Z₁

Z₂

Z₃₄

U₁

U₂

U₂

U₁

Z₁

Z₂₃₄

Z₁₂₃₄

а б в Рис. 4.20

н айдем КЧХ коэффициента передачи по напряжению. По определению, K_u(j) = U_2m/U_1m, а U_2m = Z₄İ₂ находим по закону Ома.

Отсюда видно, что для расчета КЧХ необходимо найти İ₂. Находим İ₂ методом контурных токов. Для этого определим число независимых контуров: N_k = b – у + 1 = 3 – 2 + 1 = 2, каждому из них присвоим свой контурный ток İ₁, İ₂ и составим уравнения по методу контурных токов.

Z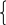 ₁₁İ₁ + Z₁₂İ₂  = E₁₁; Z₂₁İ₁ + Z₂₂İ₂  = E₂₂ ,

где Z₁₁ – собственное сопротивление первого контура, Z₁₁ = Z₁+Z₂;

Z₁₂ и Z₂₁ – сопротивление смежных контуров, Z₁₂ = Z₂₁ = –Z₂;

Z ₂₂ – собственное сопротивление второго контура, Z₂₂ = Z₂+Z₃+Z₄;

Ė₁₁ – алгебраическая сумма источников ЭДС первого контура, Ė₁₁ = U_1m;

Ė₂₂ – алгебраическая сумма источников ЭДС второго контура, во втором контуре источников ЭДС нет, Ė₂₂ = 0.

Найдем İ₂ – ток второго контура (по методу Крамера), а затем и КЧХ коэффициента передачи по напряжению:

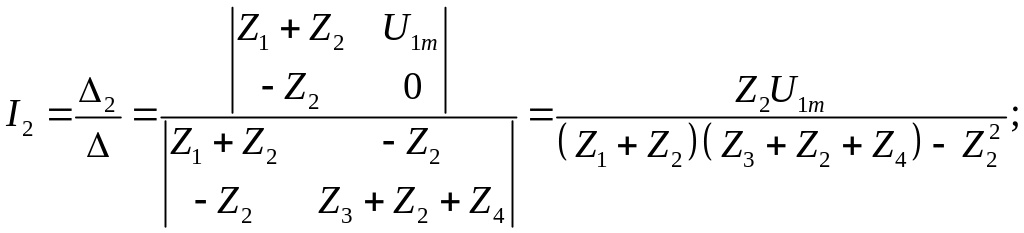
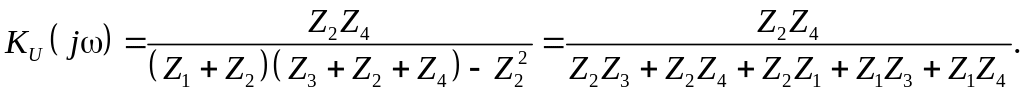
Н айдем КЧХ другим способом, используя для расчета U_2m метод узловых потенциалов. Для этого:

• преобразуем исходную схему к виду, показанному на рис. 4.21, заменив источник ЭДС на источник тока;

• потенциал узла 0 примем равным нулю, ₀ = 0.

Тогда , _.

Составив уравнения по методу узловых потенциалов, получим систему второго порядка и решим ее относительно ₂ по методу Крамера:

Y ₁₁₁ + Y₁₂₂   = İ₁₁; Y₂₁₁ + Y₂₂₂  = İ₂₂,

где Y₁₁ – собственная проводимость первого узла, Y₁₁ = (1/Z₁)+(1/Z₂)+(1/Z₃);

Y₁₂ и Y₁₂ – межузловая проводимость Y₁₂ = Y₂₁ = –1/Z₃;

Y₂₂ – собственная проводимость второго узла Y₂₂ = (1/Z₃) + (1/Z₄);

_1, ₂ – потенциалы первого и второго узлов;

İ_11, İ₂₂ – токи источников токов, сходящихся в первом и втором узлах.

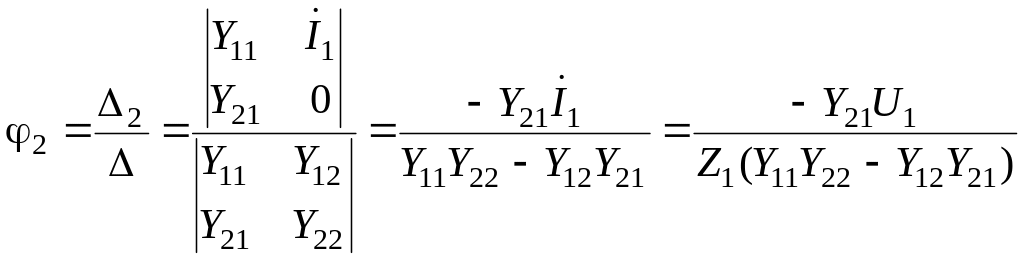
Отсюда следует, что

Для построения ФЧХ необходимо пользоваться следующими формулами:

, где a – реальная часть, а b – мнимая (рис. 5.16). Φ_Z =

I a > 0, b > 0; φ = arctg ;

II a < 0, b > 0; φ = – arctg ;

III a < 0, b < 0; φ = + arctg ;

IV a > 0, b < 0; φ = – arctg .