4.2. Частотные характеристики

Поскольку сопротивления элементов цепей зависят от частоты, то параметры цепей оказываются частотно-зависимыми. Зависимости параметров цепей от частоты называют частотными характеристиками (ЧХ), или частотными функциями цепи.

Каждый параметр цепи имеет свою частотную характеристику. Название ЧХ дают в соответствии с названием параметра, например ЧХ входного сопротивления, ЧХ коэффициента передачи напряжения.

Комплексная ЧХ (КЧХ) есть зависимость от частоты отношения комплексной амплитуды отклика к комплексной амплитуде воздействия. Как всякую комплексную функцию ее можно записать в одной из трех форм записи: показательной, алгебраической и тригонометрической (применяется редко).

,

где , – реальная и мнимая составляющие КЧХ электрической цепи. H(ω) = Y_m/X_m – амплитудно-частотная характеристика (АЧХ), это модуль комплексной функции:

mod [H(jω)] = H() = .

АЧХ есть зависимость от частоты отношения амплитуды гармонического сигнала на выходе к амплитуде гармонического сигнала на входе (без учета начальных фаз).

() = _y – _x – фазо-частотная характеристика (ФЧХ), или аргумент комплексной функции – arg[H(jω)] = .

ФЧХ есть зависимость от частоты сдвига по фазе между выходным и входным сигналами.

Для наглядности ЧХ цепей представляют в графическом виде.

Расчет и построение частотных характеристик

Численный расчет проводят по аналитическим выражениям АЧХ, ФЧХ, АФХ. В качестве переменной используется циклическая частота f. Результаты вычислений приводят в таблице:

Частота, f	Модуль H(f)	Аргумент (f)	Re[Н(jω)]	Im[Н(jω)]

Расчет частотных характеристик всегда проводят в определенном (ограниченном) диапазоне частот, в котором проявляются основные частотные свойства электрической цепи. Величину диапазона частот можно оценить с помощью особых точек (нулей и полюсов) операторной передаточной функции H(p), которая получается из частотной передаточной функции заменой мнимой переменной jω на комплексную переменную :

В качестве нижней граничной частоты f_н можно принять значение, близкое к величине где – расстояние от начала координат до ближайшей особой точки (нуля p₀ или полюса p_*), т.е. модуль особой точки, ближайшей к началу координат: S = p₀ или S = p_*.

За верхнюю граничную частоту f_В можно взять значение

где S_max – расстояние от начала координат до самой удаленной особой точки.

Графически частотные характеристики можно представить в двух формах:

1. В виде двух графиков – АЧХ и ФЧХ. При построении графиков АЧХ и ФЧХ пользуются следующими масштабами по осям: линейным и логарифмическим. Если диапазоны изменения частоты по оси абсцисс и функции (коэффициент передачи) по оси ординат составляют два и более порядков, то пользуются логарифмическим масштабом по двум осям. Если диапазон изменения одной величины (частоты или функции) не больше двух порядков, то пользуются полулогарифмическим масштабом (по одной оси линейный масштаб). Если диапазоны частоты и функции не превышают двух порядков, то график изображают в линейном масштабе.

На рис. 4.6, а приведен график в линейном масштабе, на рис. 4.6, б – в полулогарифмическом, а на рис. 4.6, в – в двойном логарифмическом масштабе.

­

H()

H()

lgH()

10⁵ 10⁶ 

10⁵

10⁵

5

0 1 2 3 4 5 6 lg 

0 1 2 3 4 5 6 lg 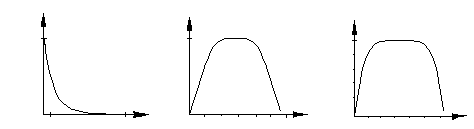

а б в Рис. 4.6

2. В виде графика амплитудно-фазовой частотной характеристики (АФХ), построенной на комплексной плоскости, который называют годографом. Годограф – это геометрическое место точек, которые описывает конец вектора комплексной функции на комплексной плоскости при изменении частоты от 0 до бесконечности.

Д ля построения годографа обычно используют алгебраическую форму записи частотной характеристики Н(jω) = = Re[Н(jω)] + j Im[Н(jω)]. Далее для определенных частот ω_i рассчитывают значения Re[Н(jω)] = Н₁(ω_i) и Im[Н(jω)] = Н₂(ω_i) и составляют таблицу данных для построения АФХ, а затем, как обычно, наносят эти точки на плоскость и, соединив их, получают график годографа (рис. 4.7).