4. Частотные характеристики и операторные функции электрических цепей

4.1. Параметры электрических цепей

Большинство электрических цепей служат средством связи для передачи сигналов от источника сигнала в нагрузку (рис. 4.1), где x(t) – сигнал на входе цепи. Он называется входным сигналом, или воздействием; y(t) – выходной сигнал, или отклик:

y(t) = F(x(t), a, b, c).

Рис. 4.1

Когда схема электрической цепи неизвестна, недоступна или нас не интересует, ее изображают в виде прямоугольника с рядом выводов (полюсов) схемы, с помощью которых она соединяется с другими устройствами.

1. В зависимости от числа выводов (полюсов) электрические цепи делятся на двухполюсники, четырехполюсники, многополюсники (рис. 4.2)

1

1¹

1

1

1

2¹

2

2

2

n

Рис. 4.2

2. В зависимости от наличия в цепях активных элементов различают пассивные и активные цепи. Активные цепи содержат источники (активные элементы), а пассивные их не содержат. Активные цепи делят на автономные и неавтономные. Автономные цепи содержат независимые источники, а неавтономные содержат только зависимые источники.

В общем случае связь между откликом и воздействием имеет вид дифференциального уравнения. Если цепь линейная, то уравнение линейное, где a, b, c – параметры элементов, входящих в цепь.

Если входной сигнал гармонический, то его представляют комплексной амплитудой.

→ .

Если цепь линейная, то откликом такой цепи является гармонический сигнал с комплексной амплитудой

.

Причем связь между комплексной амплитуды отклика и воздействия имеет вид линейного алгебраического уравнения:

, ,

где H (a, b, c) – параметр электрической цепи (это комплексное число).

Параметр цепи есть отношение комплексной амплитуды отклика к комплексной амплитуде воздействия.

4.1.1. Параметры двухполюсника

Двухполюсником является цепь с двумя выводами рис. 4.2. Его режим работы характеризуется двумя величинами

1. Если воздействием считать амплитуду тока, то откликом будет являться напряжение на нем.

По закону Ома: , где Z – сопротивление двухполюсника. (Z = R+jX – комплексное число, где R и X – резистивная и реактивная составляющие сопротивления двухполюсника).

Обобщенная схема замещения двухполюсника приведена на рис. 4.3.

2. Если воздействием считаем амплитуду напряжения, тогда откликом будет амплитуда тока, связанная с напряжением:

; ,

г де Y – второй параметр двухполюсника, он называется комплексной проводимостью двухполюсника:

Y = G + jB,

G и B – резистивная и реактивная составляющие проводимости двухполюсника.

Вторая схема замещения двухполюсника приведена на рис. 4.4. Эти схемы замещения при определенном выборе параметров эквивалентны.

4.1.2. Параметры четырехполюсника

Параметры четырехполюсника можно разбить на четыре группы:

1. Входные параметры связывают и :

По отношению к источнику сигнала четырехполюсник является двухполюсником, а поэтому его входные параметры аналогичны параметрам двухполюсника:

, ,

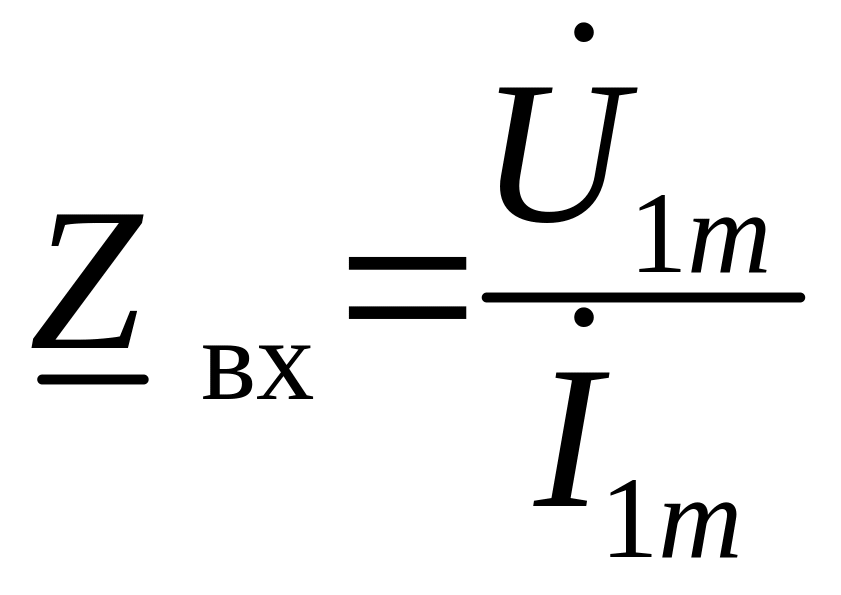где Z_вх – входное сопротивление четырехполюсника; Y_вх – входная проводимость четырехполюсника.

2. Передаточные параметры характеризуют передачу сигнала с входа на выход, или, как говорят, передачу в прямом направлении. Передаточных параметров четыре

; ; ; ,

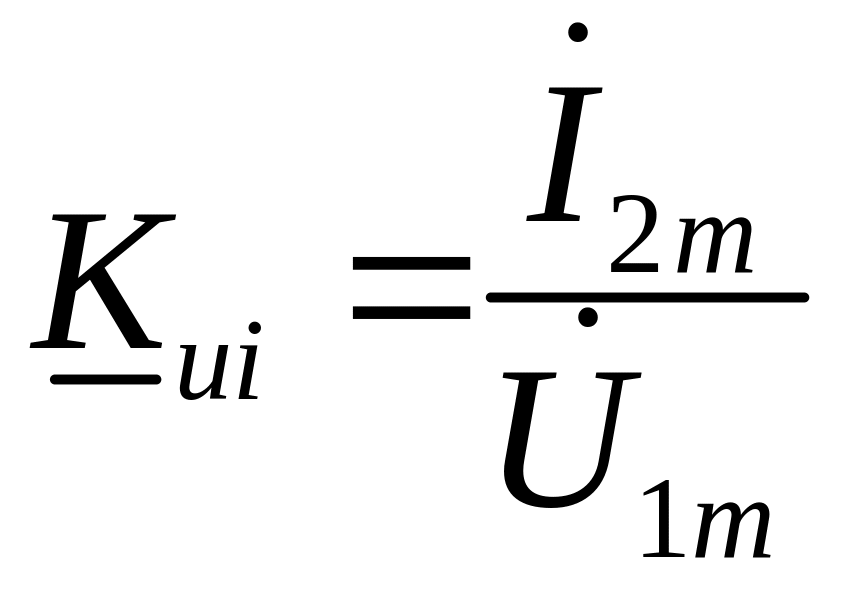где K_u – коэффициент передачи по напряжению;

K_i – коэффициент передачи по току;

K_iu – сопротивление прямой передачи, или коэффициент преобразования ток – напряжение;

K_ui – проводимость прямой передачи, или коэффициент преобразования напряжение – ток.

3. Выходные параметры:

а) Z_вых =  ,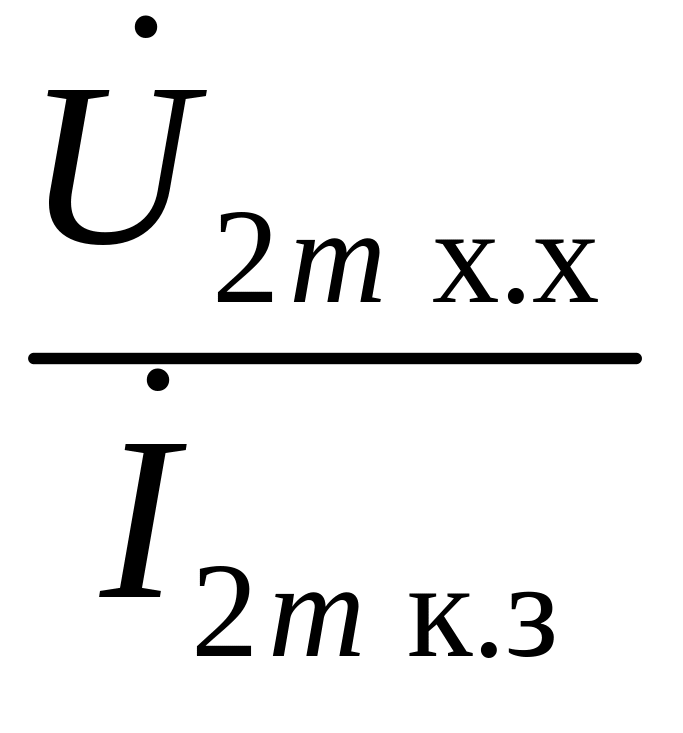

где Z_вых – комплексное выходное сопротивление;

– комплексная амплитуда выходного напряжения в режиме холостого хода (х.х). Холостой ход – это режим, когда выполняются условия: İ_2m = 0, Z_н = ∞;

– комплексная амплитуда выходного тока в режиме короткого замыкания (к.з). Короткое замыкание – это режим, когда Z_н = 0.

б) 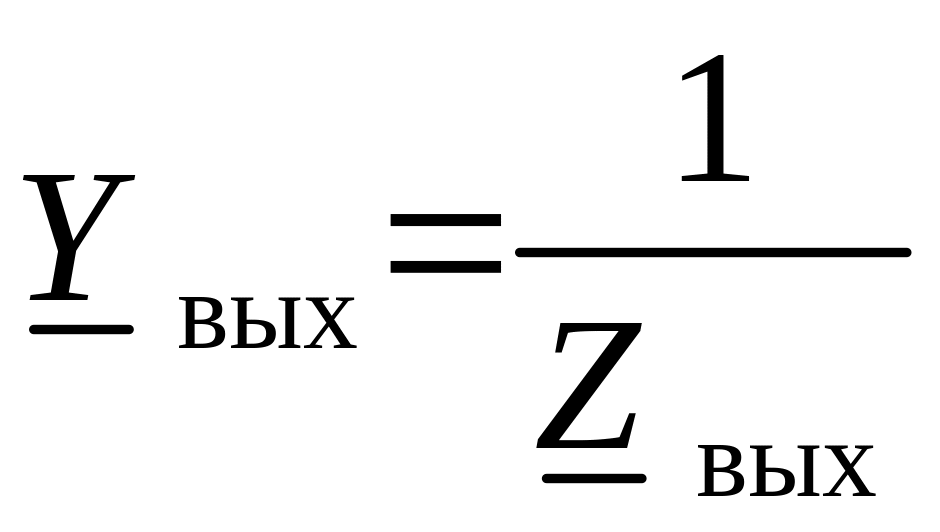– комплексная выходная проводимость.

4. Параметры обратной передачи сигнала. Они характеризуют передачу сигнала с выхода на вход. Таких параметра четыре, и они аналогичны параметрам второй группы: (K_u, K_i, K_iu, K_ui).