3.4. Эквивалентные преобразования электрических цепей

Часто исходная электрическая схема состоит из большого числа элементов и представляет интерес замены ее другой, более простой – состоящей из меньшего числа элементов, но эквивалентной исходной. Такая замена называется одной цепи другой называется преобразованием цепи. Преобразования электрических цепей считают эквивалентными, если при их выполнении напряжения и токи на интересующих нас участках не изменяются.

Электрические цепи считают простыми, если они содержат только последовательное или только параллельное соединение элементов.

Участок цепи, содержащий и параллельное, и последовательное соединение элементов называют сложным или участком со смешанным соединением элементов.

При преобразовании сложных электрических цепей пользуются последовательным методом, то есть последовательно преобразуют участки цепи, имеющие простое соединение элементов.

3 .4.1 Эквивалентное преобразование схемы при последовательном соединении элементов

Рассмотрим комплексную схему замещения электрической цепи, состоящей из последовательного соединения отдельных элементов (рис. 3.7). Данная цепь представляет собой контур, у которого через все элементы протекает общий для всех элементов ток. Эквивалентно преобразуем схему к одному элементу, но так, чтобы напряжение и ток на выводах схемы сохранили свои значения. На основании закона Ома и второго закона Кирхгофа в комплексной форме можно записать уравнение электрического равновесия

.

Отсюда напряжение и ток для обеих схем одинаковы когда

.

Вывод. При эквивалентном преобразовании при последовательном соединении элементов их комплексные сопротивления складываются.

1) Эквивалентное преобразование сопротивлений.

Р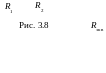 ассмотрим электрическую цепь, схема которой приведена на рис.3.8. Эквивалентно преобразуем сопротивления R₁ и R₂ к одному сопротивлению R_экв.

Учитывая, что Z_R = R, и полученное соотношение, имеем R_экв = R₁ + R₂.

2) Эквивалентное преобразование емкостей.

Рассмотрим электрическую цепь, схема которой приведена на рис.3.9. Эквивалентно преобразуем емкости С₁ и С₂ к одной эквивалентной емкости С_экв.

У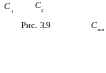 читывая, что Z_С = 1/(jωC), и полученное соотношение, имеем

.

3) Эквивалентное преобразование индуктивностей.

Р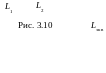 ассмотрим электрическую цепь схема, которой приведена на рис.3.10. Эквивалентно преобразуем индуктивности L₁ и L₂ к одной эквивалентной индуктивности L_экв.

Учитывая, что Z_L = jωL, и полученное соотношение, имеем L_экв = L₁ + L₂.

3.4.2 Эквивалентное преобразование схемы при параллельном соединении элементов

Р ассмотрим комплексную схему замещения электрической цепи, состоящей из параллельного соединения отдельных элементов (рис. 3.11). Данная цепь содержит два узла, между которыми включены все элементы. Общим для всех элементов является напряжение на них. Эквивалентно преобразуем схему к одному элементу, но так, чтобы напряжение и ток на выводах схемы сохранили свои значения. На основании закона Ома и первого закона Кирхгофа в комплексной форме можно записать уравнение электрического равновесия

I = I₁+I₂+…+I_n, или (U/Z_экв) = (U/Z₁) + (U/Z₂) + … +(U/Z_n) .

Отсюда следует, что

(1/Z_экв) = (1/Z₁) + (1/Z₂) + … +(1/Z_n), или Z_экв = 1/[(1/Z₁) + (1/Z₂) + … +(1/Z_n)].

Учитывая, что (1/Z) = Y – комплексная проводимость элемента, можно записать

Y_экв = Y₁ + Y₂ + … + Y_n.

Вывод. При эквивалентном преобразовании при параллельном соединении элементов их комплексные проводимости складываются.

1) Эквивалентное преобразование сопротивлений.

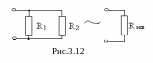Рассмотрим электрическую цепь, схема которой приведена на рис. 3.12. Эквивалентно преобразуем сопротивления R₁ и R₂ к одному сопротивлению R_экв.

Учитывая, что Z_R = R, и полученное соотношение, получим R_экв = R₁R₂/(R₁+R₂).

2) Эквивалентное преобразование емкостей.

Р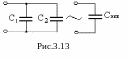 ассмотрим электрическую цепь, схема которой приведена на рис. 3.13. Эквивалентно преобразуем емкости С₁ и С₂ к одной эквивалентной емкости С_экв. Учитывая, что Z_С = 1/(jωC), и полученное соотношение, имеем C_экв = C₁ + С₂ .

3) Эквивалентное преобразование индуктивностей.

Р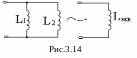 ассмотрим электрическую цепь, схема которой приведена на рис. 3.14. Эквивалентно преобразуем индуктивности L₁ и L₂ к одной эквивалентной индуктивности L_экв.

Учитывая, что Z_L = jωL, и полученное соотношение, имеем L_экв = L₁L₂/(L₁+L₂).