1.3 Математические модели элементов электрических цепей

Любая электрическая цепь состоит из отдельных элементов, в которых при протекании электрического тока происходят достаточно сложные энергетические явления, связанные с преобразованием энергии. Для упрощения описания процессов, происходящих в реальных элементах, их считают идеализированными, т.е. предполагают, что каждый идеализированный элемент обладает лишь одним каким-либо свойством: либо поглощать или накапливать электрическую или магнитную энергию (это – пассивные элементы), либо создавать (это – активные элементы).

Классификация идеализированных элементов электрических цепей дана на рис. 1.3.

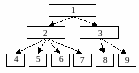
Рис. 1.3. 1 – элементы электрических цепей, 2 – пассивные элементы, 3 – активные элементы, 4 – сопротивление, 5 – емкость, 6 – индуктивность, 7 – взаимно-индуктивная цепь, 6 – источник тока, 8 – источник ЭДС.

К пассивным идеализированным элементам схемы при переменных токах относятся резистивный элемент с сопротивлением R, или, короче, сопротивление R (иногда его называют активное сопротивление), индуктивный элемент с индуктивностью L, или, короче, индуктивность L, емкостный элемент с емкостью С, или, короче, емкость С, а также взаимно- индуктивный элемент с взаимной индуктивностью М между индуктивными элементами.

1.3.1 Идеализированные пассивные элементы

Существует три основных способа описания свойств элементов электрических цепей:

1. Аналитический способ – в виде электрической характеристики (уравнения) элемента. Это зависимость между физическими величинами, определяющими принцип работы элемента. Например, для сопротивления I = U/R (рис.1.4).

2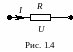 . Графический способ – это график аналитического выражения электрической характеристики. Например, для сопротивления эта вольт-амперная характеристика (ВАХ) приведена на рис. 1.5.

3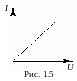 . Параметрический – здесь свойства элемента задаются параметром элемента, который определяется из электрической характеристики:

, например ,

где воздействие – электрическая величина, которая воздействует на элемент; отклик появляется в результате воздействия. Параметр элемента есть отношение отклика к воздействию. В зависимости от характера входного сигнала различают три вида параметров: статические, дифференциальные и комплексные.

Рассмотрим подробнее свойства идеальных элементов электрических цепей.

1. Сопротивление

Сопротивление – идеализированный элемент, которому свойственно только поглощение электрической энергии с преобразованием ее в тепловую, механическую или другую форму. Условное обозначение сопротивления приведено на рис.1.6.

Рассмотрим основные характеристики сопротивления.

1 . Электрическая характеристика идеального сопротивления устанавливает зависимость между током I и напряжением U на этом участке, т.е. I=F(U). Эта зависимость называется вольтамперной характеристикой (ВАХ) и в простейшем случае является линейной, т.е. имеет вид

.

Это фактически Закон Ома для постоянного тока.

2. Параметром сопротивления является величина, которая есть отношения отклика к воздействию, ее обозначают буквой R=U/I и называют сопротивлением. Единица измерения сопротивления – Ом. Часто применяют кратные единицы: 10³ Ом = 1кОм (килоОм), 10⁶ Ом = 1МОм (мегаОм), 10⁹ Ом = 1 ГОм (гигаОм). Иногда вместо сопротивления пользуются параметром, который называется проводимостью: G = 1/R. Единица измерения проводимости – сименс [См].

3. Закон Ома для мгновенных значений токов и напряжений на участке цепи, обладающем сопротивлением:

4. Мгновенная мощность:

,

т.е. сопротивление в любой момент времени поглощает электрическую энергию.

5. Реальным элементом, приближающимся по своим свойствам к сопротивлению, является резистор. Он представляет собой объем проводника (рис. 1.8) с высоким удельным сопротивлением ρ. Его основным параметром является сопротивление. Оно рассчитывается по формуле

,

где ρ – удельное сопротивление проводника, т.е. сопротивление проводника с единичными по длине гранями, l – длина проводника, S – площадь поперечного сечения.

2. Емкость

Е мкость – это идеализированный элемент электрической цепи, способный накапливать и отдавать энергию электрического поля.

Условное обозначение приведено на рис.1.9.

1. Зависимость накопленного заряда q в емкости от величины приложенного напряжения u_C , называемая кулон-вольтной характеристикой имеет в общем случае нелинейный характер. Количественно этот элемент оценивают значениями статической и динамической емкости:

, [Ф].

В случае линейной зависимости С_ст = С_дин = С.

Единица измерения емкости – фарада [Ф]=Кл/В. Часто пользуются единицами, которые составляют доли от фарады: 10^–3 Ф = 1мФ (миллифарада); 10^–6 Ф =1мкФ (микрофарада); 10^–9 Ф = 1 нФ (нанофарада); 10^–12 Ф = 1 пФ (пикофарада).

2. Связь между мгновенными значениями тока и напряжения получаем из электрической характеристики, учитывая, что dq=i_cdt=Cdu_c:

.

Разрешим это уравнение относительно u_С(t), получим

,

Если при t = 0 ток мгновенно изменяет свое значение, напряжение на емкости мгновенно измениться не может, оно изменяется непрерывно:

,

где U_C(+0) – напряжение на емкости сразу после скачка тока; U_C(–0) – напряжение на емкости до скачка тока через емкость;

Это соотношение называется законом коммутации для емкости.

3. Мгновенная мощность:

.

Если , то емкость накапливает электрическую энергию, забирая энергию от источника сигнала, напряжение на емкости возрастает, поэтому говорят, что емкость заряжается.

Если , то емкость возвращает энергию в цепь, т.е. сама является источником энергии, которую накопила, напряжение при этом на емкости уменьшается, и говорят, что емкость разряжается.

Благодаря способности емкости накапливать и возвращать энергию в цепь ее называют емкость реактивным элементом.

4. Энергия, запасаемая емкостью W – это энергия электрического поля, создаваемого напряжением u_c, поэтому W=0 при u_c=0. В любой момент времени

.

Процесс запасания энергии в электрическом поле является обратимым. Запасенная энергия может быть отдана другим элементам цепи. Например, энергия заряженного конденсатора при разряде его на сопротивление рассеивается в этом сопротивлении; разряжающийся конденсатор можно рассматривать в указанном смысле как активный элемент — источник энергии.

5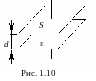 . Реальным элементом, приближающимся по своим свойствам к емкости, является конденсатор, его основным параметром является емкость. В простейшем случае он представляет собой две металлические пластины, разделенные диэлектриком (рис.1.10).

Емкость такого конденсатора определяется выражением: ,

где ε – диэлектрическая проницаемость, S – площадь пластины, d – расстояние между пластинами.

3. Индуктивность

Индуктивность – идеализированный элемент, который способен накапливать и отдавать энергию магнитного поля.

Н аиболее близким к этому идеализированному элементу является реальный элемент – индуктивная катушка. Она представляет собой спираль (рис. 1.11), выполненную из ряда витков тонкого провода; основным ее параметром является индуктивность.

У словное обозначение индуктивности приведено на рис. 1.12. Рассмотрим основные свойства индуктивного элемента.

Связь между напряжением и током в индуктивной катушке определяется законом электромагнитной индукции, из которого следует, что при изменении магнитного потока, пронизывающего индуктивную катушку, в ней наводится ЭДС, пропорциональная скорости изменения потокосцепления катушки и направленная таким образом, чтобы вызываемый ею ток стремился воспрепятствовать изменению магнитного потока:

.

Потокосцепление катушки равно алгебраической сумме магнитных потоков, пронизывающих ее отдельные витки.

1. Электрическая характеристика индуктивного элемента устанавливает зависимость между током I, протекающим по элементу и потокосцеплением катушки ψ, возникающим при этом, т.е. ψ=f(I) (Вб=Вс). Эта зависимость называется вебер-амперной характеристикой. В простейшем случае она имеет линейный характер:

.

2. Основным параметром индуктивного элемента является индуктивность, которая есть отношения отклика к воздействию, т.е.:

.

Ее единица измерения– генри [Гн]. (Гн = Омс)

3. Ток и напряжение на линейном индуктивном элементе связаны соотношением:

.

Если ток постоянный, то .

Разрешим это уравнение относительно тока

.

Если при t = 0 напряжение на индуктивности мгновенно возрастает, ток мгновенно измениться не может:

,

где I_L(–0) – ток через индуктивность до коммутации, I_L(+0) – ток через индуктивность после коммутации.

Это соотношение называют законом коммутации для индуктивности.

4. Мгновенная мощность:

.

Если p(t) > 0, то индуктивность накапливается энергия; если p(t) < 0, то происходит отдача энергии.

5. Энергия, которую запасает индуктивный элемент в магнитном поле, определятся величиной тока:

,

Индуктивность зависит от параметров витка, от шага намотки, от числа витков, от магнитной проницаемости материала (сердечника), введенного в катушку.

4. Индуктивно связанный элемент, идеальный трансформатор

И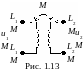 деальный трансформатор служит для преобразования (трансформации) переменного тока одного напряжения в переменный ток другого напряжения. Он состоит из двух индуктивно связанных катушек индуктивности (рис. 3.13), слева расположена первичная катушка индуктивности, справа – вторичная катушка индуктивности.

L₁ – первичная индуктивность, L₂ – вторичная индуктивность, M – коэффициент взаимной индуктивности.

Напряжения и токи в этом элементе связаны следующими отношениями:

, .

Каждое из напряжений состоит из двух слагаемых: первое обусловлено током через данную индуктивность, второе – через соседнюю.

Знак у второго слагаемого зависит от направления токов в индуктивностях, если токи направлены одинаково, в одном направлении (такое включение называется согласованным), то берется знак плюс, если токи направлены встречно (встречное включение), то берется знак минус.

Идеальный трансформатор – это такой элемент электрической цепи, который передает энергию без ее потери, т.е.

р₁ = u₁ i₁ = p₂ = u₂ i₂,

где p₁ – мощность, подводимая к первичной индуктивности, р₂ – мощность, отбираемая от вторичной индуктивности. В идеальном трансформаторе не происходит потери энергии при передаче сигнала через него. Напряжения u₁ и u₂ и токи i₁ и i₂ связаны соотношениями:

u₂ = n u₁, i₂ = i₁/n,

где n – коэффициент трансформации. Он равен отношению числа витков вторичной обмотки w₂ к числу витков первичной ω₁:

n=w₂/w₁.

Е сли n > 1, то такой трансформатор называется повышающим (напряжение). Если n < 1, т.е. число витков во вторичной обмотке меньше, чем в первичной, то такой трансформатор называется понижающим (напряжение).

У реального трансформатора p₂ < p₁. Он представляет собой несколько обмоток, размещенных на общем замкнутом сердечнике, выполненном из магнитомягкого материала для увеличения магнитной связи (рис. 1.14.).