4. Затухающие колебания механической системы.
В
любой реальной колебательной системе
есть силы, препятствующие свободным
колебаниям. При этом часть энергии
системы безвозвратно теряется и колебания
постепенно затухают. Следовательно,
реальные свободные колебания всегда
являются затухающими.
В общем случае для механических колебаний
сила сопротивления может быть записана
как
 ,
где r – коэффициент сопротивления,
а знак «-» обозначает, что
,
где r – коэффициент сопротивления,
а знак «-» обозначает, что
 противоположны по направлению. Тогда
основное уравнение динамики для
материальной точки запишется как
противоположны по направлению. Тогда
основное уравнение динамики для
материальной точки запишется как
 и, введя обозначение
и, введя обозначение
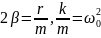 , получим дифференциальное
уравнение, описывающее затухающие
механические колебания материальной
точки:
, получим дифференциальное
уравнение, описывающее затухающие
механические колебания материальной
точки:
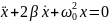
Его
решение:
 .
Периодичность нарушается
.
Периодичность нарушается
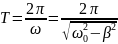 ;
;
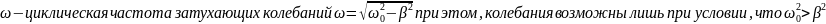 .
.
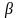 -
коэффициент затухания,
-
коэффициент затухания,
 -
собственная (циклическая) частота, А –
амплитуда затухающих колебаний,
уменьшающаяся со временем по
экспоненциальному закону А
=
-
собственная (циклическая) частота, А –
амплитуда затухающих колебаний,
уменьшающаяся со временем по
экспоненциальному закону А
=

Затухающие электромагнитные колебания.
В реальном колебательном контуре часть энергии идет на выделение джоулева тепла в проводниках и активном сопротивлении катушки индуктивности. Следовательно, свободные колебания в контуре затухают тем быстрее, чем больше его активное сопротивление. Если выделить все активные сопротивления контура в виде R, то для реального колебательного контура (при условии I>0 при зарядке С)


 +
+
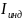 -
-

 -
IR -
-
IR -
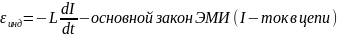
C
 + L
+ L
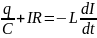
+
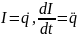
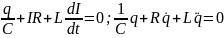

Введем
обозначения:
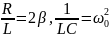 получаем уравнение для изменения со
временем заряда q
:
получаем уравнение для изменения со
временем заряда q
:
 -
коэффициент затухания,
-
собственная (циклическая) частота, q
– заряд на конденсаторе,
-
коэффициент затухания,
-
собственная (циклическая) частота, q
– заряд на конденсаторе,
Это уравнение совпадает по виду с дифференциальным уравнением затухающих механических колебаний.
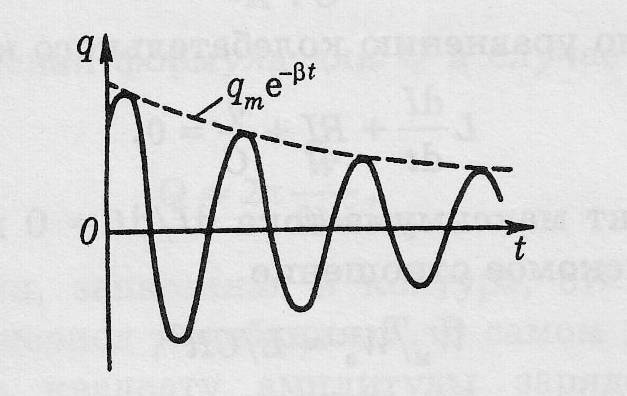
Его
решение (из теории дифференциальных
уравнений):


 ,
таким
образом, частота затухающих колебаний
(циклическая)
,
таким
образом, частота затухающих колебаний
(циклическая)
 т.е.
т.е.
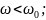
Для U и I получим:


Введем
обозначение
 ,
,
 ,
,
Тогда
 (Вспомним,
что
(Вспомним,
что
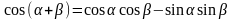 )
)
График функции для зависимости q от времени имеет вид
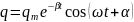
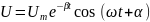

 -
сдвиг
фаз между током и напряжением
-
сдвиг
фаз между током и напряжением
Для характеристики затухания колебаний в контуре вводят понятие логарифмического декремента затухания.

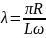
Физический
смысл логарифмического декремента
затухания
 .
.
Логарифмический декремент затухания – величина, обратная числу колебаний Ne , после совершения которых амплитуда колебаний уменьшается в е раз. Другой важной характеристикой контура является его добротность Q.

Добротность-
это умноженное на
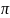 число колебаний Ne
,
после совершения которых амплитуда
колебаний уменьшается в е раз.
Введем новое обозначение:
число колебаний Ne
,
после совершения которых амплитуда
колебаний уменьшается в е раз.
Введем новое обозначение:
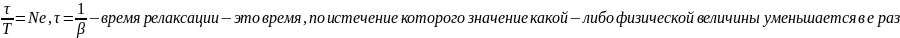
В
случае слабого затухания колебаний
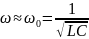 .
.

Вынужденные колебания.
Колебания в системе, вызванные внешним периодически изменяющимся воздействием, называются вынужденными.
Рассмотрим колебательный контур, в который последовательно включен источник переменного напряжения. Uc , UL , UR - напряжения, соответственно, на конденсаторе С, на катушке индуктивности L(на схеме не изображена) и на омическом сопротивлении контура R.
+ -


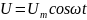
+ I
+
 –
–


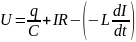




Получили
дифференциальное уравнение вынужденных
колебаний
Решение
этого дифференциального уравнения
представляет собой сумму общего решения
однородного уравнения и частного решения
неоднородного q=q1+q2.
Нас будут интересовать только
установившиеся колебания. Поскольку в
общем решении
 стоит
множитель
стоит
множитель
 ,
быстро убывающий со временем, то
вынужденные колебания практически
описываются частным решением
дифференциального уравнения q2,
которое может быть представлено в виде:
,
быстро убывающий со временем, то
вынужденные колебания практически
описываются частным решением
дифференциального уравнения q2,
которое может быть представлено в виде:


Или с учетом ранее введенных обозначений
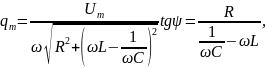

Найдем


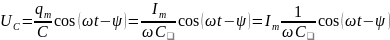 =
=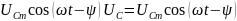


Введем
обозначение
 , откуда
, откуда
 (*)
(*)
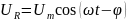 - в
фазе с током
- в
фазе с током
 -
отстает по фазе от тока на
-
отстает по фазе от тока на


 -
опережает ток по фазе на
-
опережает ток по фазе на
Это
может быть представлено с помощью
векторной диаграммы, если изобразить
амплитуды напряжений
URm
=
RIm,
UCm
=
Im
/
 ,
ULm
=Im
,
ULm
=Im
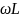 и их векторную сумму, равную
и их векторную сумму, равную

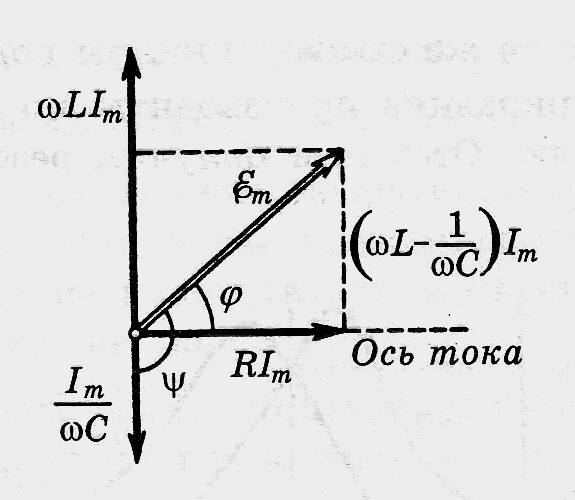
 Определенный
из векторной диаграммы тангенс угла
Определенный
из векторной диаграммы тангенс угла
 соответствует (*). Векторная диаграмма
здесь изображена для внешнего напряжения,
представленного не как как
соответствует (*). Векторная диаграмма
здесь изображена для внешнего напряжения,
представленного не как как
 ,
а как
,
а как
 . Величины:
. Величины:
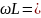 RL
и
RL
и
 =
RC
получили
названия индуктивного RL
и емкостного RC
сопротивлений.
=
RC
получили
названия индуктивного RL
и емкостного RC
сопротивлений.