Лекция Электромагнитные колебания.

1. Общие сведения о колебаниях.

Мы живем в мире движущихся объектов. В зависимости от того, остается ли объект при движении вблизи какого-то положения равновесия или такого положения нет, все виды движения можно свести к двум классам. К первому классу отнесем вибрацию струн музыкальных инструментов, раскачивание качелей и маятника часов, движение груза на пружинных весах и т.п. Примером движений второго колеса являются волны, движущиеся в море к берегу, луч света, движение импульса, возмущения по длинной веревке при дергании за ее конец в вертикальном направлении. Иногда, в зависимости от точки зрения наблюдателя, одно и тоже движение можно отнести к любому из этих классов. Так, поплавок перемещается периодически вверх и вниз, в то время, как волны непрерывной чередой идут к берегу точно также импульс смещения бежит по веревке, а сама веревка не перемещается. Начнем рассмотрение первого класса движений – колебательных движений замкнутых систем, вызванных первоначальным внешним воздействием (возбуждением). Такие колебания называются свободными или собственными. Любая колебательная система описывается некоторой физической величиной, отклонение которой от положения равновесия зависит от координат и времени. Для механических колебаний - это смещение массы от положения равновесия, в случае электрических систем – это электрический ток в катушке индуктивности или заряд и напряжение на пластинах конденсатора. Одними из простейших видов колебаний являются гармонические колебания – колебания при которых значение какой – либо физической величин изменяется с течением временем по закону синуса или косинуса. Любое сложное колебание может быть сведено, в конечном итоге, к наложению нескольких гармонических колебаний.

2. Свободные колебания систем с одной степенью свободы.

Если положение системы в любое время может быть описано единственным параметром, то система имеет одну степень свободы. Этим параметром может быть, например, отрезок прямой, отсчитываемый от некоторой линии или угол, отсчитываемый от какой-то плоскости. Будем считать, что в положении устойчивого равновесия (х=0) потенциальная энергия U=U(x) системы минимальна U(0)=0. В случае малых колебаний, разложив функцию U(x) в ряд по степеням x, ограничимся первыми тремя членами формулы Маклорена: , т.к. 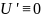в точке минимума , а U'' должна быть >0, то 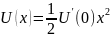. Введя обозначение U'(0)=k (k>0) получаем формулу для потенциальной энергии . Зная вид функции U(x) можно найти величину силы, действующей на систему 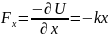. Силы вида называются квазиупругими независимо от их природы. Эта сила (знак «-») всегда направлена к положению равновесия и называется возвращающей силой. Рассмотрим в качестве примера колебательную систему с одной степенью свободы пружинный маятник.

Без нагрузки длина системы:

В положении равновесия: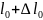

kx

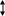
полож. 0 Когда

X равнов. mg

X

В смещенном положении 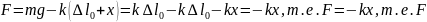действительно носит характер квазиупругой силы.

Если шарик сместить из положения равновесия на x=a и дать ему свободу, то под действием квазиупругой силы F шарик будет двигаться со скоростью 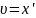. Потенциальная энергия при 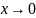будет убывать, а кинетическая энергия должна возрастать (закон сохранения энергии). Массой пружины пренебрегаем. Пройдя положение равновесия движение станет замедляться и при x= - a шарик остановится 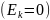. При отсутствии трения получим собственные колебания системы. Основное уравнение динамики поступательного движения записывается в данном случае , обозначив

имеем

.

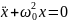Это дифференциальное уравнение описывает собственные колебания системы в отсутствие сил трения. Общее решение этого дифференциального уравнения имеет вид: 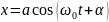, где 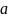-амплитуда колебания, 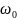- циклическая (круговая) частота, 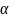- начальная фаза колебания.

Итак, движение системы, находящейся под действием силы вида F=-kx, является гармоническим колебанием.