7.3 Частотные характеристики последовательного резонансного контура

При построении частотных характеристик удобно пользоваться относительными единицами, так как при этом сокращается число параметров и становиться возможным пользоваться стандартными кривыми.

Например, в качестве аргумента вместо частоты ω, может быть взята относительная частота ω/ω₀ , т.е. отношение текущей частоты к резонансной . Кроме того , применяется также относительная расстройка частоты, о которой будет сказано ниже.

Рассмотрение частотных характеристик последовательного контура начнем с зависимостей от относительной частоты комплексного сопротивления контура, отнесенного к сопротивлению r , его модуля и угла аргумента. Согласно (7.Ι) с учетом (7.2) и (7.4)

(7.II)

Соответственно модуль равен:

а аргумент

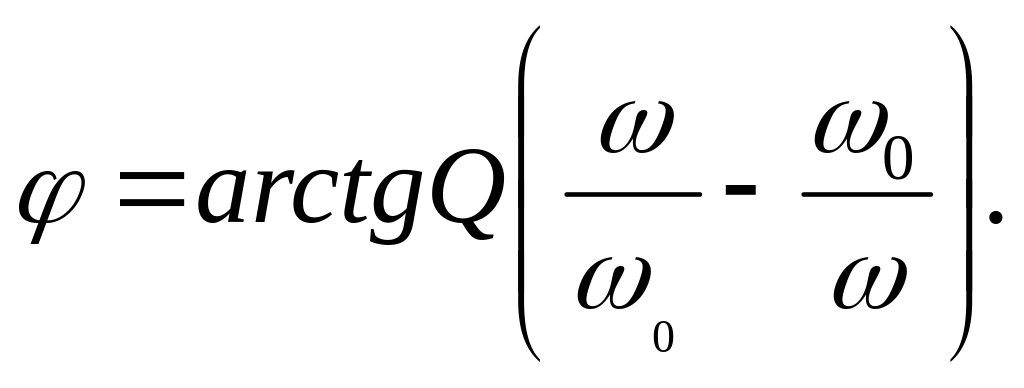
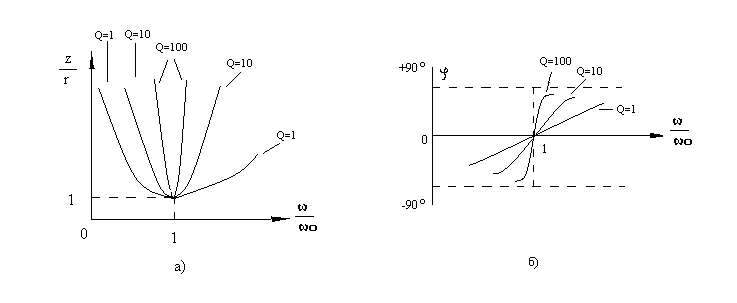
Рис. 7.6 Частотные зависимости относительного сопротивления (а)

и угла (б) фазового сдвига

На рис. 7.6 показаны зависимости z/r и φ от относительной частоты ω/ω_0.

Каждая из этих зависимостей представляет семейство кривых параметра Q.

Семейство кривых z/r проходит через точку с координатами ω/ω₀=I, z/r=I, которая соответствует условию резонанса. Семейство кривых φ проходит через точку ω/ω₀=I, φ= , которая также соответствует резонансу.

Ток в цепи , отнесенный к току I₀ при резонансе, равен

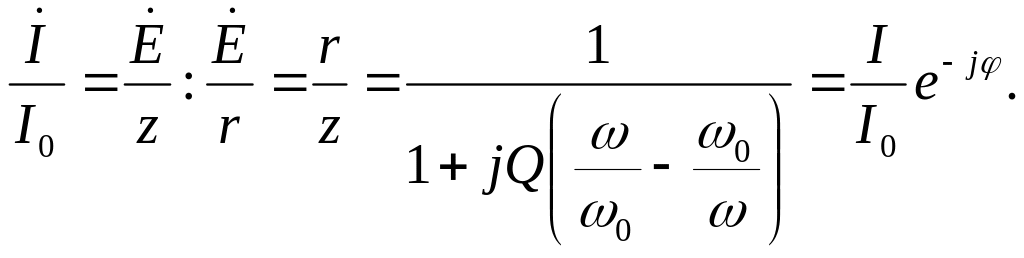(7.I4)

Частотную зависимость модуля 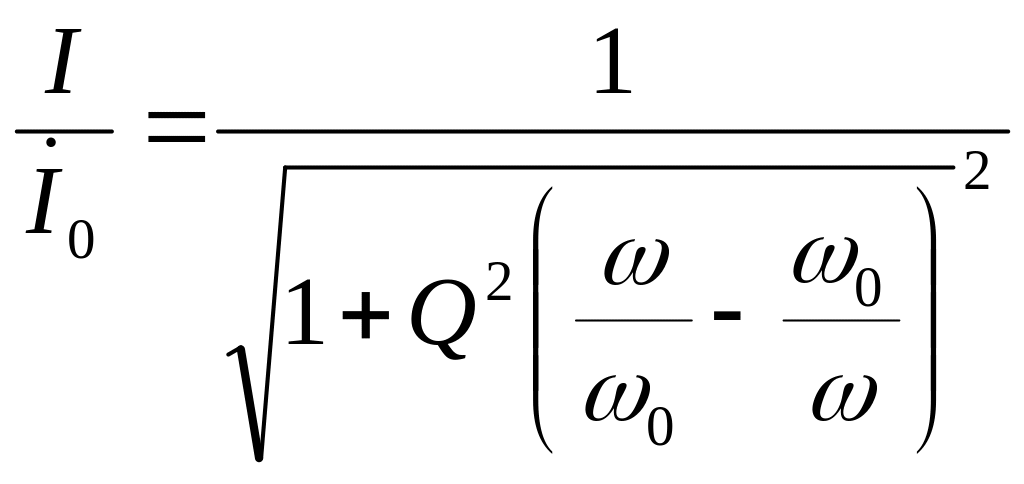(7.I5)

принято называть амплитудно-частотной характеристикой или резонансной кривой тока.

Частотная зависимость угла фазового сдвига тока относительно приложенного напряжения называется фазо-частотной или просто фазовой характеристикой тока; она выражается зависимостью (7-I3).

Положительные значения фазовой характеристики соответствуют отстающему, а отрицательные – опережающему по фазе току.

Как и следовало ожидать, при частотах ниже резонансной, когда емкостное сопротивление преобладает над индуктивным, сопротивление последовательного контура имеет активно-емкостный характер.

При частотах выше резонансной сопротивление контура становится активно-индуктивным , причем с дальнейшим ростом частоты φ стремится к 90⁰.

На рис. 7-7,а показано семейство резонансно кривых тока в относительных единицах.

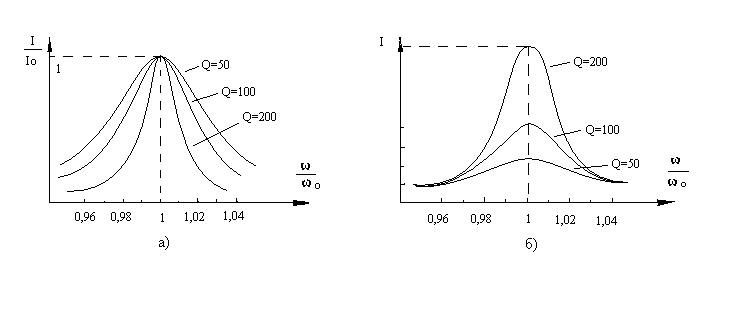
Рис. 7.7 Частотные зависимости тока

Также как и зависимость z/r, кривые I/I₀ для разных Q проходят при резонансе через точку с координатами (I,I)

Если по оси ординат откладывать ток I (вместо отношения I/I₀), то максимумы резонансных кривых тока, построенных для разных значений r, не совпадут в одной точке (рис.7.7,б).

Величина , входящая в выражения (7.II)-(7.I5) может быть названа обобщенной расстройкой контура: она учитывает отклонение частоты от резонансной и добротность Q. Из (7.II) следует, что обобщенная расстройка ξ в случае последовательного контура равна отношению реактивного сопротивления контура к r:

.

Если по оси абсцисс откладывать не относительную частоту ω/ω₀, а обобщенную расстройку ξ, то каждая из зависимостей z/r , I/I₀ и φ вместо семейства кривых представится одной «нормированной кривой» (рис. 7.8).

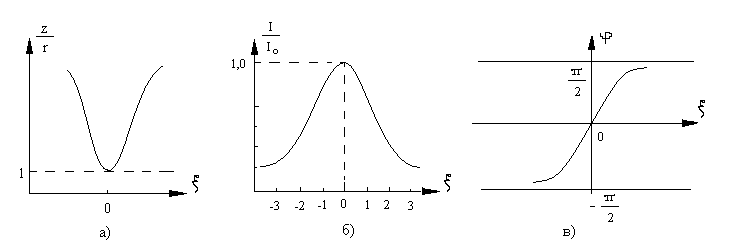
Рис.7.8 Нормированные характеристики сопротивления (а), тока (б) и угла (в)

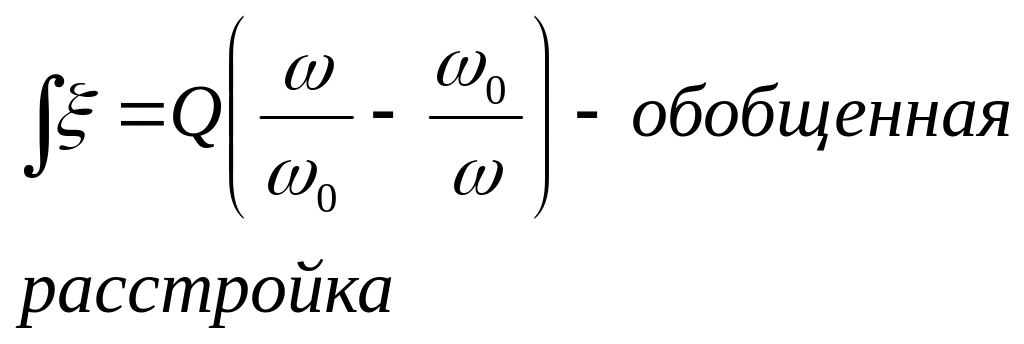
; (7.I7)

Наибольший интерес в частотной характеристике представляет ее часть вблизи точки резонанса. В этой области частот

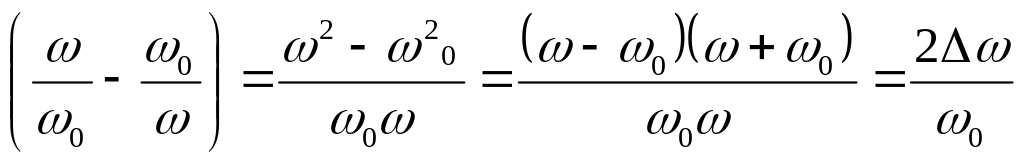, так как вблизи точки резонанса

ω+ω=2 ω₀ (7.I8).

В выражении (7.I8) величина Δω=ω- ω₀ называется расстройкой контура (абсолютной). Она положительна при ω >ω₀ и отрицательна при ω <ω₀ .

Условимся называть относительной расстройкой величину δ=Δω/ω₀. Тогда вблизи точки резонанса

(7.I8)

С учетом (7.I8,a) выражение (7.I2), (7.I3) и (7.I5) упрощается и принимают вид, более удобный для практических расчетов:

; ; (7.I9)

Выражение (7.I9) достаточно точны при δ <0.1. При δ=0,2 погрешность в сопротивлении не менее 10 %.

Чем выше добротность контура Q, тем острее резонансные кривые. Таким образом, величин Q, характеризует остроту резонансной кривой («остроту настройки»), согласно (7.I3), чем больше отношение энергии, запасенной в колебательном контуре к энергии, рассматриваемой в контуре за один период, тем острее резонансная кривая.

Полосу частот вблизи резонанса, на границе которой ток снижается почти до =0.707 максимального (резонансного) значения I₀, принято называть полосой пропускания колебательного контура. При токе I=I₀/ мощность, расходуемая в сопротивлении r , равна:

т.е составляет половину мощности , расходуемой при резонансе. Поэтому полосу пропускания характеризуют, как полосу, границы которой соответствуют половине максимальной мощности. На границах полосы пропускания колебательного контура активное и реактивное сопротивления равны по величине: r=|x| .

Это следует из условия что даёт .

Соответственно и фазовый сдвиг между напряжением на зажимах цепи и током составляет 45⁰: на нижней границе комплексное сопротивление цепи имеет емкостный характер(ток опережает напряжение) и φ=45⁰; на верхней границе комплексное сопротивление цепи имеет индуктивный характер (ток остает от напряжения) и φ=45⁰ .

На основании (7.I7) условие для границы полосы пропускания записывается в следующем виде :

или ξ=_-⁺1. (7.20)

Итак, на границах полосы пропускания обобщенная расстройка по абсолютной величине равна единице. Вблизи резонанса . Поэтому можно записать 2Qδ=I , откуда относительная расстройка частоты на границах полосы пропускания равна и .

Следовательно, при высокой добротности контура полоса пропускания практически симметрична относительно резонансной частоты и находится из условия или . (7.21)

Для контура с невысокой добротностью решение уравнения (7.20) дает:

.

Причем условие (7-21) остается в силе.

Если задана резонансная кривая тока, то для нахождения добротности контура удобно пользоваться формулой

. (7.22)

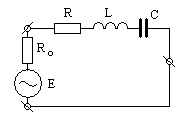
Предыдущие расчетные формулы и частотные характеристики относились к колебательному контуру, питаемому источником э.д.с. E(рис.7.1). Если колебательный контур подключен к источнику напряжения с внутренним сопротивлением r, то последнее, добавляясь к сопротивлению r, влияет на добротность и полосу пропускания контура: чем больше r, тем ниже «эквивалентная добротность»

и тем шире полоса пропускания

Поэтому для получения по возможности более узкой полосы пропускания последовательного колебательного контура выгоден источник напряжения с малым внутренним сопротивлением.