
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
САНКТ-ПЕТЕРБУРГСКАЯ ГОСУДАРСТВЕННАЯ ЛЕСОТЕХНИЧЕСКАЯ АКАДЕМИЯ
Кафедра информатики и информационных систем
РЕШЕНИЕ ЗАДАЧИ АППРОКСИМАЦИИ
с помощью электронной таблицы Excel
Методические указания к выполнению лабораторной и курсовой работы лдя студентов МТД, ЛИФ и ЛМФ и всех форм обучения
г. Санкт-Петербург
2009 г.
Введение
Целью курсовой работы является развитие у студентов навыков обработки экспериментальных данных с помощью электронной таблицы (ЭТ) Excel. На практике достаточно часто возникают задачи приближения функций, полученных в виде таблиц экспериментальных данных. Сами математические методы приближения функций (аппроксимации) изучаются студентами в курсах вычислительной математики и математических методов.
Для решения математических задач существует достаточно большое количество различных математических пакетов, таких как MatLab, MathCad, Math, Mathematica, Mapl и др. Все они охватывают основные разделы математики и позволяют производить подавляющее большинство необходимых математических расчетов. Однако освоение этих пакетов самостоятельно - достаточно трудоёмкая задача. В то же время в курс изучения информатики в большинстве вузов, в том числе и в ЛТА, включено изучение ЭТ Excel. Кроме того, пакет Microsoft Office, в состав которого и входит ЭТ Excel, имеется сегодня практически на каждом компьютере. Конечно, Excel сильно уступает специализированным математическим пакетам, но многие математические задачи аналитической геометрии, линейной алгебры, оптимизации, математического анализа, теории вероятности и статистики, в том числе и аппроксимации могут быть решены с его помощью [1].
Специалист, даже хорошо знающий математику, но не умеющий на практике применять знания, выполнять вычисления с помощью компьютера, едва ли может считаться высококлассным.
Данные методические указания содержат очень краткое описание постановки задачи аппроксимации экспериментальных данных, достаточно подробное описание решения этой задачи на контрольном примере и индивидуальные задания студентам.
Методические указания предназначены для выполнения индивидуальных контрольных работ, курсовых работ, а также могут быть использованы при проведении лабораторных работ студентами всех форм обучения.
1. Постановка задачи аппроксимации
На практике достаточно часто приходится иметь дело с функциями заданными таблично. Предположим, что при изучении функциональной зависимостиy-f(x) двух величин х и у был произведен ряд измерений, результаты которых занесены в таблицу:
![]()
Если аналитическое выражение указанной зависимости неизвестно, то возникает практически важная задача аппроксимации - найти функцию (х), значения которой в известных точках по возможности мало отличалось бы от опытных данных. Функция (х), которая с достаточной точностью определяет зависимость между величинами хиу, называется эмпирической или аналитической.
Таким образом, эмпирическая функция подбирается на основе табличных данных и должна давать удовлетворительное совпадение с этими данными.
Обычно задача аппроксимации распадается на две части. Сначала устанавливают вид зависимости y=f(x), т.е. класс функции к которому должна принадлежать искомая эмпирическая формула, определяют, является ли она линейной, квадратичной, логарифмической или какой-либо другой.
Если нет каких-либо теоретических соображений для подбора вида формулы, обычно строят график табличных данных и сравнивают полученный график с графиками известных функций..
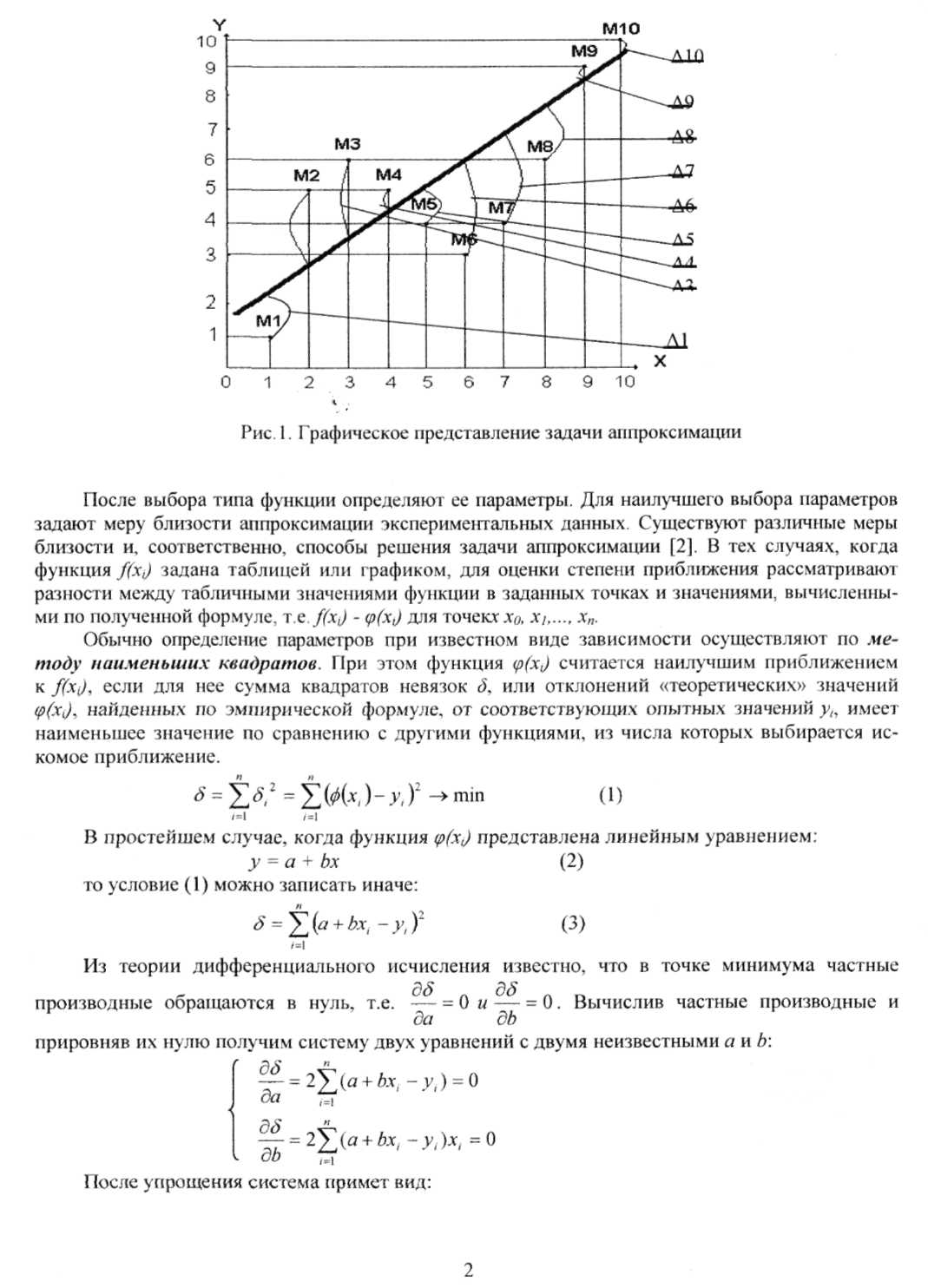
Геометрически смысл задачи аппроксимации состоит в проведении кривой из данного класса (частный случай - прямой), «возможно ближе» примыкающей к совокупности экспериментальных точек Mt(хi,yi), где i=1,2,...,n.
Величина i равная разности между значениями эмпирической функции (х), в точке xt и значением уi, называется уклонением или невязкой (Рис. 1).
Расположение экспериментальных точек на графике может иметь самый различный вид, и каждому соответствует конкретный тип функции
1

3
2. Решение задачи аппроксимации c помощью эт Excel
В Excel задачу аппроксимации можно решать различными способами:
Путём создание таблиц исходных данных и вычисления необходимых сумм (Табл. 1), с последующим вводом в ячейки формул (7, 8) для вычисления коэффициентов, вычисление значений по эмпирической формуле, вычисление отклонений и суммы их квадратов. Этот способ как бы повторяет этапы, которые необходимо было бы выполнить при программировании задачи аппроксимации на любом алгоритмическом языке.
Параметры линейной регрессии можно вычислить с помощью встроенных функций ЛИНЕЙН, НАКЛОН, ОТРЕЗОК
С помощью инструмента для решения оптимизационных задач - Поиск решения. Режим Поиск решения меню Сервис не ориентирован на решение каких-то конкретных задач. Он обладает возможностью изменения и перебора значений указанных элементов при соблюдении широких ограничений, заданных пользователем.
Путем построения их точечного графика с последующим подбором подходящей ап-проксимирующей функции (линии тренда).
Поскольку последний способ аппроксимации с помощью линии тренда является менее трудоёмким и наиболее универсальным, т.к. позволяет проверить шесть вариантов функций и выбрать наиболее адекватную экспериментальным данным, то рассмотрим именно этот способ подбора эмпирической формулы и нахождения её коэффициентов.
