1. Диамагнетики

Магнитный момент молекул диамагнетика равен нулю. Во внешнем магнитном поле у диамагнетика индуцируется (появляется) магнитный момент направленный в противоположную сторону к внешнему полю.

• Магнитная восприимчивость диамагнетика

,

где – средний квадрат расстояния электрона от ядра, n – концентрация атомов, Z – заряд ядра, m – масса электрона.

• Магнитная восприимчивость свободных электронов

,

n – концентрация электронов, μ_Б – магнетон Бора, E_F – энергия Ферми.

2. Парамагнетики

Магнитный момент парамагнетика в отсутствии внешнего поля не равен нулю. Магнитные моменты молекул в отсутствии внешнего поля ориентированы равновероятно.

Закон Кюри. Магнитная восприимчивость обратно пропорциональна температуре.

.

где μ - магнитный момент атома (молекулы), μ₀ - магнитная постоянная, k - постоянная Больцмана, T - абсолютная температура, N – число неспаренных электронов в единице объема.

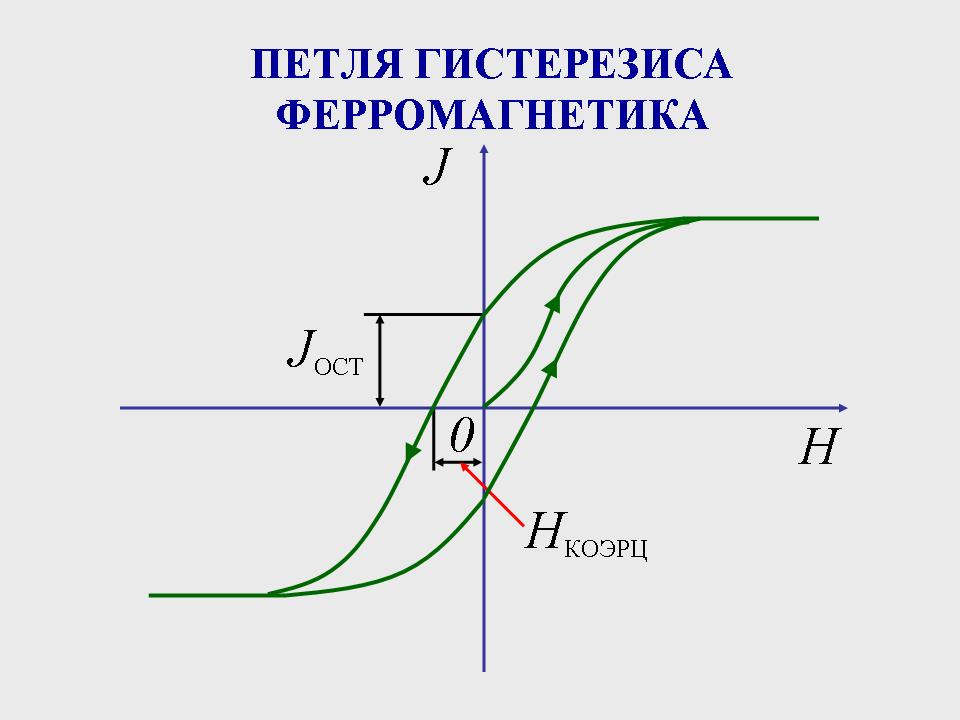
10. Ферромагнетики.

В отсутствие внешнего поля атомы ферромагнетиков имеют очень большой магнитный момент. Данная группа магнетиков обладает спонтанной (самопроизвольной) намагниченностью в отсутствии внешнего поля.

1. Магнитная проницаемость ферромагнетиков достигает нескольких тысяч единиц.

2. З ависимость J от H нелинейная, следовательно, намагниченность зависит от напряженности внешнего поля.

3. При изменениях поля значения намагниченности отстают от напряженности поля H, в результате чего J и B определяются не только величиной H в данный момент времени, но и предшествующими значениями H (зависит от предыстории магнетика). Это явление называется гистерезисом. При циклических изменениях поля формируется петля гистерезиса.

4. Остаточная намагниченность (J_ост) возникает после того, как ферромагнетик находился в магнитном поле.

5. Коэрцитивная сила (Н_клерц) – это то значение напряженности, при котором намагниченность становится равной нулю.

6. Ферромагнетик разбивается на домены в пределах которых он самопроизвольно (спонтанно) намагничен до насыщения.

7. Температура, при которой ферромагнетик утрачивает необычные свойства, превращаясь в парамагнетик, называется точкой Кюри.

13. Закон Кюри-Вейсса

,

где g – фактор Ланде, определяет связь между магнитным и полным моментом системы, S – полный момент системы, Θ - температура Кюри, N – число неспаренных электронов в единице объема.

14. При переходе через границу раздела двух сред с разными магнитными проницаемостями, а также через границу магнетика с вакуумом нормальная составляющая вектора и тангенциальная составляющая вектора не изменяются

, .

15. Тангенциальная составляющая индукции и нормальная составляющая напряженности скачкообразно изменяются (терпят разрыв)

, .

Законы постоянного тока.

Определения

• Участок цепи называется однородным, если на нем действуют только электростатические силы (отсутствует ЭДС).

• Участок цепи называется неоднородным, если на нем действуют как сторонние, так и электростатические (в цепь включена ЭДС).

• Цепь называется замкнутой, если в ней действуют только сторонние силы (разность потенциалов равна нулю).

• Электрическое сопротивление (R,r) – скалярная величина, характеризующая способность проводника препятствовать переносу электрического заряда.

,

где ρ - удельное сопротивление материала проводника, l –длина проводника, S – площадь поперечного сечения проводника.

• Удельная проводимость проводника

.

1. Разность потенциалов (φ₁–φ₂) равна работе электростатических сил по перемещению единичного положительного заряда.

,

где q₊ - единичный положительный заряд

2. Электродвижущая сила (ε) равна работе сторонних сил по перемещению единичного положительного заряда.

3. Падение напряжения (U) равно работе электростатических и сторонних сил по перемещению единичного положительного заряда.

4. Сила тока

5. Плотность тока

,

где - единичный вектор направления движения носителей тока в данной точке проводника.

6. Связь плотности тока со средней скоростью направленного движения носителей тока

,

где q - заряд носителя тока, n - концентрация носителей.

7. Падение напряжения

,

здесь U – падение напряжения на участке цепи, φ₁ - потенциал начала участка, φ₂ -потенциал в конце участка, ε - электродвижущая сила источника тока.

Для однородного участка цепи падение напряжения равно разности потенциалов

.

8. Закон Ома (интегральная форма)

где I – сила тока в цепи, U – падение напряжения на участке цепи, R – электрическое сопротивление внешней цепи, r – внутренне сопротивление источника тока.

9. Закон Ома для однородного участка цепи

.

10. Закон Ома для замкнутой цепи

.

11. Правила Кирхгофа:

• первое – алгебраическая сумма токов в узле равна нулю

.

Втекающий в узел ток положительный, вытекающий отрицательный.

• второе – алгебраическая сумма падений напряжения в контуре равна алгебраической сумме ЭДС в контуре.

.

• Падение напряжения положительное, если направление обхода по контуру совпадает с направлением тока.

• ЭДС положительная, если при обходе по контуру подходим к ЭДС со стороны отрицательной клеммы.

12. Работа электрического тока

,

A_I – работа, совершаемая током за время t.

13. Закон Джоуля-Ленца (интегральная форма)

,

Q – количество теплоты выделившейся в проводнике за время t.

14. Мощность тока (интегральная форма)

.

15. Закон Ома (дифференциальная форма) для однородного участка цепи

,

- плотность тока, - удельная проводимость (величина обратная удельному сопротивлению ρ), - напряженность электрического поля в проводнике.

16. Связь удельной проводимости с подвижностью положительных и отрицательных носителей

,

где b⁺ и b^– соответственно подвижность положительных и отрицательных носителей тока.

17. Закон Ома (дифференциальная форма) для неоднородного участка цепи

,

где - напряженность сторонних сил.

18. Закон Джоуля-Ленца (дифференциальная форма)

,

где Q_удель - количество теплоты, выделившееся в единице объема в единицу времени, ρ - удельное сопротивление.

19. Удельная тепловая мощность

.

20. Классическое выражение для удельной проводимости

,

где n – концентрация носителей, е - элементарный заряд (или заряд носителя тока), τ -средне время свободного пробега электрона (носителя тока), m - масса электрона (носителя тока).