Законы сохранения в механике.

1. Закон сохранения импульса системы тел (система тел замкнутая)

.

2. Закон сохранения момента импульса системы тел (система тел замкнутая)

.

3. Закон сохранения механической энергии (система тел консервативная, изолированная)

,

где - кинетическая энергия, - потенциальная энергия.

Элементы специальной теории относительности.

Постулаты:

1. Обобщенный принцип относительности.

2. Постоянства скорости света.

Скорость света в вакууме с=3·10⁸ м/с.

Преобразования Лоренца.

Система К' движется в положительном направлении оси ОХ со скоростью v.

Преобразование скорости

Лоренцево сокращение длины, площади, объема и плотности

Линейные размеры уменьшаются в направлении движения

Длина предмета:

l – длина движущегося стержня, l₀ длина покоящегося стержня.

Площадь:

S – площадь движущейся плоской фигуры, S₀ – площадь покоящейся плоской фигуры.

Объем:

V – объем движущегося тела, V₀ – объем покоящегося тела.

Плотность вещества: .

ρ - плотность движущегося тела, ρ₀ -плотность покоящегося тела.

Лоренцево сокращение временного интервала

,

где Δt – время между двумя событиями, происходящими на движущемся объекте, Δt' – время между двумя событиями, происходящими на покоящемся объекте.

Пространственно-временной интервал (инвариант)

Масса движущегося тела

,

где m – масса движущегося тела, m₀ – масса покоящегося тела.

Импульс тела

.

Энергия движущегося тела

.

Энергия покоящегося тела

.

Кинетическая энергия тела

.

Дефект массы

.

Средняя энергия молекул.

1. Основное уравнение МКТ для давления записанного через энергию хаотического движения молекулы

,

где - средняя кинетическая энергия поступательного движения одной молекулы.

2. Средняя кинетическая энергия поступательного движения одноатомной молекулы:

,

где k - постоянная Больцмана, T - абсолютная температура.

3. Средняя полная кинетическая энергия одной молекулы

,

где i - число степеней свободы молекулы (i=i_П+i_B+2i_K):

-одноатомная молекула i=i_П= 3;

-двухатомная i=i_П + i_B = 3 +2 = 5;

-трехатомная и более i=i_П + i_B = 3 +3 = 6;

-двухатомная с упругой связью i=i_П + i_B +2i_K= 3 +2 + 2 = 7;

Колебательная степень свободы эквивалентна двум поступательным или вращательным степеням свободы.

Распределения Максвелла и Больцмана.

Р аспределение Максвелла по скоростям

,

m₀ - масса молекулы, v - скорость молекулы, k – постоянная Больцмана, Т – абсолютная температура.

Вероятнейшая скорость

,

R – универсальная газовая постоянная, μ - молярная масса.

Средняя скорость

.

Средняя квадратическая скорость

.

Максимальное значение функции Максвелла

.

Распределение по энергиям

.

где ε – кинетическая энергия поступательного движения молекулы.

Распределение Больцмана

1. Барометрическая формула

,

где р – давление на высоте h, р₀ – давление на нулевой высоте, μ – молярная масса, h – высота, R – универсальная газовая постоянная, k постоянная Больцмана, Т – абсолютная температура.

2. Для концентрации частиц

,

г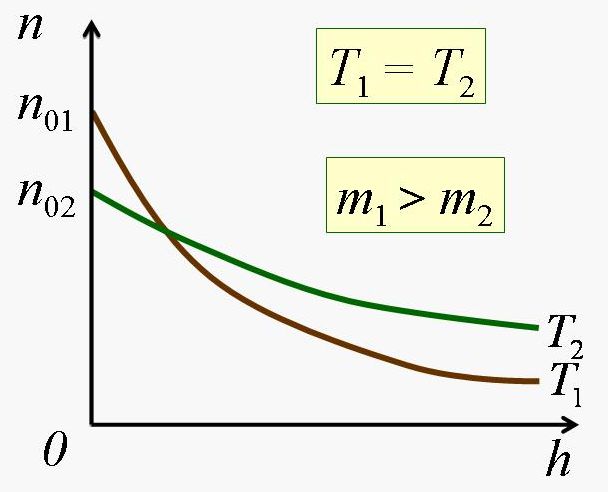 де n – концентрация молекул на высоте h, n₀ – концентрация молекул на нулевой высоте. Остальные обозначения прежние.

3. Распределение Больцмана

,

где n – концентрация молекул в том месте, где потенциальная энергия молекул равна Е_р, n₀ – концентрация молекул в том месте, где потенциальная энергия молекул равна нулю (Е_р=0). Остальные обозначения прежние.