Примеры.

1. , эллиптический тип.

Уравнение характеристик

2. , параболический тип.

(любая)

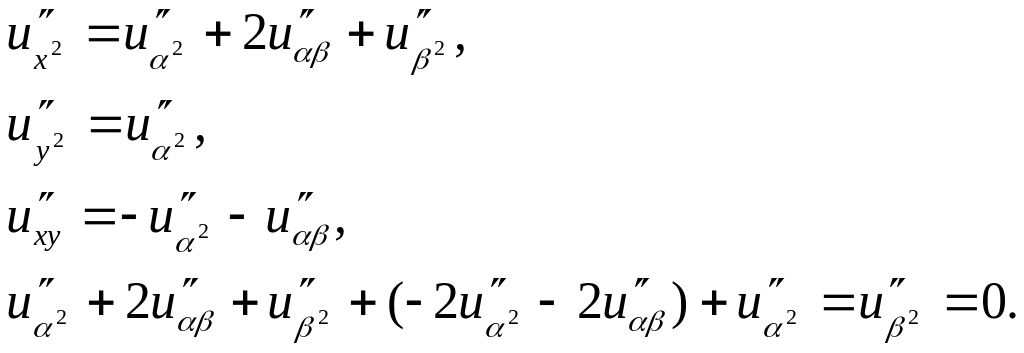
3. , гиперболический тип.

Уравнение характеристик

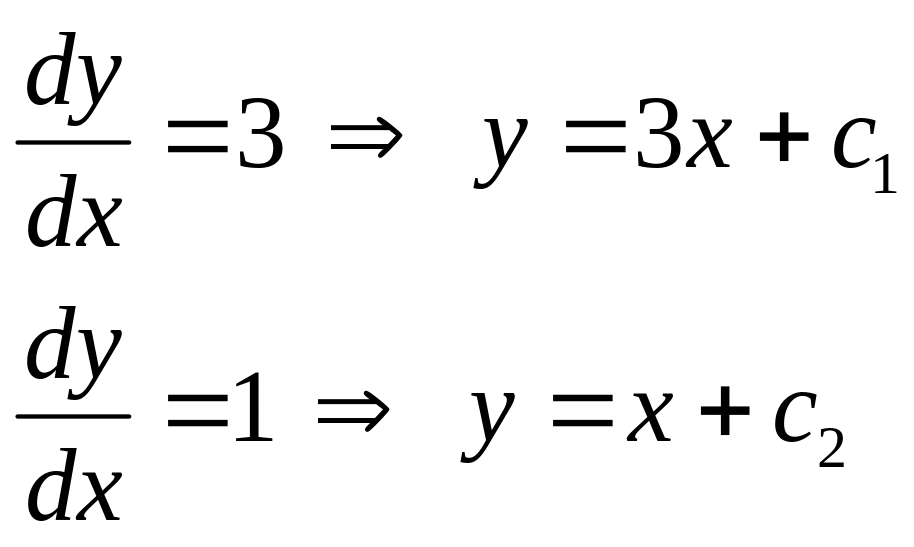
Тема 3. Классификация краевых задач.

Лекция 1. Классификация краевых задач.

Рассматриваемые вопросы.

1.Типы краевых задач.

2. Краевая хадача для уравнений эллиптического типа.

3. Задачи Дирихле и Неймана.

Из курса обыкновенных дифференциальных уравнений известно, что решение дифференциального уравнения n-го порядка

(1)

определяется неоднозначно. Общее решение зависит от n произвольных постоянных и для однозначной разрешимости необходимо задать так называемые начальные условия

(2)

Решение задачи для уравнения (1) с начальными условиями (2) называется задачей Коши и при определенных условиях решение этой задачи существует и единственно.

Более сложная ситуация складывается при рассмотрении дифференциальных уравнений в частных производных. В самом деле: общим решением простейшего уравнения является произвольная функция

Для того, чтобы сделать решение определенным, нужно задать дополнительные условия, например, потребовать чтобы неизвестная функция, а возможно и ее производные принимали заданные значения на некоторых многообразиях. Каждая задача математической физики ставится как задача об отыскании решения некоторого уравнения при определенных дополнительных условиях, которые в большинстве случаев диктуются ее физической постановкой.

В задаче о колебании струны нужно искать решение уравнения

(3)

при условиях

а) струна закреплена

– однородные граничные условия (4)

б) концы не закреплены

– неоднородные граничные условия (4’)

Кроме того, необходимо знать начальное положение струны и начальный импульс

– начальные условия (5)

Условия (4) или (4’) совместно с условиями (5) полностью определяют решение дифференциального уравнения (3) и потому среди них нет лишних.

Аналогично, если рассматривать задачу о колебании мембраны, занимающей плоское положение ω с границей S, то решение этой задачи сводится к решению уравнения:

при дополнительных условиях:

– начальные условия

и

– граничное условие.

Иногда вместо на S задается линейная комбинация

– граничное условие.

Задачу с заданными граничными и начальными условиями называют смешанной задачей. Аналогично может быть поставлена задача для уравнения теплопроводности: пусть – температура тела в момент времени t. Тогда

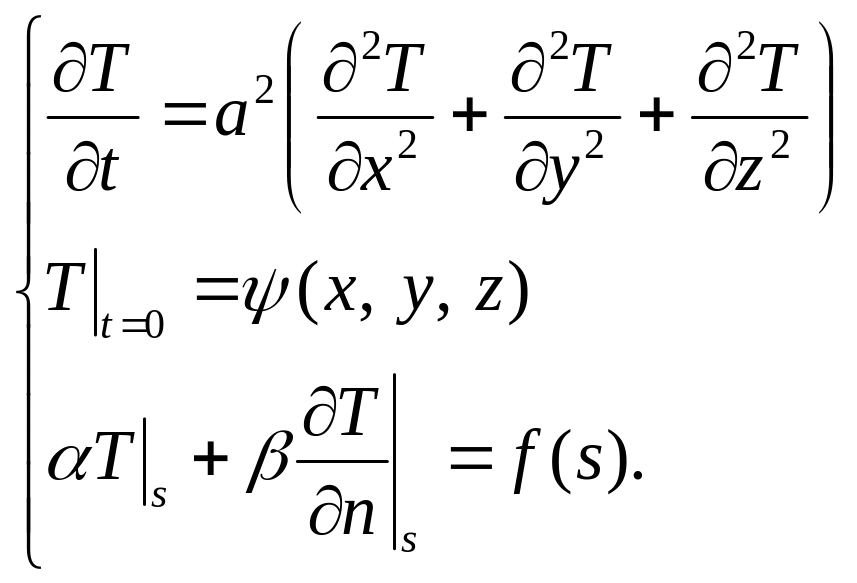
Если же рассматривать установившейся тепловой режим, тогда и

(6)

Решение этого уравнения можно искать при условии

Особый интерес представляют случаи, когда α=0 или β=0.

α=0 – задача Дирихле

β=0 –задача Неймана

Уравнение (6) не обязательно решать лишь в конечной области. Очень часто бывает важно решить его для области неограниченной. Это бывает, когда размеры рассматриваемой области очень велики по сравнению с масштабом изучаемого явления.

Например, при изучении явления теплоотдачи некоторого длинного трубопровода, заложенного в земле, считать, что земля не шар, а неограниченное полупространство. При рассмотрении неограниченных областей далеко не безразлично, как ведет себя решение в далеких точках изучаемой области.

Во многих случаях задача становится определенной только при известных предположениях об этом поведении (например, решение при .

2. Понятие о задаче, поставленной корректно. Пример Адамара.

Задача с начальными условиями называется поставленной корректно, если ее решение «непрерывно» зависит от этих начальных данных. Для дифференциальных уравнений в частных производных это не всегда так. Рассмотрим пример, принадлежащий Адамару.

Найдем решение уравнения в полуплоскости удовлетворяющее условиям

Легко проверить, что решение это будет иметь вид

(7)

Можно показать, что такое решение единственно.

Функция равномерно и не только она сама, но и все ее производные.

Однако решение (7) при любом имеет вид косинусоиды с как угодно большой амплитудой и не стремится к какому-либо пределу. При х=0 оно просто неограниченно растет. Задача поставлена некорректно.