Лабораторные в Excel по статистике / st_4

Статистика

Цель работы. Решение задач множественной регрессии с помощью Excel.

Задание. Выберите переменные и опишите регрессионной зависимостью пробег на одном галлоне топлива в следующей задаче.

В файле 4.xls содержатся данные о 106 моделях автомобилей выпущенных в 2000 году. Обозначения: Drive Type(Front, Rear) – тип автомобиля (переднеприводной, заднеприводной); Mileage(mpg) – пробег на одном галлоне топлива (миль на галлон); Fuel Type (Regular, Premium) - тип топлива (обычное, улучшенное); Capacity (gal) - объем топливного бака (галлонов); Length (inches) - длина (дюймы); Wheel Base – колесная база; Width – ширина; Door Top – высота двери; Luggage – объем багажника; Front Shoulder - место для плечей спереди; Front Leg Room - место для ног спереди; Front Head Room - место для головы спереди; Rear Shoulder - место для плечей сзади; Rear Leg Room - место для ног сзади; Rear Head Room - место для головы сзади.

Порядок выполнения работы

1. Перейдите к фиктивным переменным для качественных значений исходных данных. Предварительно скопируйте исходные данные на новый лист.

2. Вычислите корреляционную матрицу. Для удобства вычислений целесообразно столбец со значениями функции расположить перед столбцами аргументов

3. Выберите в первой строке корреляционной матрицы не более трех аргументов, имеющих наибольшие значения коэффициентов корреляции со значениями функции и наименьшие значения коэффициентов взаимной корреляции.

4. Составьте с выбранным набором аргументов все возможные уравнения регрессии (три - с одним аргументом, три - с двумя аргументами и одно с тремя аргументами).

5. Выберите лучшие модели по критерию максимума коэффициента детерминации.

6. Для лучших моделей рассчитайте среднее значение коэффициента вариации.

7. Повторите п.4 для лучших моделей еще раз, использовав только 80% исходных данных.

8. Рассчитайте сумму квадратов остатков на проверочной последовательности по оставшимся 20% исходных данных.

9. Вычислите коэффициент корреляции для лучших моделей и интерпретируйте его. Сравните два способа вычисления коэффициента корреляции: 1) как квадратный корень из коэффициента детерминации; 2) как коэффициент корреляции между и.

10. Сформулируйте нулевую гипотезу и проверьте значимость уравнения в целом на уровне 0,05 с помощью - теста (распределение Фишера). вычислите с помощью встроенной функции FРАСПОБР(). Число степеней свободы 1 равно числу коэффициентов в уравнении регрессии, число степеней свободы 2 равно числу наблюдений без единицы, уменьшенному на число степеней свободы 1.

11. Выберите лучшую модель на основании сравнения коэффициентов детерминации, среднего значения коэффициента вариации, суммы квадратов остатков на проверочной последовательности и значения 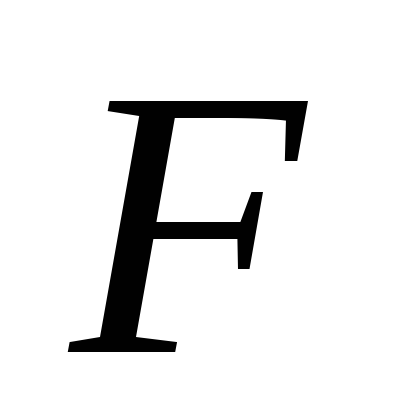- теста. Обоснуйте свой выбор.

Лабораторная работа №4