Вогнутость и выпуклость графика функции

График дифференцируемой функции называется вогнутым в промежутке если соответствующая часть кривой расположена выше всех касательных, проведенных в любых ее точках.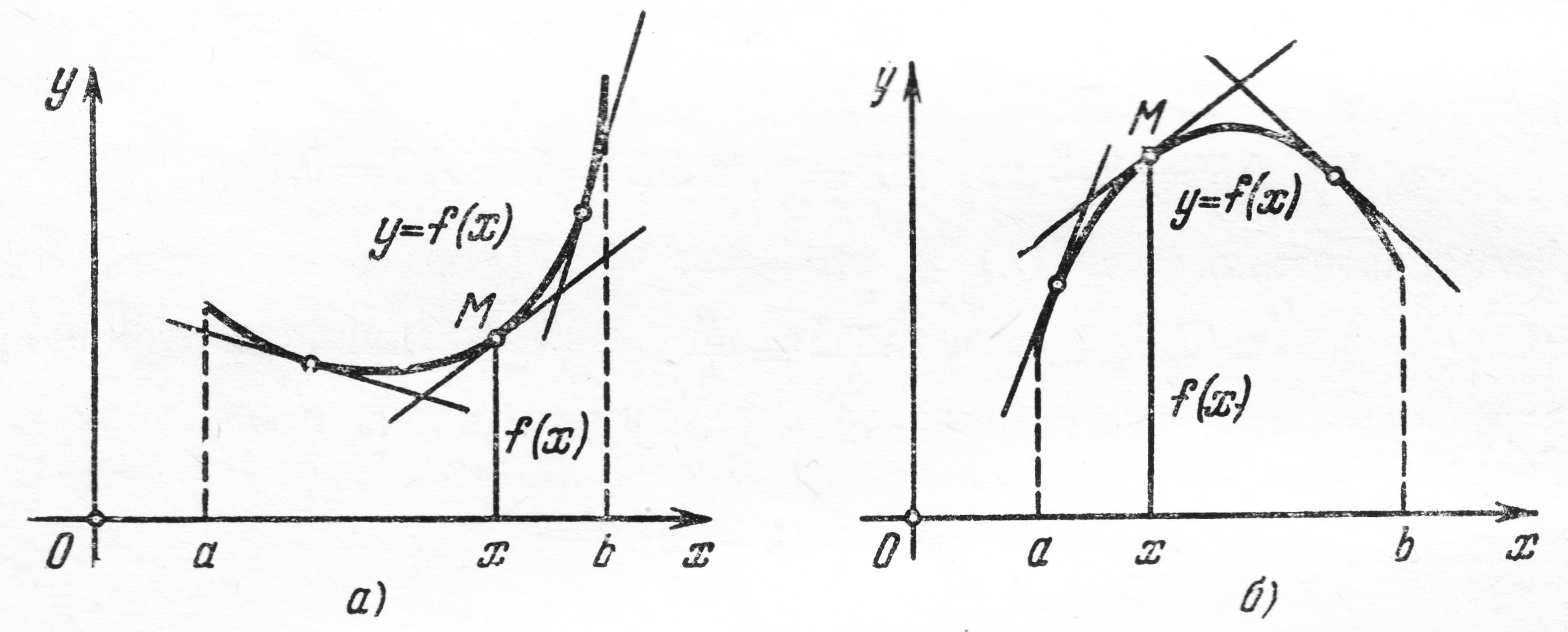

График дифференцируемой функции называется выпуклым в промежутке если соответствующая часть кривой расположена ниже всех касательных, проведенных в любых ее точках.

Теорема о необходимом условии выпуклости (вогнутости) графика функции

1) Если графиком дважды дифференцируемой функции на является выпуклая кривая, то на

2) Если графиком дважды дифференцируемой функции на является вогнутая кривая, то на

Доказательство. 1) Примем за функцию а за ее производную Так как кривая на выпукла, то на убывает, а необходимым условием ее убывания мы уже знаем является то, что ее производная на Что и требовалось доказать.

2)Аналогично доказывается вторая часть теоремы.

Теорема о достаточном условии вогнутости (выпуклости) графика функции

1) Если для дважды дифференцируемой функции то график этой функции будет вогнутым в данном промежутке.

2) Если же то график функции будет выпуклым в этом промежутке.

Доказательство. 1) Пусть и - любая точка Сравним в точке ординату кривой с ординатой ее касательной проведенной в точке Так как угловой коэффициент касательной равен то Отсюда Используя теорему Лагранжа, будем иметь где - точка, лежащая между Поэтому

Так как то - возрастающая функция.

Пусть ; тогда и в силу возрастания имеем В этом случае получаем

Если теперь то Снова

Таким образом, при имеем т.е.

Отсюда вытекает, что при кривая расположена выше своих касательных и, значит, график функции будет вогнутым на

2) Аналогично доказывается, что если при то график функции будет выпуклым на

З десь снова действует правило дождя .

Пример. Установить интервалы выпуклости и вогнутости.

, следовательно, при кривая выпукла, а при - вогнута.

Т очки перегиба

Точкой перегиба графика дифференцируемой функции называется его точка, при переходе через которую кривая меняет свою вогнутость на выпуклость или наоборот.

Теорема о необходимом признаке точки перегиба

Если - абсцисса точки перегиба графика дифференцируемой функции то либо либо не существует.

Доказательство. Мы определили точку перегиба, как такую точку графика, которая отделяет выпуклую часть непрерывной кривой от вогнутой. Из доказанной выше теоремы о необходимом условии вогнутости (выпуклости) графика функции следует, что с одной стороны от точки а с другой таким образом, точка разделяет два интервала монотонности функции следовательно, она является точкой экстремума для функции Применяя теорему о необходимом условии экстремума функции, получаем, что если – абсцисса точки перегиба, то либо равняется нулю, либо не существует.

Те точки в которых или не существует, называются критическими точками второго рода для функции Критическая точка второго рода не обязательно должна быть абсциссой точки перегиба, но только среди критических точек второго рода надо искать абсциссы точек перегиба.