Предел функции нескольких переменных

Будем в основном рассматривать функции двух переменных, так как рассмотрение трех и более переменных не вносит никаких принципиальных изменений, но вносит добавочные технические трудности.

Введем одно очень важное вспомогательное понятие – понятие окрестности данной точки.

Окрестностью радиуса точки 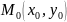называется множество всех точек удовлетворяющих неравенству 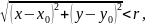т.е. множество всех точек, лежащих внутри круга радиуса с центром в точке

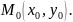
Если мы будем говорить, что функция 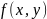обладает каким-либо свойством вблизи точки 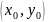или в окрестности точки 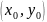то под этим будем подразумевать, что найдется такой круг с центром в 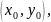во всех точках которого данная функция обладает указанным свойством.

П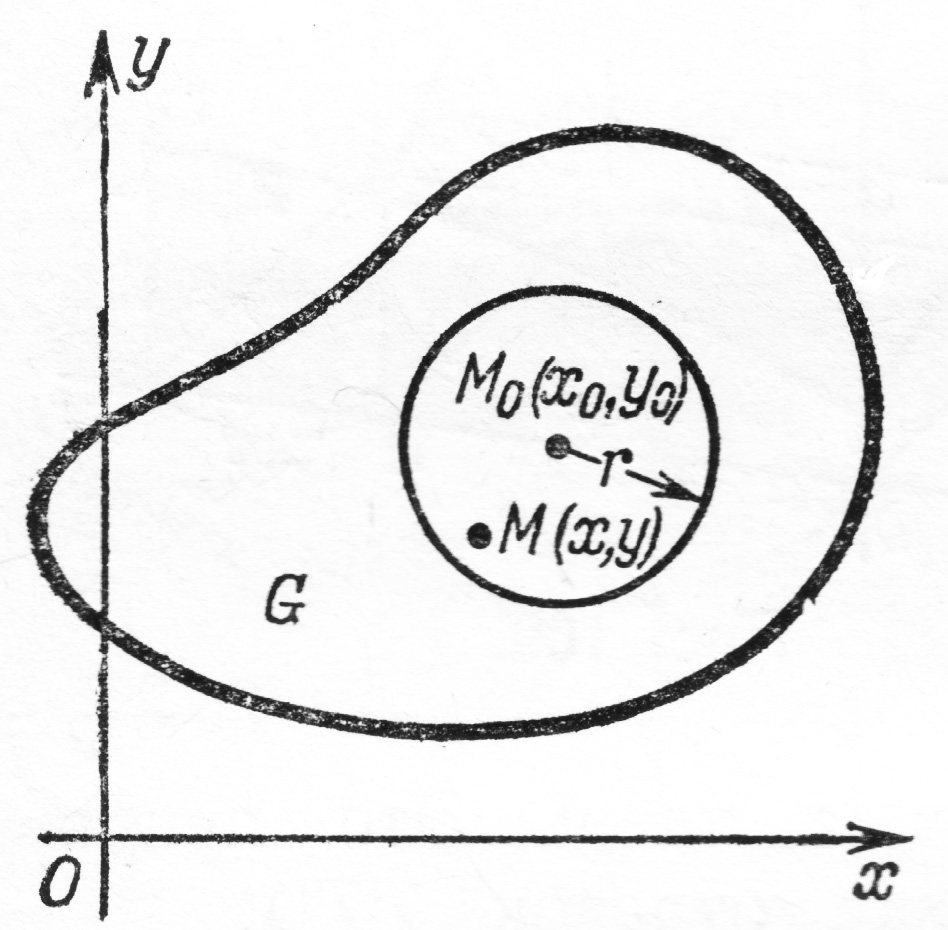 усть дана функция определенная в некоторой области плоскости Рассмотрим некоторую определенную точку лежащую в области

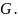
Число называется пределом функции при стремлении точки к точке если такое 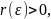что для всех точек для которых выполняется неравенство 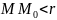имеет место неравенство

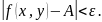
Если число является пределом функции при

то пишут:

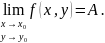
Функция 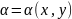называется бесконечно малой при

если

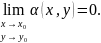
Как и для функции одной переменной, существует специальное представление функции двух переменных:

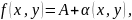
где

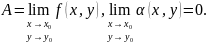
Рассуждая как и в случае функции одной переменной, можно доказать также теорему о пределе суммы, разности, произведения и частного функций нескольких переменных, аналогичную соответствующей теореме для функции одной переменной.

Лекция 24.

Непрерывность функции нескольких переменных

Функция называется непрерывной в точке если она

1) определена в точке 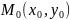и в некоторой ее окрестности,

2) существует предел

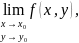
3) этот предел равен частному значению

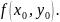
Условие непрерывности функции в точке символически может быть выражено так:

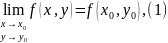
причем точка стремится к точке произвольным образом, оставаясь в области определения функции.

Если обозначим то равенство можно переписать так:

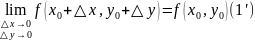
или

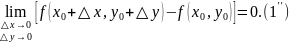
Обозначим

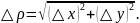
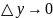
При и 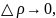и обратно,

если то и

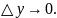
Замечая далее, что выражение, стоящее в квадратных скобках в равенстве 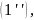есть полное приращение функции равенство можно переписать в форме:

Это условие непрерывности функции в точке в разностной форме.

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области.

Теорема. Если функция определена и непрерывна в замкнутой области, то она ограничена и достигает своего наименьшего и наибольшего значений (без доказательства).

Если в некоторой точке не выполняется хотя бы одно из трех условий непрерывности функции в точке, то точка называется точкой разрыва функции

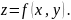
Функция двух переменных может иметь не только точки разрыва, но и линии разрыва. Например, для функции 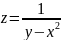любая точка параболы является точкой разрыва. Говорят, что данная функция имеет линию разрыва.

Аналогично, говорят, что функция трех переменных 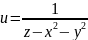имеет поверхность разрыва – параболоид вращения