Интегрирование по частям
Пусть
и
дифференцируемые функции от
Тогда
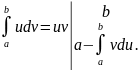
Последняя формула называется формулой интегрирования по частям.
Пример.
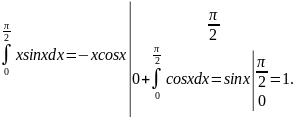
Приближенное вычисление определенных интегралов
1. Формулы прямоугольников.
Пусть на отрезке
задана непрерывная функция
Требуется вычислить определенный
интеграл
Разделим отрезок
точками
на
равных частей длины
Обозначим далее
через
значения функции
в точках
т.е.
Составим суммы:
Каждая из этих сумм является интегральной суммой для на и поэтому приближенно выражает интеграл:
Это и есть формулы прямоугольников.
И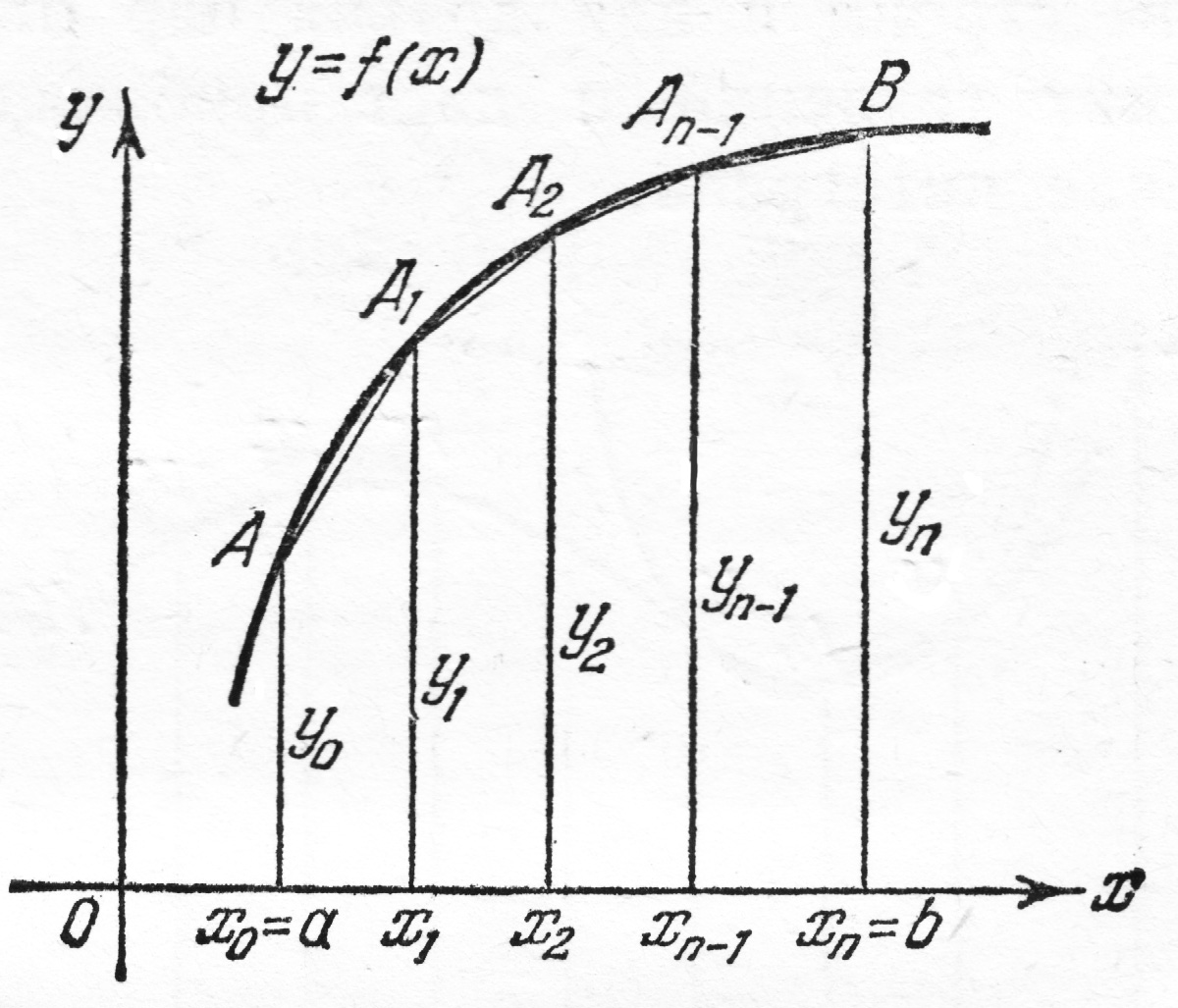
з
рисунка ясно, что если
положительная и возрастающая функция,
то (1) выражает площадь ступенчатой
фигуры, составленной из
входящих
прямоугольников, а (1') – площадь
ступенчатой фигуры, составленной из
выходящих
прямоугольников.
Ошибка
тем меньше, чем больше
(меньше шаг деления
2. Формула трапеций.
Естественно
ожидать, что мы получим более точное
значение определенного интеграла, если
данную кривую
заменим не ступенчатой линией, как это
было в формулах прямоугольников, а
вписанной ломаной. Тогда площадь
криволинейной трапеции
заменится суммой площадей прямолинейных
трапеций, ограниченных сверху хордами
Так как площадь первой из этих трапеций
равна
второй -
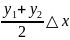и т.д., то
или
Это и есть формула трапеций.
Число, стоящее в правой части формулы (2), есть среднее арифметическое чисел, стоящих в правых частях формул (1) и (1').
Чем больше будет
(меньше шаг деления
тем с большей точностью сумма, написанная
в правой части приближенного равенства
(2), будет давать значение интеграла.
Лекция 17.
Приложения определенного интеграла Площадь криволинейной фигуры в прямоугольных координатах
Как было показано
ранее, площадь криволинейной трапеции
вычисляется по формуле:
Здесь предполагалось,
что
и
Е
сли
же будет
но
то
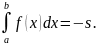
Площадь криволинейной
трапеции
определяется формулой:
Площадь
криволинейной фигуры
вычисляется
по формуле:
Эта формула получается с помощью формулы (1), т.к. указанная фигура представляет разность двух криволинейных трапеций.
П
лощадь
фигуры
определяется формулой:
В более общем случае криволинейную фигуру разбивают на части, площади которых вычисляются по приведенным формулам или определяются непосредственно.
Если
и
меняет знак на отрезке
то определенный интеграл равен
алгебраической сумме площадей
соответствующих криволинейных трапеций:
П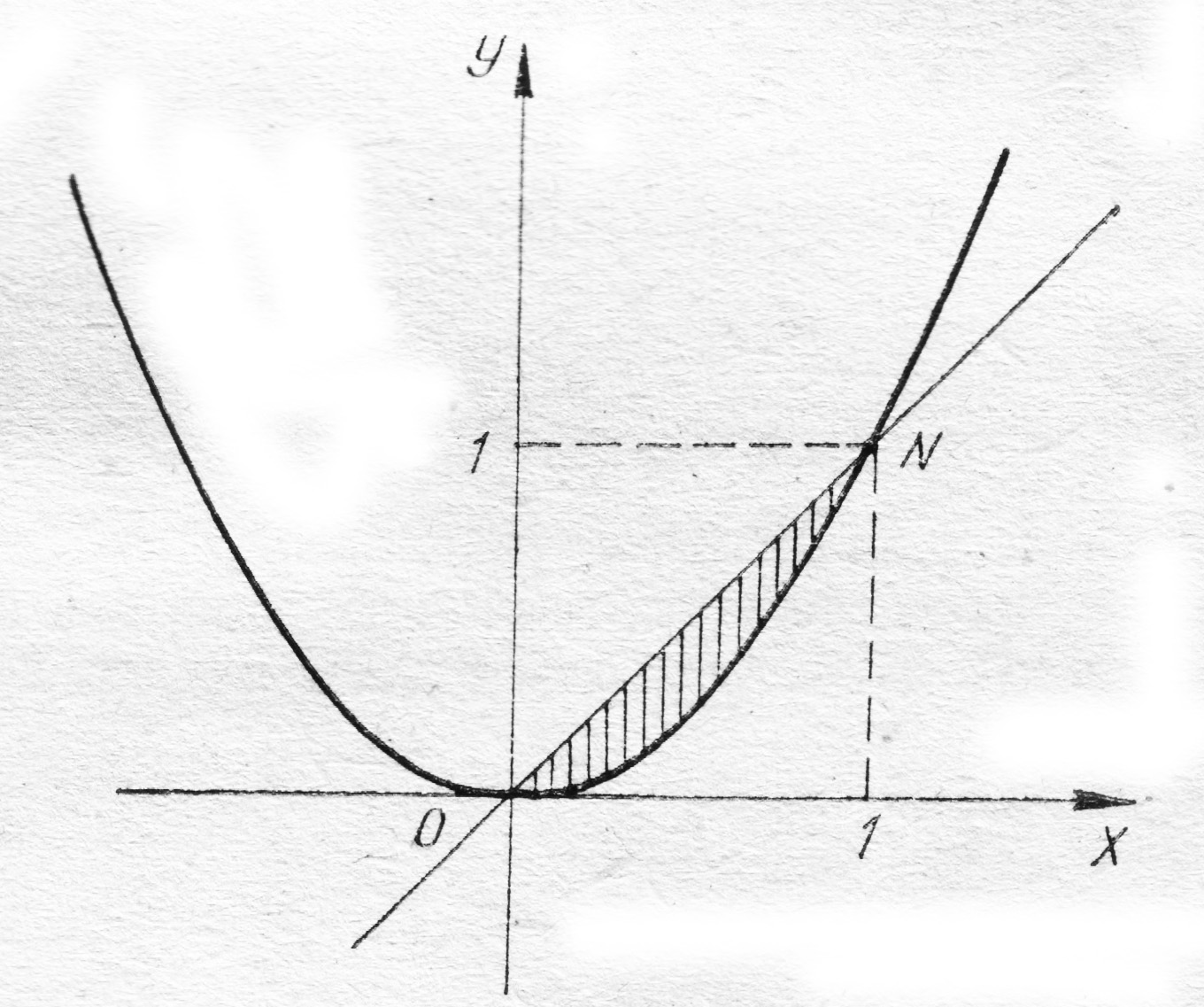
ример.
Вычислить площадь криволинейной фигуры,
ограниченной параболой
и прямой
Данные линии пересекаются в точках
и
Воспользуемся формулой (3):
Рассмотрим случай, когда линия, ограничивающая криволинейную трапецию сверху, задана параметрическими уравнениями:
где
Уравнения (5) определяют некоторую функцию на отрезке Площадь криволинейной трапеции вычисляется по формуле:
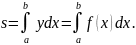
Перейдем к новой
переменной по формуле
тогда
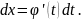На основании
уравнений (5) получаем:
С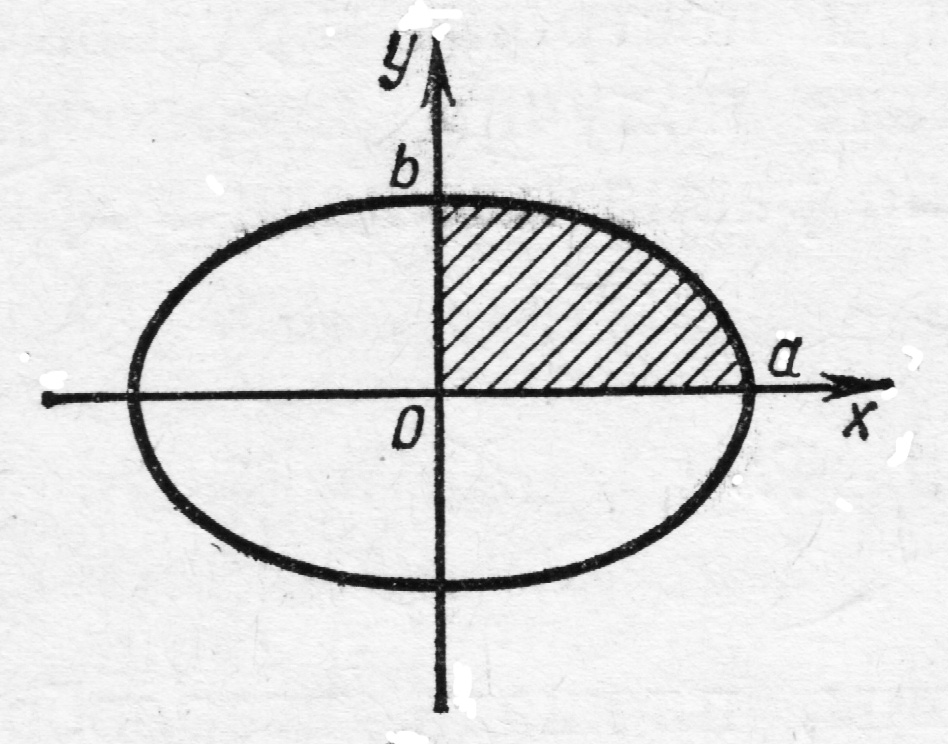
ледовательно:
Пример. Вычислить площадь области, ограниченной эллипсом:
В силу симметрии эллипса относительно координатных осей достаточно вычисπлить площадь области, лежащей в первой четверти, и результат умножить на 4. Находим новые пределы:
|
|
|
t |
|
|
В частном случае,
когда
получим
площадь круга радиуса
