Интегрирование некоторых классов тригонометрических функций Интеграл вида
Этот интеграл
с помощью подстановки
всегда сводится к интегралу от рациональной функции.
Далее,
Таким образом,
и
выразились
рационально через
Подставляя полученные выражения в
получим интеграл от рациональной
функции.
Пример.
Рассмотренная
подстановка дает возможность
проинтегрировать всякую функцию вида
Поэтому ее называют
универсальной
тригономнтрической подстановкой
Однако, на практике она часто приводит
к слишком сложным рациональным функциям.
Поэтому наряду с
универсальной
подстановкой бывает полезно знать
также другие подстановки, которые в
некоторых случаях быстрее приводят к
цели.
1) Если интеграл
имеет вид
то подстановка
приводит этот интеграл к виду
2) Если интеграл
имеет вид
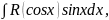то подстановка
приводит его к виду
3) Если интеграл
имеет вид
то подстановка
приводит его к виду
4) Если интеграл
имеет вид
но
и
входят только в четных степенях, то
применяется подстановка
т.к.
и
выражаются рационально через
После подстановки получим интеграл от
рациональной функции.
5) Пусть интеграл
имеет вид
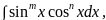где
и
целые
числа. Рассмотрим три случая.
и
таковы, что по крайней мере одно из них
нечетное число. Допустим для определенности,
что
нечетное. Положим
Сделаем замену
и
числа неотрицательные и четные.
Положим
,
Возводя в степень
и раскрывая скобки, получим члены,
содержащие
в нечетных и четных степенях. Члены с
нечетными степенями интегрируются ,
как указано в случае
Четные показатели степеней снова
понижаем по формулам
Продолжая так, дойдем до членов вида
которые легко интегрируются.
и
числа
четные, причем хотя бы одно из них
отрицательно.
В этом случае
предыдущий прием не проходит и приходится
поступать как в пункте 4), т.е. делать
подстановку
или
6) Рассмотрим
интегралы вида:
Они берутся при
помощи следующих формул
Подставляя и интегрируя, получим
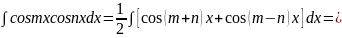
Аналогично вычисляются и два других интеграла.
Интеграл вида (тригонометрические подстановки)
Предполагается,
что
и
Покажем метод преобразования этого интеграла к интегралу вида
который был рассмотрен нами.
Сделаем замену:
Тогда
Рассмотрим все возможные случаи.
1. Пусть
Введем обозначения
2. Пусть
Тогда
3. Пусть
Тогда
4. Пусть
В этом случае
есть комплексное число при любом
значении
Таким образом, интеграл (1) преобразуется к одному из следующих типов.
Интеграл I
типа приводится к интегралу вида (2) с
помощью подстановки
Для интеграла II
типа нужно применить подстановку
А в интеграле III
типа следует сделать подстановку
Пример.
Это интеграл III
типа. Делаем подстановку
