4. Астрономические и геодезические координаты.

Уклонения отвесных линий.

4.1. Астрономические и геодезические координаты.

Положение точки на поверхности Земли определяется ее географическими координатами: широтой и долготой.

Географические координаты могут быть астрономическими и геодезическими. Они показывают положение любой точки на поверхности земного эллипсоида или на геоиде. Геодезические координаты определяются геодезическими методами сложным путем, но очень точно (с ошибкой 0,001÷0,0001″). Астрономические координаты определяют астрономическим методом более простым, но с сшибкой (0,3÷0,5˚).

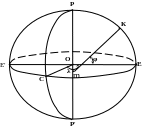
Обозначим буквой К произвольную точку на земном эллипсоиде. Проведем в точке К нормаль к поверхности эллипсоида и отвесную линию.

Геодезическая широта это угол В между нормалью к поверхности эллипсоида в данной точке и плоскостью земного экватора.

Астрономическая широта это угол φ между отвесной линией в данной точке и плоскостью земного экватора.

Г еодезическая долгота L это двугранный угол между плоскостями начального меридиана эллипсоида и меридиана данной точки.

Рис. Геодезические координаты

Рис. Астрономические координаты

Астрономическая долгота λ это двугранный угол между плоскостями начального меридиана и астрономического меридиана данной точки.

Плоскостью астрономического меридиана данной точки называется плоскость, проходящая через отвесную линию в этой точке и параллельная оси вращения Земли.

Е сли в некоторой точке А наблюдалась другая точка земной поверхности. Например, точка В. То угол. Образованный плоскостью астрономического меридиана точки А с вертикальной плоскостью. Проходящей через отвесную линию А и точку В, называется астрономическим азимутом направления АВ (рис 42).

Принято обозначать астрономические координаты и астрономический азимут буквами греческого алфавита:

φ – астрономическая широта,

λ – астрономическая долгота,

α – астрономический азимут.

Отметим еще раз, что астрономические координаты определяются положением отвесной линии в данной точке относительно плоскости экватора и плоскости начального меридиана.

Очевидно, что астрономические координаты это величины, реально существующие в природе.

Геодезические координаты относятся к принятому земному эллипсоиду и определяются в данной точке положением нормали к поверхности эллипсоида относительно плоскости экватора эллипсоида и плоскости начального меридиана эллипсоида (рис 4.3)

На (рис 4.3) a´– проекция на поверхность эллипсоида точки А земной поверхности; a´n – нормаль к поверхности эллипсоида.

Геодезический азимут А - угол, образованный нормальным сечением в данной точке с меридианом в той же точке.

Г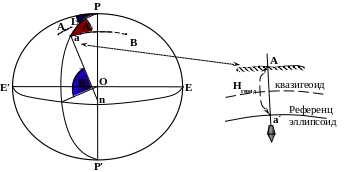 еодезическая широта так же, как и астрономическая, отсчитывается от экватора со знаком плюс к северному полюсу (от 0° до +90°) и со знаком минус – к южному полюсу ( от 0° до -90°); долгота отсчитывается от начального (гринвичского) меридиана на восток со знаком плюс ( от 0° до +180°) и на запад – со знаком минус ( от 0° до -180°).

Рис 43 Геодезические координаты

Территория Украины расположена севернее экватора и восточнее гринвичского меридиана, поэтому знак плюс перед значениями широт и долгот для пунктов, находящихся в пределах территории Украины, не указывается.

Геодезический азимут отсчитывается в данной точке от северной части меридиана по ходу часовой стрелки от 0° до 360° .

Геодезические координаты и азимуты принято обозначать буквами латинского алфавита:

В – геодезическая широта,

L – геодезическая долгота,

А – геодезический азимут.

Геодезические координаты принципиально отличаются от координат астрономических. Тем, что геодезические координаты относятся к абстрактной геометрической фигуре- эллипсоиду. Отсюда очевидно условность геодезических координат; их значения для одних и тех же точек земной поверхности будут различны в зависимости от того, какой будет принят референц-эллипсоид.

Понятно, что геодезические координаты измерять невозможно, их значения получают только путем вычислений по формулам сфероидической геодезии соответственно параметрам принятого референц-эллипсоида и его ориентировки в теле Земли.

При вычислении геодезических координат принимается, что в исходном пункте триангуляции астрономические координаты равны геодезическим, т.е., что отвесная линии по направлению совпадает с нормалью к поверхности референц-эллипсоида. Если принять еще, что поверхность референц – эллипсоида в том же исходном пункте касается поверхности геоида ( или отступает на заданную величину), то тем самым будет осуществлено полное ориентирование референц – эллипсоида в теле Земли.

Итак, считая в одном пункте геодезические координаты известными и принимая измеренное расстояние на физической поверхности за расстояние на поверхности референц – эллипсоида, в другом пункте можем вычислить геодезические координаты.

Отвесная линия, перпендикулярная к поверхности геоида и нормаль, перпендикулярная к поверхности референц – эллипсоида, не совпадают как не совпадают и сами поверхности. Соответствующие углы называются уклонениями отвеса.