12. Нечеткие отношения. Лингвистическая переменная. Нечеткая логика. Построение функций принадлежности.

Нечетким отношением R на множествах Х₁X_2…Х_п называется нечеткое подмножество декартова произведения Х_1*X_2*…*Х_п. Степень принадлежности показывает _R(x₁, x₂..x_n) показывает степень выполнения отношения R между элементами (x₁, x₂..x_n), x_iЄX_i , i=1,n.

В дальнейшем будем рассматривать только бинарные нечеткие отношения, которые задаются на декартовом произведении двух множеств. Обозначим эти множества через X и У. Тогда задание бинарного нечеткого отношения R на Х*У состоит в указании всех троек (x,y, _R(x,y)) где xЄX. уЄY. или, что тоже самое, (x,уЄ ХхУ.

Лингвистической переменной называется переменная, значениями которой могут быть слова или словосочетания некоторого естественного или искусственного языка. Например, лингвистическая переменная «возраст» может принимать следующие значения: «очень молодой», «молодой», «среднего возраста», «старый», «очень старый» и др. Ясно, что переменная «возраст» будет обычной переменной, если ее значения – точные числа, лингвистической она становится, будучи использованной в нечетких рассуждениях человека. Каждому значению лингвистической переменной соответствует определенное нечеткое множество со своей функцией принадлежности.

Нечеткая логика

В обычной (традиионной Аристотелевой) логике существуют только две оценки. Если элемент принадлежит множеству, то 1. если не принадлежит, то 0. Например: есть множество шоколадных конфет. В обычной логике они могут быть либо вкусными, либо нет. т.е. высказывание «Шоколадная конфета вкусная» является либо истинным, либо ложным. А предположим, что конфета - так себе, но невкусной ее все же не назовешь. Как быть? Человек говорит себе так: эта конфета скорее вкусная, чем нет. В этом случае высказывание «Шоколадная конфета вкусная» не может быть абсолютно истинным со значением равным 1. а истинность этого высказывания может быть, например. 0.7.

Нечеткая логика - это разновидность непрерывной логики, в которой логическое формулы могут принимать истинностные значения между 0 и 1. В отличие от вероятностей, которые определяются в статистическом смысле, истинностное значение это некоторое произвольное субъективное значение, не имеющее никакого статистического смысла. Нечеткая логика позволяет приблизить работу компьютеров к мышлению человека.

Построение функций принадлежности.

Задача построения функций принадлежности ставится следующим образом: даны два множества: множество термов L1={l₁ l₂,…,l_m} и универсальное множество U={u₁ u₂,…, u_m}. Нечеткое множество А_j которым описывается лингвистический терм l_j,j=1,m на универсальном множестве U представляется в виде: А_j = { , ,…, } .

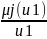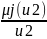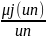Неооходимо определить степени принадлежностей элементов множества U к элементам из множества L, т.е. найти _j(u_i) для всех i = 1,n и j =1, m.

13. Что такое экспертная система? Чем вызван интерес к экспертным системам? Какие задачи относятся к трудноформализуемым? Какими свойствами обладают неформализуемые задачи?

ЭКСПЕРТНАЯ СИСТЕМА [expert system] — компьютерная система, предназначенная для решения качественных задач с помощью накапливаемых знаний и получения логических выводов. Последние могут вырабатываться как с помощью формализации собранной от экспертов-специалистов в данной предметной области информации, так и с помощью извлечения знаний из других информационных источников. Э. с. с успехом применяются в управлении производством и исследовании операций для решения как тактических задач типа составления графика работы оборудования, так и стратегических — планирования, прогнозирования, распределения ресурсов. Э. с. способны фиксировать неудачные решения и учитывать их в дальнейшем, встречаясь с аналогичными задачами. Они оценивают ограничения задачи, и если при этих ограничениях она оказывается неразрешимой, автоматически смягчают их, следуя установленным приоритетам, пока не “выходят” на приемлемые удовлетворительные решения. Применяются разнообразные экономико-математические методы, сети, методы ветвей и границ, стохастические процессы и др. В некоторых достаточно узких областях Э. с. оказываются эффективнее человека-специалиста (как правило, это относится к решению хорошо структурированных задач, поддающихся строгому операциональному описанию, но не кслабо структурированным проблемам).

Разнообразные трудноформализуемые задачи (ТФЗ) в различных предметных областях обладают рядом особенностей: - постановка ТФЗ не может быть полностью формально определена (в числовом виде), а определяется, в основном, в смысловом представлении на профессиональном ограниченном языке; - для ТФЗ характерны неполнота, ошибочность, неоднозначность, неопределенность или противоречивость как исходной информации (знаний и данных), так и используемых правил ее преобразования; - цели решения ТФЗ не могут быть выражены в виде одного четко определенного критерия; - каждая ТФЗ имеет как количественное, так и семантическое решение, представляющее собой значение некоторой переменной, измеряемой, соответственно, в количественных или в семантических шкалах, включая шкалы наименований; - для поиска решений необходимо применять не только алгоритмы, но и эвристическо - эволюционные процедуры и сочетания алгоритмов с такими процедурами; - поиск решений ТФЗ базируется как на использовании известных (или найденных) закономерностей, так и на стратегии здравого смысла или логического вывода и разнообразных эвристических правил для преобразования символов, отображающих понятия (объекты, явления, события и ситуации) данной предметной области. Под эвристическим правилом здесь понимается интуитивное суждение лица, принимающего решение (ЛПР), обеспечивающее поиск рационального решения ТФЗ при резком сокращении множества альтернативных вариантов решения задачи. Можно привести следующие примеры трудноформализуемых (или слабо формализованных) задач: 1) поиск оптимального, в смысле заданного множества критериев, решения на конечном множестве альтернатив; 2) поиск оптимального решения в задачах планирования (операций, компоновки, размещения…); 3) распознавание образов, обработка текстовой и графической информации; 4) определение (идентификация) структуры сложных систем или процессов на основе интерпретации экспериментальных данных; 5) прогнозирование, диагностика состояния и управление относительно несложными дискретными системами; 6) управление сложными системами в условиях неопределенности, в частности, непрерывных технических систем; 7) прогнозирование состояния сложной системы (не обязательно технической) в условиях неопределенности; 8) диагностика причин неправильного функционирования сложной системой (технической и нетехнической) и др. По виду и количеству используемой для принятия решения информации ТФЗ можно классифицировать по схеме, приведенной на рис.1. Из приведенного списка примеров ТФЗ видно, что такие задачи можно разделить на два больших класса: задачи, решение которых не требует математических моделей (ММ), и задачи, решение которых не эффективно без ММ.

Неструктурированная (неформализуемая) задача – задача, в которой невозможно выделить элементы и установить между ними связи.Решение неструктурированных задач из-за невозможности создания математического описания и разработки алгоритма связано с большими трудностями. Возможности использования информационной системы здесь невелики. Решение в таких случаях принимается человеком из эвристических соображений на основе своего опыта и, возможно, косвенной информации из разных источников.