Нейронные сети в пакете matlab План

• Основы реализации нейронных сетей в пакете MATLAB

Введение, биологические нейронные сети, базовая модель нейрона в пакете MATLAB, модель нейронной сети в пакете MATLAB, персептроны и адаптивные линейные фильтры.

• Процедура «обратного распространения» и ее модификации.

Процедура «обратного распространения» и ее модификации. Процедуры улучшения обобщающей способности сети. «Пред» и «пост» обработка сигналов.

• Другие типы сетей.

Радиально-базисные сети. Самоорганизующиеся сети (обучение без учителя). Рекуррентные сети.

• Пользовательские сети.

Введение

Человеческий мозг состоит из множества элементарных частиц, называемых нейронами, реализующих вычисление некоторой параметризированной функции. Результат вычисления этой функции подается на входы других нейронов. Образующееся в результате множество соединенных между собой нейронов, функционирующих как единое целое, называется нейронной сетью.

Специфической особенностью нейронных сетей является способность подстраивать параметры индивидуальных частиц с целью получения оптимального выхода сети. Благодаря огромному количеству нейронов и связей между ними (мозг содержит приблизительно 10¹¹ нейронов и 10¹⁴ синаптических связей), становится возможным вычисление функции практически любой сложности.

Искусственные нейронные сети были созданы, как попытка имитировать работу мозга. Несмотря на то, что первые модели нейронных сетей были весьма грубым приближением, им удалось добиться весьма впечатляющих успехов при решении частных задач – распознавания образов, классификации, предсказания. Можно ожидать, что по мере приближения модели к биологическому оригиналу точность результатов и мощность вычислительного аппарата нейронных сетей будет возрастать.

Модель нейрона

Существует множество моделей нейрона, различающихся в степени соответствия прототипу и его пониманием. Пакет математических вычислений MATLAB реализует простейшую модель нейрона, как элемента, выполняющего взвешенное суммирование сигналов, подаваемых на его входы, прибавление некоторого смещения, а затем обработку полученного значения с помощью функции, называемой функцией передачи.

В нотации, принятой в документации на пакет MATLAB, нейрон можно представить следующей схемой:

Рисунок 2. Модель нейрона в пакете MATALB

где p₁, p₂, ..., p_R – элементы входного вектора

w_1,1, w_1,2, ..., w_1,R – веса входов нейрона

b – смещение нейрона

n – сумма произведений входов (p₁, p₂, ..., p_R) на соответствующие веса (w_1,1, w_1,2, ..., w_1,R) и смещения (b) данного нейрона

a – результат передаточной функции (f) от аргумента (n) – a = f(Wp + b)

R – число входов нейрона

Ввиду того, что представленная выше схема содержит достаточно много деталей, мы, следуя за [1] в дальнейшем изложении будем использовать другой вариант схематического изображения, позволяющий представлять не только отдельные нейроны, но и нейронные сети в целом:

Рисунок 3. Схематическое представление одиночного нейрона

На вход нейрона поступает вектор входных сигналов «p», длина которого равна числу входов (весов) нейрона «R». Затем каждый из элементов входного вектора умножается на соответствующий ему вес «w», полученные произведения складываются, прибавляется смещение «b», и результирующая сумма «n» подается в функцию «f» – передаточную функцию нейрона. Результат вычисления этой функции «a» и является выходом нейрона.

Как правило, используется несколько видов функции передачи – ступенчатая функция, линейная функция, логистическая (сигмоидальная) функция, функция гиперболического тангенса. Однако пакет MATLAB позволяет использовать гораздо более широкий спектр функций, а также создавать пользовательские передаточные функции. Перечислим встроенные функции передачи.

Рисунок 4. Пороговая передаточная функция

Рисунок 5. Симметричная пороговая передаточная функция

Рисунок 6. Логистическая (сигмоидальная) передаточная функция

Рисунок 7. Положительная линейная передаточная функция

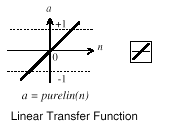
Рисунок 8. Линейная передаточная функция

Рисунок 9. Радиально-базисная передаточная функция

Рисунок 10. Линейная с насыщением передаточная функция

Рисунок 11. Симметричная линейная с насыщением передаточная функция

Рисунок 12. Гиперболический тангенс

Рисунок 13. Треугольная передаточная функция

Помимо описанных, существует также соревновательная функция передачи – при ее использовании выход определяется не для отдельного нейрона, а для всего слоя – обычно на выход подается только сигнал нейрона с наибольшим выходом, а остальные элементы вектора устанавливаются в ноль.

Различные модели нейронов, реализованных в пакете, можно промоделировать, использую демонстрационный пример раздела Toolboxes \ Neural Networks, представленный ниже.

Рисунок 1. Одиночный нейрон (Simple neuron and transfer functions)