18

Лекция №3 Непараметрическое (независящее от распределения) обучение дискриминантных функций

3.1. Пространство весов

Мы уже обсуждали тот факт, что вектор образа X представляется как точка в пространстве образов и что пространство может быть разбито на подобласти для образов, принадлежащих различным категориям. Решающая поверхность, которая делит пространство может быть линейной, кусочно-линейной или нелинейной и может быть в общем виде представлена как:

где и

представляют собой образ и весовой вектор. Проблема обучения системы состоит в том, чтобы найти вектор W, показанный на рис.3.1 на основе априорной информации, полученной от обучающей выборки. Возможно и даже более удобно исследовать поведение обучающих алгоритмов в пространстве весов. Пространство весов есть (n+1) - размерности Эвклидова пространства, в котором координаты ₁ ₂ ... _n+1. Для каждого прототипа , k=1,2,...,M, m=1,2,...,N_k (где M представляет число категорий и N_k представляет собой число прототипов, принадлежащих к категории K, в пространстве W (пространство весов) имеется гиперплоскость, в которой

любой весовой вектор W на положительной стороне гиперплоскости дает w^Тz.. 0. Т.е., если прототип принадлежит категории ₁, любой весовой вектор W на этой стороне гиперплоскости будет вероятно классифицировать . Аналогичные аргументы могут быть рассмотрены для любого весового вектора на другой стороне гиперплоскости, где w^Тz.. 0.

Возьмем 2-х классовую проблему для иллюстрации. Предположим, что мы имеем последовательность N₁ образов, принадлежащих ₁ с общим числом образов N = N₁ + N_l. Предположим также, что ₁ и ₂ -два линейно разделяемых класса. Тогда может быть найден вектор  , такой,что:

и

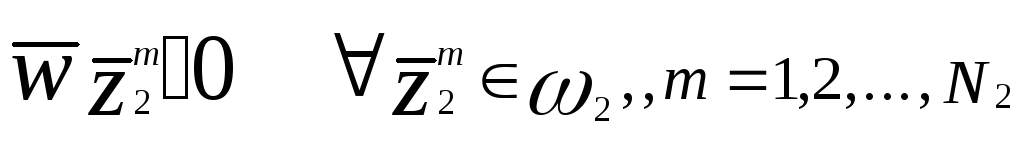
где . и представляют собой категории ₁ и ₂ соответственно.

В общем, для N образов имеется N гиперплоскостей в весовом пространстве. Область решения для категории ₁ в W - пространстве это область, которая лежит на положительной стороне N₁ гиперплоскостей для категории ₁ и на отрицательной для N₂ гиперплоскостей для категории ₂. Предположим, что мы имеем три прототипа Z¹, Z², Z³ и знаем, что все они принадлежат категории ₁ . Три гиперплоскости могут быть нарисованы в W - пространстве, как показано на Рис.3.1а, заштрихованная область на Рис.3.1а показывает решающие области в двухклассовой проблеме. В этой области

и

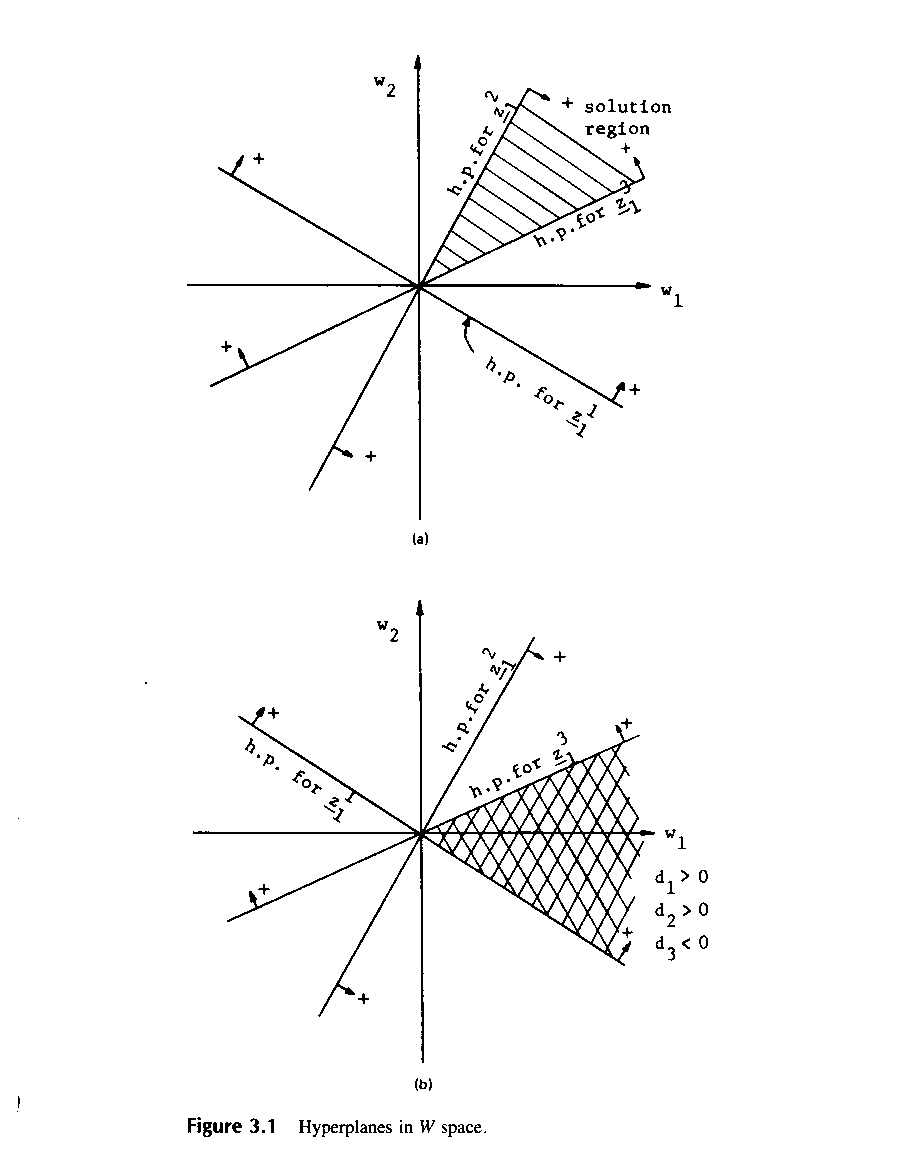
Т.е. любое в этом районе будет вероятно классифицировать прототипы Z¹, Z², Z³ как принадлежащие ₁ , в то время как поперечно заштрихованные области, показанные на рис.3в

d₁

d₂

но d₃ любой  из этой области будет классифицировать Z¹ и Z² как принадлежащий категории ₁ и классифицировать Z³ как относящийся к категории ₂ .

К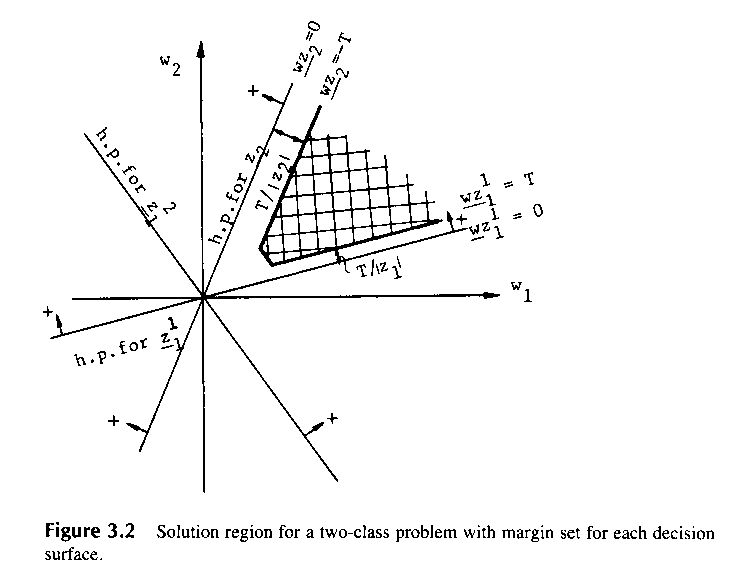 ак обсуждалось в части 2 решающая поверхность для двухклассовой задачи предполагает, что d(w,x) будет больше 0 для всех образов из одного класса и меньше 0 для образов, принадлежащих к другому классу. Но если все заменить на их отрицательные значения - , то решающая поверхность может быть обобщена как часть  пространства, в котором:

^Tz0 ₌ -

наша проблема становится в нахождении , которое обеспечивает положительность всех неравенств.

Иногда может быть желательно иметь ограничение (порог) в дискриминантной функции, такой что:

, (3.6)

где T0 ограничение (порог). Любой , удовлетворяющий неравенству (3.6) является весовым вектором решения. Решающая область теперь изменяется так, как показано на рис.3.2.

В заштрихованной области: оба и - положительные, в то время как отметим, что вдоль исходной гиперплоскости образа

, (3.7)

и что вектор Z (расширенный Z) является перпендикулярным к гиперплоскости и направлен в ее положительную сторону. Тогда линия отстоит от на расстояние . Доказательство этого оставим читателю.