2.1.1 Визначення списку з’єднань та розшарування

Початковими даними для завдання трасування служать списки координат контактів комплексів з деякими можливими додатковими вказівками. Ці списки визначаються після рішення завдань компонування, розміщення і розподіли інваріантних контактів.

Більшість методів трасування являються послідовними, т. е. будуються з'єднання одного комплексу, потім іншого і т. д. Природно, що в цьому випадку важливий порядок трасування комплексів. При До комплексах усього існує K! варіантів їх трасування.

Перебір варіантів трасування можна скоротити, визначивши залежні і незалежні групи комплексів. Залежність двох комплексів частіше усього оцінюються по перекриттю двох мінімальних прямокутників, відповідних комплексів, що покривають контакти. Порядок трасування незалежних комплексів не впливає на конфігурацію їх з'єднань і може бути будь яким. Проте виділити групи незалежних комплексів можна тільки для дуже простих схем. Крім того, навіть розгляд усіх варіантів трасування не може забезпечити отримання оптимальних трас для усіх комплексів, оскільки сам процес трасування залишається послідовним.

На практиці при виборі порядку трасування зв’язків комплексів реальніше використовувати різні оцінки, пов'язані з довжиною з'єднань окремих комплексів, : півпериметр мінімального покриваючого прямокутника або сумарну довжину з'єднань найкоротшого зв'язуючого дерева і число контактів комплексу. Такі оцінки будуються з урахуванням властивостей вживаного алгоритму трасування. У роботі Брэуера [26] показано, що при мінімізації числа не проведених з'єднань доцільно прокладати комплекси в порядку збільшення прийнятої оцінки довжини, а при мінімізації сумарної довжини не проведених з'єднань в порядку зменшення значень цих оцінок.

В деяких випадках для комплексів вказуються пари контактів, що підлягають з'єднанню, т. е. зв'язки. Для з'єднання усіх n контактів комплексу повинно бути вказано n — 1 зв'язків, що утворюють дерево. При трасуванні визначаються траси, т. е. безліч відрізків покриттів, що проводять, і міжшарових переходів, що сполучають контакти комплексу або контакти зв'язку. В процесі трасування утворюються фрагменти ланцюга — підмножини електрично сполучених контактів разом з відрізками трас, що сполучають їх, і міжшаровими переходами. Перед трасуванням кожен фрагмент ланцюга містить один контакт. Для з'єднання двох контактів ланцюга досить визначити трасу, з’єднуюче будь які точки фрагментів, що включають ці контакти. Це вірно, якщо допускається застосування штейнеровских вершин під'єднування, т. е. додаткових вершин під'єднування, відмінних від контактів.

При застосуванні модифікації хвилевого алгоритму вдається досягти добрих результатів, якщо трасування здійснюється для окремих зв'язків різних комплексів з можливим під'єднуванням до вже будованих фрагментам. В цьому випадку завдання визначення порядку трасування зв'язків залишається актуальним.

Для визначення зв'язків (пара контактів, що підлягають з'єднанню) можна застосовувати наступну метрику:

(2.1)

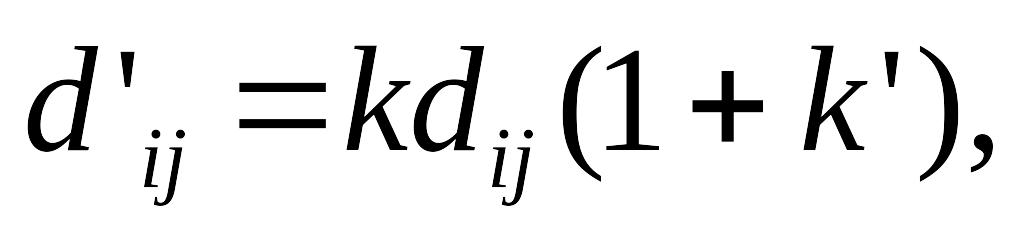
де d'ij довжина з'єднання мінімального в’язучого дерева комплексу між контактами k і dij в вживаною метриці;

(2.2)

де xi, yi, xj, yj,— координати контактів ki, kj;

(2.3)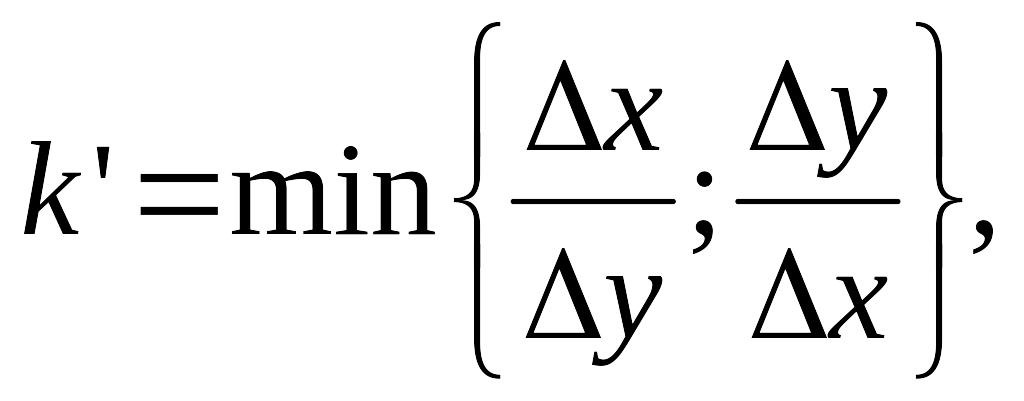

де

(2.4)

k(1коэффициент важливості з'єднання. Значення коефіцієнта встановлюється менше одиниці для зв’язків таких ланцюгів, які повинні проводитися в першу чергу, т. е. коли необхідно отримати трассы мінімальної довжини.

Мінімальне зв’язуючи дерево у вживаній метриці визначається за допомогою алгоритму Прима [17]. Зв'язки упорядковуються в порядку збільшення довжини d'ij (2.1). Отже, дані для трасування формуються у вигляді впорядкованого по декількох параметрах списку зв'язків. При впорядковуванні враховує призначення і тип з'єднання (коефіцієнт k), його довжину в прямокутній метриці (dij) і прямолінійності (k').

Відомі багатошарові конструкції (зокрема, плати з відкритими контактними майданчиками), де не допускається застосування додаткових міжшарових переходів.

Найтривалішим рішенням задачі розшарування для таких конструкцій є наступне. Проводиться трасування усіх з'єднань в першому шарі. Залишені не проведені з'єднання трасуються в другому шарі і т. д. Проте в цьому випадку часто виходить велике число шарів і нерівномірне їх заповнення.

Тому представляє інтерес розбиття безлічі з'єднань схеми на підмножини, які проводяться в одному шарі, т. е. до трасування повинно бути указано, які з'єднання проводити в кожному шарі. Для вирішення завдання розбиття можна використовувати методи визначення планарності графів, серед яких по ефективності виділяються циклічні методи [15]. Суть цих методів полягає в наступному. У графі визначається цикл (у окремому випадку гамильтонов), за допомогою якого початковий граф спрощується і виходить декілька під графів. Потім за властивостями цих під графів встановлюється планарності цього графа. Якщо граф планарен, вирішується завдання його плоскої реалізації.

Разом з цінними властивостями циклічні методи мають істотний недолік: знаходження потрібного циклу може виявитися трудомістким, а іноді взагалі не вирішуваною проблемою. Крім того, реалізація планарного графа на площині з урахуванням метричних обмежень представляє чималі труднощі. Тому використання цих методів для вирішення практичних задач обмежено.

Спрощено завдання розшарування можна представити у такому вигляді. Для кожного ланцюга будуються траси зв’язків в одній площині. Визначаються перетини окремих з'єднань різних ланцюгів. Тоді завдання розбіенія пересічних з'єднань на різні шари з мінімізацією числа шарів можна вирішити, застосувавши процедуру Вейссмана [4].

Результати можна поліпшити, якщо об'єднати задаючи розшарування і побудови зв'язуючих дерев.

Розглянемо тільки найкоротші траси з'єднань. При з'єднанні двох контактів найкоротшою трасою буде відрізок прямої, проведеної через місце розташування контактів. Якщо число контактів комплексу i рівне ni, то число всіляких найкоротших трас, що сполучають пари контактів комплексу, дорівнює числу ребер у відповідному повному графові, т. е. _.

З усіх цих трас для реалізації зв'язуючого дерева потрібні ni 1 найкоротших трас.

Найкоротші траси для зв'язуючих дерев комплексів можна вибрати за допомогою алгоритму [2].

При визначенні конфігурацій зв'язуючих дерев усіх комплексів переслідуються дві мети: мінімальності числа шарів і мінімальність сумарної довжини комутацій.

Алгоритм досить універсальний в тому сенсі, що окрім найкоротших тут можуть досліджуватися і будь які інші траси заздалегідь заданої форми, наприклад: ортогональні траси, траси з обходом перешкод і т. д.

Проте загальновідомі труднощі, пов'язані з великим об'ємом обчислень процедури Вейссмана [4]. Тому на практиці доцільніше користуватися більш простою процедурою, що дозволяє отримати розбієніє усіх з'єднань схеми на задане число шарів, а потім прокладати траси у встановлених шарах.

Для визначення наявності перетинів двох зв’язків різних ланцюгів кожне з'єднання деяким чином має бути відображене на площині. Відомо декілька підходів для представлення з'єднань на площини і визначення їх перетинів.

1. З'єднання представляються у вигляді прямолінійних відрізків і їх перетину перевіряються по рівнянням прямих або іншими способами.

2. З'єднання представляються у вигляді прямокутників, що покривають точки, що сполучаються, і перевіряється їх перекриття.

3. З'єднання відображуються на прямокутну решітку.

Основний недолік цих підходів полягає в тому, що при представленні з'єднань вищезгаданими способами число перетинів виходить завищеним. Поняття «Перетин з'єднань» зазвичай розцінюється як неможливість проведення цих з'єднань в одній площині, хоча така можливість іноді існує. З іншого боку, отримане розшарування при такій інтерпретації з'єднань ще не гарантує плоскої реалізації з'єднань в кожному шарі. Проте представляє інтерес отримати таке розшарування, при якому труднощі плоскої реалізації з'єднань були б мінімальними.

Розглянемо завдання розшарування, коли з'єднання представляються у вигляді прямолінійних відрізків. Якщо такі два з'єднання перетинаються, можна вважати, що між ними потенційно існує конфлікт. Очевидно, що якщо неможливо побудувати неприкосновених траси двох з'єднань, то відповідні ним відрізки обов'язково перетинаються.

При цьому завдання розшарування можна представити таким чином. Будується граф перетинів зв’язку. Кожному з'єднанню відповідає вершина графа. Дві вершини з'єднуються ребром, якщо пересікаються прямолінійні відрізки відповідних зв’язків. Вимагається розбити безліч вершин отриманого графа k підмножин S1, S2, ., Sn таким образом, щоб сумарне число ребер між вершинами

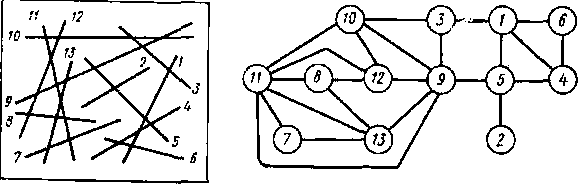
Рисунок 2.1

Безліч з'єднань, представленних у вигляді прямолінійних відрізків, і відповідний граф перетинів

кожної підмножини було мінімальним. Це відповідає розбиттю безлічі з'єднань на k шарів з мінімальним числом перетинів.

При такій постановці завдання розшарування можливий наступний шлях її рішення [28].

З графа перетинів виключається вершина з інцидентними їй ребрами, міра якої менше k. Природно, для такої вершини завжди знайдеться підмножество, з вершинами якого вона не має загальних ребер. Після виключення однієї вершини це правило застосовується для інших, поки міри усіх залишившихся вершин стає не менше k. Виключені вершини складають окремий список S. Необхідно відмітити, що порядок наступного включення вершин списку S в підмножини S1, S2, ...__

У підмножину S1 включаються вершини, складова внутрішньо стійка безліч вершин отриманого графа перетинів. Для визначення внутрішньо стійкої великої кількості на кожному кроці виділяється вершина графа перетинів з максимальною мірою і виключається з графа разом з інцидентними їй ребрами. Вершини виключаються до тих пір, поки в графі не залишиться жодного ребра. Виключені вершини разом з ребрами між ними складають новий граф перетинів.

Аналогічно визначається підмножина вершин S2, тільки в цьому випадку в список S включаються вершини, міри яких менше числа k 1.

Після визначення k ої підмножини Sk ще може залишитися не порожній граф перетинів. Позначимо список вершин цього графа S'. Далі вершини із списку S по черзі в заданому порядку (зворотному порядку включення в цей список) включаються в ті підмножества S ₁, S2, .., Sk, з вершинами яких вони не мають загальних ребер в початковому графові перетинів. Вершини із списку S' включаються в ті підмножини, з вершинами яких вони мають найменше число загальних ребер. Якщо це число однакове для декількох підмножеств, вибирається підмножина з найменшим числом вершин.