Расчет многопролетной статически определимой балки.
Определение реакций в опорах балки путем разделения многопролетной балки на составные балки
Исходные данные: M= 60 кНм, P= 20 кН, q=40 кН/м, l= 2 м, k = 1,5.
Рис. 4. Схема многопролетной балки
Многопролетная балка имеет основную балку с тремя опорными стержнями
(условие 1 способа образования многопролетных балок); соединяемая с по-
мощью шарнира последующая балка опирается на дополнительный опорный
стержень (условие 2 способа образования многопролетных балок). Степь неопределимости системы w равна 0.
Число неизвестных реакций связей равно числу опорных стержней C 0
многопролетной балки, т. е. равно 5. А для плоской системы сил, действую-
щих на многопролетную балку, можно составить только три уравнения рав-
новесия. Естественно поэтому при определении реакций связей стремление
расчленить систему в шарнирных соединениях и образовать отдельные балки,
построив поэтажную схему взаимодействия балок (рис. 5).
Рис. 5. Поэтажная схема взаимодействия балок
На нижнем уровне поэтажной схемы располагается балка, установленная
на трех опорных стержнях (балка АВС), на следующих более высоких уров-
нях располагаются балки СЕ и ЕF.
При построении поэтажной схемы взаимодействие балок заменено вве-
дением соответствующих неизвестных пока реакций связей:H C ,V C – реак-
ции, определяющие взаимодействие балок АВС и СЕ; HE ,V EV – реакции, оп-
ределяющие взаимодействие балок СЕ и ЕF.
При изображении направления одноименных реакций следует обращать
внимание, что эти реакции должны иметь противоположные направления при
приложении их к взаимодействующим балкам. Например, реакции HC иV C ,
приложенные в точке С к балке СЕ, противоположно направлены реакциям HC и VC , приложенным в точке С к балке АВС. Реакции HE и VE , приложен-
ные в точке Е к балке ЕF, противоположно направлены реакциям HE и VE,
приложенным в точке Е к балке СЕ.
При разбиении многопролетной балки на n составных балок мы можем
составить 3n уравнений равновесия (по три для каждой балки). Число неиз-
вестных реакций связей при этом будет равно числу опорных стержней C0
плюс 2p реакций связей (по две на каждое шарнирное соединение) при раз-
делении многопролетной балки в шарнирных соединениях.
Для определения неизвестных реакций необходимо, чтобы число уравне-
ний равновесия было равно числу неизвестных:
Так как для статически определимой геометрически неизменяемой многопро-
летной балки условие обеспечивается, то поставленная задача по
определению опорных реакций разрешима.
Рис. 6. Поэтажная схема взаимодействия балок с заменой опорных стержней
реакциями связей
Начинать расчет следует с балки верхнего уровня (балки ЕF). В этом
случае для определения реакций HE , VE и VF (рис. 6) можно использовать
следующие уравнения равновесия:
- сумма проекций на ось х всех сил, действующих на балку ЕF, равна нулю
- сумма моментов всех сил, действующих на балку ЕF, относительно точки Е
равна нулю
- сумма моментов всех сил, действующих на балку ЕF, относительно точки
F равна нулю
Проведем проверку правильного определения реакций, используя урав-
нение равновесия в виде суммы проекций на ось y сил, действующих на бал-
ку ЕF:
Далее переходим к расчету балки следующего уровня (балки СЕ, рис.6).
Реакции HE и VE уже определены. А для расчета реакций HC ,V C иV D вновь
используем три уравнения равновесия:
- сумма проекций на ось х всех сил, действующих на балку СЕ, равна нулю
- сумма моментов всех сил, действующих на балку СЕ, относительно точки С
равна нулю
Откуда
- сумма моментов всех сил, действующих на балку СЕ, относительно точки
D равна нулю
Проведем проверку правильного определения реакций, используя урав-
нение равновесия в виде суммы проекций на ось y сил, действующих на
балку СЕ:
Далее переходим к расчету балки нижнего уровня (балки АВС, рис. 6).
Реакции HC и VC уже определены. А для расчета реакций HB ,V B и V A вновь
используем три уравнения равновесия:
сумма проекций на ось х всех сил, действующих на балку АВС, равна нулю
- сумма моментов всех сил, действующих на балку АВС, относительно точки
A равна нулю
Откуда
- сумма моментов всех сил, действующих на балку АВС, относительно точки
B равна нулю
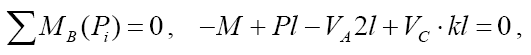
Откуда
Проведем проверку правильного определения реакций, используя урав-
нение равновесия в виде суммы проекций на ось y сил, действующих на бал-
ку АВС:
Изобразим теперь расчетную схему многопролетной балки, заменив дей-
ствие опорных стержней реакциями связей VA ,H B , VB ,V D и VF (рис. 7).
Рис. 7. Схема многопролетной балки с заменой опорных стержней реакциями связей
Проведем проверку правильного определения реакций, используя урав-
нение равновесия в виде суммы проекций на ось y сил, действующих на всю
многопролетную балку:
ПРИМЕЧАНИЕ: расчет многопролетной рамы можно произвести также по принципу возможных перемещений.