Текст пособия Введение.

Деятельность отдельных людей и коллективов, как правило, связана с выбором таких решений, которые позволили бы получить некие оптимальные результаты–достичь максимальной прибыли предприятия, закончить комплекс работ в кратчайший срок, соединить компьютеры локальной сетью минимальной длины и т. д. Во всех этих задачах можно выделить цель ( в математике она записывается в виде целевой функции, которую необходимо исследовать на минимум или максимум, то есть, оптимизировать). Кроме того, в каждой такой задаче существуют ограничения, которые тоже можно записать в математических терминах. В этом случае говорят, что построена математическая модель изучаемого явления. Итак:

Математической моделью называют приближенное описание некоторого явления внешнего мира, записанное с помощью математической символики.

Перечисленные выше задачи относятся к оптимизационным задачам (ищется оптимальное решение, при котором целевая функция достигает минимума или максимума). Выработаны специальные методы решения таких задач, которые носят название линейного, или математического программирования. Эти методы применялись, например, во время второй мировой войны для планирования военных операций, поэтому соответствующая наука долгое время называлась «исследование операций». В настоящее время применяется термин «теория принятия решений» и методы этой науки применяются очень широко для решения разнообразных задач в различных областях.

Мы будем рассматривать специфические задачи теории принятия решений, связанные с применением математической теории графов.

Понятие графа

Великий математик Л. Эйлер в 1736 году писал: «Мне была предложена задача об острове, расположенном в городе Кенигсберге и окруженном рекой, через которую перекинуто 7 мостов.

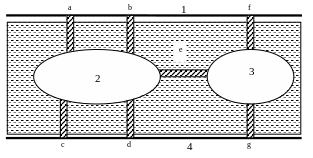
Рис. 1.

Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост. И тут же мне было сообщено, что никто до сих пор не смог этого проделать, но никто и не доказал, что это невозможно. Вопрос этот, хотя и банальный, показался мне достойным внимания тем, что для его решения недостаточны ни геометрия, ни алгебра, ни комбинаторное искусство. После долгих размышлений я нашел легкое правило, основанное на вполне убедительном доказательстве, при помощи которого можно во всех задачах такого рода тотчас же определить, может ли быть совершен такой обход через какое угодно число и как угодно расположенных мостов или не может».

Город Кенигсберг располагается на обоих берегах реки Прегель и на двух островах, которые соединялись семью мостами. На рис. 1. изображен план реки и мостов, соединяющих берега реки и два острова.

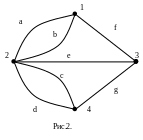Эту же схему можно изобразить, «сжав» берега реки и два острова в точки (вершины), а мосты «растянуть» в линии (ребра). Полученная фигура называется графом (см. рис.2).

Можно показать, например, перебрав все варианты, что изображенную фигуру нельзя обвести острием карандаша, не отрывая его от бумаги и проходя по каждой дуге ровно один раз (попробуйте). Немного позднее мы покажем, как в общем виде решается подобная, но более общая задача, которая носит название задачи коммивояжера.

Мы подошли к тому, чтобы дать основные понятия графа, классификацию графов и способы описания графа.

Определение: Графом называется множество точек плоскости или пространства (вершины графа) и множество отрезков, их соединяющих (дуги, если указано направление отрезка, ребра в противном случае).

Граф называется ориентированным, если он состроит из вершин и дуг и неориентированным, если он состоит из вершин и ребер (см. рис. 3а, 3б).

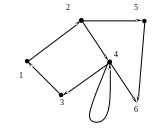
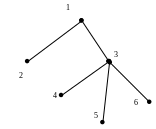
Рис.3а. Рис.3б.

Рассматриваются также смешанные графы – графы, состоящие из ребер и дуг (приведите пример). Поскольку расположение вершин графа и форму дуг и ребер можно выбирать произвольно, то один и тот же граф можно изобразить по-разному. Такое свойство графа называется изоморфизмом.

Определение: Маршрутом, или путем, соединяющим вершины А и В графа, называется такая последовательность ребер, в которой каждые два ребра имеют общую вершину, причем первое ребро выходит из вершина А, а последнее входит в вершину В. В этом случае вершины А и В называются связанными. Граф называется связным, если любая пара его вершин связана.

Граф, представленный на рис.4а является связным, на рис. 4б. – несвязным.

A

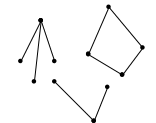
Рис.4а. Рис.4б.

Определение: Маршрут называется цепью, если каждое ребро графа встречается в нем не более одного раза (вершины в цепи могут повторяться). Цепь, начальная и конечная вершины которой совпадают, называется циклом.

Например, на рис. 4а цепь, связывающая вершины А и В, проходит по ребрам 1-2-3-4-5-6-7. Цикл, выходящий из вершины В, отмечен перечеркнутыми ребрами.

Определение: Вершина называется четной, если в ней сходится четное число ребер и нечетной, если в ней сходится нечетное число ребер. Число ребер, сходящихся в вершине графа, называется степенью (порядком) этой вершины. Граф называется конечным, если множество его ребер конечно.

Например, вершина А на рис. 4а является четной (ее степень равна 2), вершина В является нечетной (ее степень равна 3).

Возвратимся к задаче о Кенигсбергских мостах. Решая ее, Эйлер доказал следующую теорему.

Теорема (Эйлер). В связном конечном графе существует цикл, содержащий все ребра графа тогда и только тогда, когда все вершины графа четные.

Такой цикл называют эйлеровым циклом, а граф, у которого существует эйлеров цикл – эйлеровым графом.

Покажем на примере, как построить эйлеров цикл в эйлеровом графе. Рассмотрим эйлеров граф (убедитесь в том, что все вершины его четные).

Выберем любую вершину, например, вершину А и найдем произвольный цикл. Может быть два случая: либо цикл полный, то есть, проходит через все ребра и тогда задача решена. Может быть и так, что цикл не проходит через все ребра. Например, цикл 1-2-3-4-5. На рис. 5б отмечены эти ребра и для наглядности заштрихована внутренняя часть этого цикла.

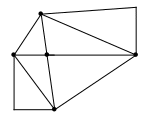
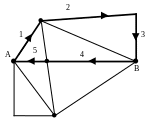
Рис. 5а. Рис. 5б.

Обязательно найдется вершина, из которой выходят еще не отмеченные ребра (их окажется четное число). Выберем, например, вершину В и найдем цикл. На рис.5в он отмечен как 6-7-8-9 и для наглядности заштрихована внутренняя область.

Объединим два цикла следующим образом. Выходим из вершины А и доходя до вершины В, проходим цикл, выходящий из этой вершины, возвращаемся в вершину В и проходим дальше цикл до вершины А. получим: 1-2-3-6-7-8-9-4-5.

Затем выбираем вершину, например, С и находим цикл 10-11-12. Он отмечен на рис.5г.

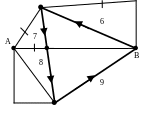
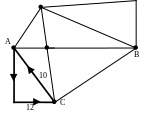
Рис. 5 в. Рис.5 г.

Объединим три цикла и получим окончательный ответ:

1-2-3-6-7-8-10-11-12-9-4-5.