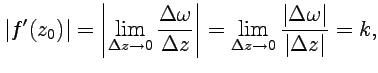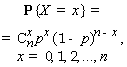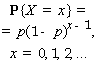Понятие об уравнениях в частных производных.
Пусть
искомая функция ![]() зависит
от нескольких независимых переменных
зависит
от нескольких независимых переменных ![]() (
(![]() ).
Уравнение, связывающее искомую функцию,
независимые переменные и частные
производные от искомой функции,
называется дифференциальным уравнением
с частными производными. Оно имеет вид:
).
Уравнение, связывающее искомую функцию,
независимые переменные и частные
производные от искомой функции,
называется дифференциальным уравнением
с частными производными. Оно имеет вид:
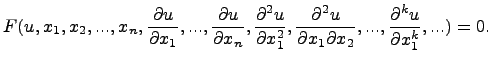
Здесь ![]() --
данная функция своих аргументов. Порядок
старшей частной производной, входящей
в уравнение, называется порядком
уравнения частными производными.
--
данная функция своих аргументов. Порядок
старшей частной производной, входящей
в уравнение, называется порядком
уравнения частными производными.
Дифференциальное
уравнение с частными производными
первого порядка с ![]() независимыми
переменными может быть записано в форме:
независимыми
переменными может быть записано в форме:
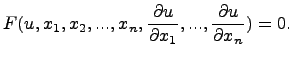
Общее решение дифференциального уравнения с частными производными, вообще говоря, может зависеть от некоторых произвольных (гладких) функций.
Краевая задача.
Краевая задача — дифференциальное уравнение (система дифференциальных уравнений) с заданными линейными соотношениями между значениями искомых функций на начале и конце интервала интегрирования.
Решение краевой задачи ищется в виде суммы линейной комбинации решений однородных задач Коши, соответствующих заданному уравнению при линейно независимых векторах начальных условий, и решения неоднородной задачи Коши с произвольными начальными условиями.
Пример краевой задачи:
![]()
(система неоднородных обыкновенных
дифференциальных уравнений с
переменными коэффициентами, заданная
на участке ![]() )
)
Граничные
условия (общий вид для
всех краевых задач): ![]()
Где ![]() —
матрицы,
—
матрицы, ![]() —
вектор неизвестных,
—
вектор неизвестных, ![]() —
— ![]() -вектор
(делающий систему неоднородной),
-вектор
(делающий систему неоднородной), ![]() —
-вектор
—
-вектор
Общий вид решения:![]()
Удовлетворение граничных условий
достигается за счёт подбора коэффициентов ![]() .
Эти коэффициенты находятся путём решения
системы линейных уравнений.
.
Эти коэффициенты находятся путём решения
системы линейных уравнений.
Уравнение колебаний.
Волновое уравнение в математике — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно линейная: звук в газах, жидкостях и твёрдых телах) и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн.
Уравнение теплопроводности.
t=f(x,y,z,τ),
где:t–температура_тела; x,y,z-координаты_точки; τ-время. Такое температурное поле называется нестационарным ∂t/∂ 0, т.е. соответствует неустановившемуся тепловому режиму теплопроводности Если температура тела функция только координат и не изменяется с течением времени, то температурное поле называется стационарным:t = f(x,y,z) , ∂t/∂ = 0
Понятие функции комплексной переменной. Предел и непрерывность.


Производная функция комплексной переменной.
Производной от однозначной функции w = f(z) в точке z называется предел:

Геометрический смысл аргумента и модуля производной. Условия Коши-Римана.
Условия
Коши — Римана,
называемые также условиями
д’Аламбера — Эйлера —
соотношения, связывающие вещественную ![]() и
мнимую
и
мнимую ![]() части
всякой дифференцируемой функции
комплексного переменного
части
всякой дифференцируемой функции
комплексного переменного ![]() .
.
геометрический смысл аргумента
производной состоит в том, что ![]() равен
разности углов касательных к кривой
равен
разности углов касательных к кривой ![]() и
ее образу
и
ее образу ![]() в
точках, связанных условием
в
точках, связанных условием ![]() .
Рассматривая две кривых
.
Рассматривая две кривых ![]() ,
а также их образы
,
а также их образы ![]() ,
легко показать с помощью (38),
что
,
легко показать с помощью (38),
что
|
(38) |
т. е. углы между кривыми на комплексной
плоскости и их образами в точке
не
изменяются в случае, если ![]() .
Такое свойство называется свойством
сохранения углов. Геометрический
смысл модуля производной следует из
соотношения:
.
Такое свойство называется свойством
сохранения углов. Геометрический
смысл модуля производной следует из
соотношения:
|
(39) |
которое означает, что ![]() является коэффициентом
растяжения в точке
является коэффициентом
растяжения в точке ![]() при
отображении с помощью функции
при
отображении с помощью функции ![]() .
.
Преобразование Лапласа.
Преобразование Лапласа - интегральное преобразование, связывающее функцию F(p) комплексного переменного (изображение) с функцией f(x) действительного переменного (оригинал).
Преобразованием Лапласа от функции f(x) (оргигинала) называется функция:

f(x) называют оригиналом преобразования Лапласа, а F(p) - изображением преобразования Лапласа.
Понятие оригинала, изображения.
Функция-оригинал —
фундаментальное понятие в операционном
исчислении; для того, чтобы
функция ![]() могла
называться оригиналом, она должна
удовлетворять трем условиям:
могла
называться оригиналом, она должна
удовлетворять трем условиям:
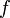 удовлетворяет условию
Гёльдера почти всюду
на вещественной прямой
удовлетворяет условию
Гёльдера почти всюду
на вещественной прямой 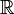 ,
притом на произвольном
конечном интервале
,
притом на произвольном
конечном интервале 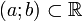 множество точек,
в которых указанное условие не
выполняется, конечно, притом в этих
точках она должна претерпевать разрыв
1-го рода. Формально, для
произвольного
множество точек,
в которых указанное условие не
выполняется, конечно, притом в этих
точках она должна претерпевать разрыв
1-го рода. Формально, для
произвольного 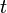 ,
не относящегося к упомянутому множеству,
должны существовать положительные
постоянные
,
не относящегося к упомянутому множеству,
должны существовать положительные
постоянные 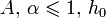 ,
такие, что
,
такие, что 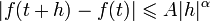 для
произвольного
для
произвольного 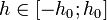 .
.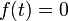 при
при 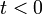 .
.на функцию
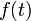 накладывается
определённое ограничение — она должна
возрастать не быстрее показательной
функции. Формально, для
этой функции должны существовать
постоянные
накладывается
определённое ограничение — она должна
возрастать не быстрее показательной
функции. Формально, для
этой функции должны существовать
постоянные 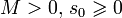 такие,
что
такие,
что 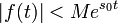 для
произвольного
для
произвольного 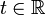 .
.
Изображением
по Лапласу функции-оригинала f (t) (или
преобразованием Лапласа функции f (t))
называется функция комплексной
переменной p, определяемая
равенством
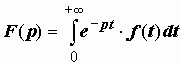 .
.
Понятие о свойствах изображения и оригинала.
Отметим некоторые свойства изображений и оригиналов.
Теорема подобия. Если изображение
функции ![]() равно
равно ![]() ,
то изображение функции
,
то изображение функции ![]() равно
равно ![]() .
.
Линейность изображения. Изображение суммы нескольких функций, умноженных на постоянные, равняется сумме изображений этих функций, умноженных на соответствующие постоянные.
Дифференцирование изображения. Если F(p) является
изображением функции f(t), то ![]() является
изображением функции
является
изображением функции ![]() ,
то есть умножению оригинала на tсоответствует
умножение изображения на –1 и
дифференцирование его по p.
,
то есть умножению оригинала на tсоответствует
умножение изображения на –1 и
дифференцирование его по p.
Теорема смещения. Умножению оригинала
на ![]() соответствует
запаздывание изображения на , то
есть
соответствует
запаздывание изображения на , то
есть ![]() или
или ![]() .
.
Изображение производных. Если ![]() являются
функциями-оригиналами и f(t)
являются
функциями-оригиналами и f(t)![]() F(p),
то
F(p),
то

Теоремы запаздывания и опережения оригинала.
Запаздывание оригиналов и изображений. Предельные теоремы
Запаздывание изображения:
![]()
![]()
Запаздывание оригинала:
![]()
![]()
Примечание: ![]() — функция
Хевисайда.
— функция
Хевисайда.
Свойство линейности изображения.
Линейность изображения. Изображение суммы нескольких функций, умноженных на постоянные, равняется сумме изображений этих функций, умноженных на соответствующие постоянные.
Теорема подобия.
Теорема подобия. Если изображение функции равно , то изображение функции равно .
Теорема смещения изображения.
Теорема смещения. Умножению оригинала на соответствует запаздывание изображения на , то есть или .
Дифференцирование оригинала и изображения.
Дифференцирование изображения. Если F(p) является изображением функции f(t), то является изображением функции , то есть умножению оригинала на t соответствует умножение изображения на –1 и дифференцирование его по p.
Интегрирование оригинала и изображения.
Интегрирование оригинала
Если ![]() то
то 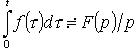
Интегрирование изображения
Если 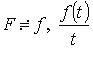 -
оригинал, то
-
оригинал, то 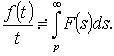
Свертка функций.
Изображение свертки (теорема умножения)
Если ![]() то
то
![]()
Умножение изображений
Умножение изображений
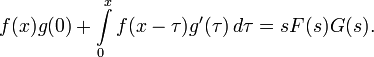
Решение линейных дифференциальных уравнений с постоянными коэффициентами операционным методом.
Решение систем линейных дифференциальных уравнений методами операционного исчисления.
Основные понятия и формулы комбинаторики.
Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Приведем наиболее употребительные из них.
Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок
Pn = n!,
где n! = 1 * 2 * 3 ... n.
Заметим, что удобно рассматривать 0!, полагая, по определению, 0! = 1.
Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений
Amn = n (n - 1)(n - 2) ... (n - m + 1).
Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний
С mn = n! / (m! (n - m)!).
Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством
Amn = PmC mn.
Pn (n1, n2, ...) = n! / (n1! n2! ... ),
где n1 + n2 + ... = n.
При решении задач комбинаторики используют следующие правила:
П р а в и л о с у м м ы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.
П р а в и л о п р о и з в е д е н и я. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.
Предмет теории вероятностей. Основные понятия. Классификация событий.
Тео́рия вероя́тностей — раздел математики, изучающий закономерности случайных явлений:случайные события, случайные величины, их свойства и операции над ними.
Вероя́тность (вероятностная мера) — численная мера возможности наступления некоторого события.
Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.
Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.

Классическое, статистическое и геометрическое определения вероятности.
Согласно геометрическому определению,
вероятность случайного события А равна отношению меры области, благоприятствующей появлению события А, к мере всей области, т.е.
![]() .
.
статистическая вероятность случайного события А равна относительной частоте появления этого события в ряде испытаний, т.е.
![]() ,
,
где m – число испытаний, в которых появилось событие А;
n – общее число испытаний.
Вероятностью P(A) события в данном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий:
![]()
Простейшие свойства вероятности.
Пусть ![]() и
и ![]() --
некоторые события, т.е.,
--
некоторые события, т.е., ![]() .
Имеют место следующие свойства.
.
Имеют место следующие свойства.
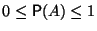 ,
,  ,
,  .
.Если
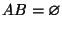 ,
то
,
то
![]()
В общем случае (если не предполагать, что )
![]()
Пересечение множеств (произведение событий). Теорема умножения вероятностей.
Пересечением множеств A и B называется
множество элементов, принадлежащих
одновременно и A и B.
Обозначают ![]() и
читают "пересечение A и B".
и
читают "пересечение A и B".
Теорема умножения. Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.
P(AB)=P(A)PA(B) |
Объединение множеств (сумма событий). Теорема сложения вероятностей, ее следствия.
Объедине́ние
мно́жеств (тж. су́мма или соедине́ние)
в теории
множеств —
множество, содержащее в себе все элементы
исходных множеств. Объединение двух
множеств ![]() и
обычно
обозначается
и
обычно
обозначается ![]() ,
но иногда можно встретить запись в виде
суммы
,
но иногда можно встретить запись в виде
суммы ![]() .
.
Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:
![]()
Следствие 1.
Если события ![]() образуют
полную группу несовместных событий, то
сумма их вероятностей равна единице:
образуют
полную группу несовместных событий, то
сумма их вероятностей равна единице:
![]() .
.
Следствие 2. Сумма вероятностей противоположных событий равна единице:
![]() .
.
Формула полной вероятности.
Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2, ..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A, ..., HnA. Следовательно,
![]()
Применяя аксиому сложения вероятностей, имеем
![]() Но
Но ![]() (i=1,
2, ..., n), поэтому
(i=1,
2, ..., n), поэтому
|
Формула Байеса.
Формула Байеса:
![]() ,
,
где
![]() —
априорная вероятность гипотезы A (смысл
такой терминологии см. ниже);
—
априорная вероятность гипотезы A (смысл
такой терминологии см. ниже);
![]() —
вероятность гипотезы A при
наступлении события B (апостериорная
вероятность);
—
вероятность гипотезы A при
наступлении события B (апостериорная
вероятность);
![]() —
вероятность наступления события B при
истинности гипотезы A;
—
вероятность наступления события B при
истинности гипотезы A;
![]() —
полная вероятность наступления события B.
—
полная вероятность наступления события B.
Повторение независимых испытаний. Формула Бернулли.
Примеры повторных испытаний:
1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;
2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается).
Теорема: Если
Вероятность p наступления
события Α в
каждом испытании постоянна, то
вероятность ![]() того,
что событие A наступит k раз
в n независимых
испытаниях, равна:
того,
что событие A наступит k раз
в n независимых
испытаниях, равна: ![]() ,
где
,
где ![]() .
.
Локальная, интегральная теорема Лапласа.
Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)
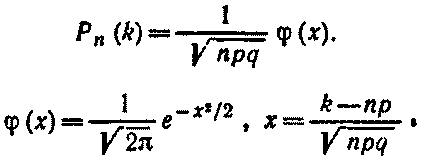
Для определения значений φ(x) можно воспользоваться специальной таблицей.
Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k1 раз и не более k2 раз, приближенно равна
P(k1;k2)=Φ(x'') - Φ(x')
Здесь
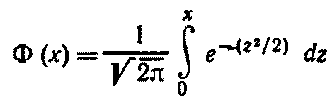
-функция Лапласа
![]()
Значения функции Лапласа находят по специальной таблице.
Формула Пуассона.
При большом числе испытаний n и
малой вероятности р формулой
Бернулли пользоваться неудобно,
например, ![]() вычислить
трудно. В этом случае для вычисления
вероятности того, что в n испытаниях
(n – велико) событие произойдет k раз,
используют формулу Пуассона:
вычислить
трудно. В этом случае для вычисления
вероятности того, что в n испытаниях
(n – велико) событие произойдет k раз,
используют формулу Пуассона:
![]() –
среднее число появлений события
в n испытаниях.
–
среднее число появлений события
в n испытаниях.
Эта формула дает удовлетворительное
приближение для ![]() и
и ![]() .
.
Производящая функция.
Производя́щая фу́нкция последовательности ![]() —
это формальный
степенной ряд
—
это формальный
степенной ряд
![]() .
.
Зачастую производящая функция последовательности чисел является рядом Тейлора некоторой аналитической функции, что может использоваться для изучения свойств самой последовательности. Однако, в общем случае производящая функция не обязана быть аналитической. Например, оба ряда
![]() и
и ![]()
имеют радиус сходимости ноль, то есть расходятся во всех точках, кроме нуля, а в нуле оба равны 1, то есть как функции они совпадают; тем не менее, как формальные ряды они различаются.
Случайные величины, виды, способы задания.
Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.
Случайные величины могут принимать дискретные, непрерывные и дискретно-непрерывные значения. Соответственно случайные величины классифицируют на дискретные, непрерывные и дискретно-непрерывные (смешанные). На схеме испытаний может быть определена как отдельная случайная величина (одномерная/скалярная), так и целая система одномерных взаимосвязанных случайных величин (многомерная/векторная).
Функция распределения случайной величины и ее свойства.
Фу́нкция распределе́ния в теории вероятностей — функция, характеризующая распределение случайной величины или случайного вектора.
Пусть дано вероятностное
пространство ![]() ,
и на нём определена случайная
величина
,
и на нём определена случайная
величина ![]() с
распределением
с
распределением ![]() .
Тогда функцией распределения случайной
величины
называется функция
.
Тогда функцией распределения случайной
величины
называется функция ![]() ,
задаваемая формулой:
,
задаваемая формулой:
![]() .
.
Т.е. функцией распределения (вероятностей)
случайной величины X называют функцию
F(x), значение которой в точке x равно
вероятности события ![]() ,
т.е. события, состоящего только из тех
элементарных исходов, для которых
,
т.е. события, состоящего только из тех
элементарных исходов, для которых ![]() .
.
Свойства
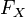 непрерывна справа:[1]
непрерывна справа:[1]
![]()
не убывает на всей числовой прямой.
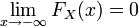 .
. .
.
Распределение случайной величины однозначно определяет функцию распределения.
Верно и обратное: если функция
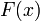 удовлетворяет
четырём перечисленным выше свойствам,
то существует вероятностное пространство
и определённая на нём случайная
величина, такая что
является
её функцией распределения.
удовлетворяет
четырём перечисленным выше свойствам,
то существует вероятностное пространство
и определённая на нём случайная
величина, такая что
является
её функцией распределения.
По определению непрерывности справа, функция имеет правый предел
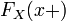 в
любой точке
в
любой точке 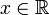 ,
и он совпадает со значением функции
,
и он совпадает со значением функции 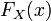 в
этой точке.
в
этой точке.В силу неубывания, функция также имеет и левый предел
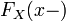 в
любой точке
,
который может не совпадать со значением
функции. Таким образом, функция
либо
непрерывна в точке, либо имеет в
ней разрыв
первого рода.
в
любой точке
,
который может не совпадать со значением
функции. Таким образом, функция
либо
непрерывна в точке, либо имеет в
ней разрыв
первого рода.
Дифференциальная функция распределения непрерывной случайной величины и ее свойства.
Числовые характеристики случайных величин.
Математическое ожидание. Математическим ожиданием дискретной случайной величины Х , принимающей конечное число значений хi с вероятностями рi , называется сумма:
![]()
Математическим ожиданием непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f(x):
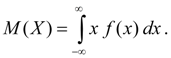
Математическое ожидание характеризует среднее значение случайной величины Х. Его размерность совпадает с размерностью случайной величины.
Свойства математического ожидания:

Дисперсия. Дисперсией случайной величины Х называется число:
![]()
Дисперсия является характеристикой рассеяния значений случайной величины Х относительно ее среднего значения М ( Х ). Размерность дисперсии равна размерности случайной величины в квадрате. Исходя из определений дисперсии (8) и математического ожидания (5) для дискретной случайной величины и (6) для непрерывной случайной величины получим аналогичные выражения для дисперсии:
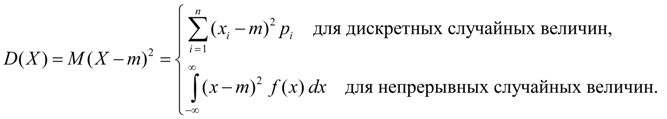
Здесь m = М ( Х ).
Свойства дисперсии:
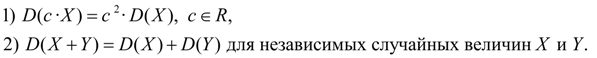 Среднее
квадратичное отклонение:
Среднее
квадратичное отклонение:
![]()
Так как размерность среднего квадратичного отклонения та же, что и у случайной величины, оно чаще, чем дисперсия, используется как мера рассеяния.
Моменты распределения. Понятия математического ожидания и дисперсии являются частными случаями более общего понятия для числовых характеристик случайных величин – моментов распределения. Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. Так, моментом порядка k относительно точки х0называется математическое ожидание М ( Х – х0)k . Моменты относительно начала координат х = 0 называются начальными моментамии обозначаются:
![]()
Начальный момент первого порядка есть центр распределения рассматриваемой случайной величины:
![]()
Моменты относительно центра распределения х = m называются центральными моментами и обозначаются:
![]()
Центральные моменты не зависят от начала отсчета значений случайной величины, так как при сдвиге на постоянное значение С ее центр распределения сдвигается на то же значение С, а отклонение от центра не меняется: Х – m = (Х – С) – (m – С). Теперь очевидно, что дисперсия – это центральный момент второго порядка:
![]()
Асимметрия. Центральный момент третьего порядка:
![]()
служит для оценки асимметрии распределения. Если распределение симметрично относительно точки х = m, то центральный момент третьего порядка будет равен нулю (как и все центральные моменты нечетных порядков). Поэтому, если центральный момент третьего порядка отличен от нуля, то распределение не может быть симметричным. Величину асимметрии оценивают с помощью безразмерногокоэффициента асимметрии:
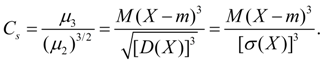
Знак коэффициента асимметрии (18) указывает на правостороннюю или левостороннюю асимметрию (рис. 2).
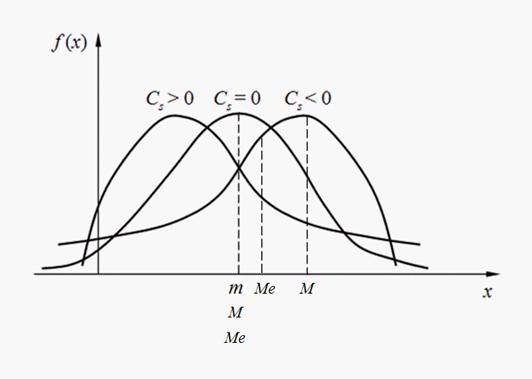 Рис.
2. Виды асимметрии распределений.
Рис.
2. Виды асимметрии распределений.
Эксцесс. Центральный момент четвертого порядка:
![]()
служит
для оценки так называемого эксцесса,
определяющего степень крутости
(островершинности) кривой распределения
вблизи центра распределения по отношению
к кривой нормального распределения.
Так как для нормального распределения![]() ,
то в качестве эксцесса принимается
величина:
,
то в качестве эксцесса принимается
величина:
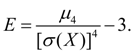
На рис. 3 приведены примеры кривых распределения с различными значениями эксцесса. Для нормального распределения Е = 0. Кривые, более островершинные, чем нормальная, имеют положительный эксцесс, более плосковершинные – отрицательный.
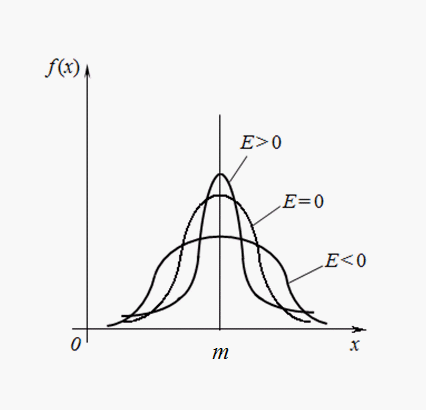 Рис.
3. Кривые распределения с различной
степенью крутости (эксцессом).
Рис.
3. Кривые распределения с различной
степенью крутости (эксцессом).
Моменты более высоких порядков в инженерных приложениях математической статистики обычно не применяются.
Мода дискретной случайной величины – это ее наиболее вероятное значение. Модой непрерывной случайной величиныназывается ее значение, при котором плотность вероятности максимальна (рис. 2). Если кривая распределения имеет один максимум, то распределение называется унимодальным. Если кривая распределения имеет более одного максимума, то распределение называетсяполимодальным. Иногда встречаются распределения, кривые которых имеют не максимум, а минимум. Такие распределения называютсяантимодальными. В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, длямодального, т.е. имеющего моду, симметричного распределения и при условии, что существует математическое ожидание, последнее совпадает с модой и центром симметрии распределения.
Медиана случайной
величины Х –
это ее значение Ме ,
для которого имеет место равенство: ![]() т.е.
равновероятно, что случайная
величина Х окажется
меньше или больше Ме.
Геометрически медиана –
это абсцисса точки, в которой площадь
под кривой распределения делится пополам
(рис. 2). В случае симметричного
модального распределения медиана, мода
и математическое ожидание совпадают.
т.е.
равновероятно, что случайная
величина Х окажется
меньше или больше Ме.
Геометрически медиана –
это абсцисса точки, в которой площадь
под кривой распределения делится пополам
(рис. 2). В случае симметричного
модального распределения медиана, мода
и математическое ожидание совпадают.
Математическое ожидание случайной величины и его свойства.
выше
Дисперсия случайной величины и ее свойства.
выше
Простейшие законы распределения дискретной случайной величины.
Название закона рас-пределения |
Краткое обозначение закона |
Обозначение случайной величины, механизм её формирования и обозначения параметров закона |
Формула закона распределения |
Выражение математического ожидания и дисперсии через параметры закона |
|
альтер-нативный |
|
|
|
|
|
биноми- альный |
|
|
|
|
|
геометри- ческий |
|
- число испытаний Бернулли, которые придётся произвести до первого успеха |
|
|
|
Пуассона |
|
1.
-
число успехов в
испытаниях
Бернулли с вероятностью
успеха
в единичном испытании, когда
велико
(несколько десятков или более), а |
|
|
|
|
2.
-
число наступлений события простейшего
потока с интенсивностью |
|
|
||
Равномерный закон распределения непрерывной случайной величины.
Показательное распределение непрерывной случайной величины.
Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Нормальный закон распределения. Кривая Гаусса.
Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности
Нормальный закон распределения также называется законом Гаусса.
Вероятность попадания нормально распределенной случайной величины в заданный интервал.
Вероятность отклонения по абсолютной величине нормально распределенной случайной величины от ее математического ожидания.
Правило трех сигм. В теории вероятностей квадратичное отклонение σx случайной величины x (от ее математического ожидания) определяется как квадратный корень из дисперсии Dx и называют также стандартным отклонением величины x
Правило
трёх сигм (![]() ) —
практически все значения нормально
распределённой случайной
величины лежат в интервале
) —
практически все значения нормально
распределённой случайной
величины лежат в интервале ![]() .
Более строго — не менее чем с 99,7 %
достоверностью значение нормально
распределенной случайной
величины лежит в указанном интервале
(при условии, что величина
.
Более строго — не менее чем с 99,7 %
достоверностью значение нормально
распределенной случайной
величины лежит в указанном интервале
(при условии, что величина ![]() истинная,
а не полученная в результате обработки
выборки).
истинная,
а не полученная в результате обработки
выборки).
Если
же истинная величина
неизвестна,
то следует пользоваться не ![]() ,
а s. Таким образом, правило трёх сигм
преобразуется в правило трёх s.
,
а s. Таким образом, правило трёх сигм
преобразуется в правило трёх s.
Вероятность отклонения относительной частоты от вероятности.
Понятие о законе больших чисел в форме Бернулли, Чебышева.
Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли - простейшим.
В
основе доказательства теорем, объединенных
термином "закон больших чисел",
лежит неравенство Чебышева, по которому
устанавливается вероятность отклонения ![]() от
ее математического ожидания:
от
ее математического ожидания:
![]()
Центральная предельная теорема Ляпунова.
Ц.П.Т. Ляпунова
Пусть
выполнены базовые предположения Ц.П.Т.
Линдеберга. Пусть случайные величины ![]() имеют
конечный третий
момент. Тогда определена
последовательность
имеют
конечный третий
момент. Тогда определена
последовательность
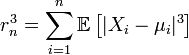 .
Если предел
.
Если предел
![]() (условие
Ляпунова),
(условие
Ляпунова),
то
![]() по
распределению при
по
распределению при ![]() .
.
Основные понятия и задачи математической статистики.
Математи́ческая стати́стика — наука, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов.
Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надёжность и точность выводов, делаемых на основании ограниченного статистического материала (напр., оценить необходимый объём выборки для получения результатов требуемой точности при выборочном обследовании).
Понятие выборки, вариационного ряда.
Выборка – набор объектов, случайно отобранных из генеральной совокупности.
Объем генеральной совокупности N и объем выборки n – число объектов в рассматривае-мой совокупности.
Виды выборки:
Повторная – каждый отобранный объект перед выбором следующего возвращается в генеральную совокупность;
Бесповторная – отобранный объект в генеральную совокупность не возвращается.
Вариационный ряд — упорядоченная по величине последовательность выборочных значений наблюдаемой случайной величины
![]()
Способы задания вариационных рядов. Примеры.
Построение вариационного ряда.
Числовые характеристики статистического распределения. Метод их расчета переходом к условным вариантам.
Эмпирическая функция распределения. Ее свойства.
Эмпирическая функция распределения (выборочная функция распределения) — естественное приближение теоретической функции распределения данной случайной величины, построенное по выборке.
Из определения функции![]() вытекают
следующие ее свойства:
вытекают
следующие ее свойства:
1) значения эмпирической функции
принадлежат отрезку ![]()
![]() ;
;
2) – неубывающая функция;
3) если ![]() –
наименьшая варианта, то
–
наименьшая варианта, то ![]() ,
при
,
при ![]() ;
;
если ![]() –
наибольшая варианта, то
–
наибольшая варианта, то ![]() при
при ![]() .
.
Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.
Понятие об эмпирических моментах вариационного ряда. Асимметрия. Эксцесс.
выше
Понятие статистических оценок параметров распределения.
Точечная оценка и ее свойства.
То́чечная оце́нка в математической статистике — это число, вычисляемое на основе наблюдений, предположительно близкое к оцениваемому параметру.
Определение
Пусть ![]() —
случайная выборка из распределения,
зависящего от параметра
—
случайная выборка из распределения,
зависящего от параметра ![]() .
Тогда статистику
.
Тогда статистику ![]() ,
принимающую значения в
,
принимающую значения в ![]() ,
называют точечной оценкой параметра
,
называют точечной оценкой параметра ![]()
Замечание
Формально
статистика ![]() может
не иметь ничего общего с интересующим
нас значением параметра
.
Её полезность для получения практически
приемлемых оценок вытекает из
дополнительных свойств, которыми она
обладает или не обладает.
может
не иметь ничего общего с интересующим
нас значением параметра
.
Её полезность для получения практически
приемлемых оценок вытекает из
дополнительных свойств, которыми она
обладает или не обладает.
Свойства точечных оценок
Оценка
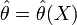 называется несмещённой,
если её математическое ожидание равно
оцениваемому параметру генеральной
совокупности:
называется несмещённой,
если её математическое ожидание равно
оцениваемому параметру генеральной
совокупности:
![]() ,
,
где ![]() обозначает математическое
ожидание в предположении,
что
—
истинное значение параметра (распределения
выборки
).
обозначает математическое
ожидание в предположении,
что
—
истинное значение параметра (распределения
выборки
).
Оценка называется эффективной, если она обладает минимальной дисперсией среди всех возможных несмещенных точечных оценок.
Оценка
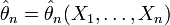 называется состоятельной,
если она по вероятности с увеличением
объема выборки n стремится к параметру
генеральной совокупности:
называется состоятельной,
если она по вероятности с увеличением
объема выборки n стремится к параметру
генеральной совокупности: 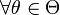 ,
,
![]() по
вероятности при
.
по
вероятности при
.
Оценка
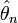 называется сильно
состоятельной, если
,
называется сильно
состоятельной, если
,
почти наверное при .
Интервальные оценки статистических параметров распределения.
Интервальной называют оценку, которая определяется двумя числами – концами интервала.
Допустим, что для изучения некоторой случайной величины X (признака генеральной совокупности) необходимо по статистическим данным произвести оценку неизвестного ее параметра θ (это может быть М(Х), D(Х) или р) с определенной степенью точности и надежности, т. е. надо указать границы, в которых практически достоверно лежит этот неизвестный параметр θ.
Это означает, что надо найти такую
выборочную оценку ![]() для
искомого параметра θ, при которой
с наибольшей вероятностью (надежностью)
будет выполняться неравенство:
для
искомого параметра θ, при которой
с наибольшей вероятностью (надежностью)
будет выполняться неравенство:
![]()
Отсюда видно, что чем меньше , тем точнее характеризуется неизвестный параметр θ с помощью выборочной оценки . Следовательно, число характеризует точность оценки параметра θ.
Точечные оценки статистических параметров распределения.
Точечной оценкой характеристики θ
называют некоторую функцию ![]() результатов
наблюдений, значения которой близки к
неизвестной характеристике θ генеральной
совокупности.
результатов
наблюдений, значения которой близки к
неизвестной характеристике θ генеральной
совокупности.
Для построения оценки нужны критерии, по которым судят о её качестве. Сформулируем некоторые свойства, позволяющие разумным образом выбирать оценки.
1. Оценка называется несмещенной, если её математическое ожидание равно оцениваемой характеристике случайной величины:
![]() ,
(1.1)
,
(1.1)
т. е. если она не дает систематической ошибки.
2. Оценка называется состоятельной,
если при увеличении числа наблюдений
оценка сходится по вероятности к искомой
величине, т. е. для любого сколь угодно
малого ![]()
![]() .
(1.2)
.
(1.2)
Если известно, что оценка несмещенная,
то для проверки состоятельности её
удобно пользоваться условием: ![]() . Если
последнее условие выполнено, то из
неравенства Чебышева следует, что оценка
состоятельная.
. Если
последнее условие выполнено, то из
неравенства Чебышева следует, что оценка
состоятельная.  .
.
Иными словами, состоятельность означает,
что оценка, построенная по большому
числу наблюдений, имеет меньший разброс
(дисперсию), т. е. ![]() .
.
Желательно иметь оценки, которые имеют наименьшую дисперсию среди всех оценок, построенных по n наблюдениям. Такие оценки называют эффективными.
Понятие корреляционной зависимости.
Корреля́ция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.
Основные задачи корреляционного анализа.
Данный метод обработки статистических данных весьма популярен в экономике и социальных науках (в частности в психологии и социологии), хотя сфера применения коэффициентов корреляции обширна: контроль качества промышленной продукции, металловедение, агрохимия, гидробиология, биометрия и прочие. В различных прикладных отраслях приняты разные границы интервалов для оценки тесноты и значимости связи.
Популярность метода обусловлена двумя моментами: коэффициенты корреляции относительно просты в подсчете, их применение не требует специальной математической подготовки. В сочетании с простотой интерпретации, простота применения коэффициента привела к его широкому распространению в сфере анализа статистических данных.
Определение параметров уравнений прямолинейного тренда МНК.
Коэффициент корреляции.
Коэффицие́нт корреля́ции или парный коэффицие́нт корреля́ции в теории вероятностей и статистике— это мера линейной зависимости двух случайных величин.
Пусть X,Y — две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:
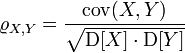 ,
,
где cov обозначает ковариацию, а D —дисперсию, или, что то же самое,
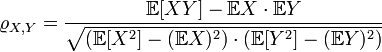 ,
,
где
символ ![]() обозначает математическое
ожидание.
обозначает математическое
ожидание.
Понятие о статистических гипотезах. Критерий согласия Пирсона.
Статистическая гипотеза представляет собой некоторое предположение о законе распределения случайной величины или о параметрах этого закона, формулируемое на основе выборки .
Критерий Пирсона, или критерий χ² (Хи-квадрат) — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.
Обозначим
через X исследуемую случайную
величину. Пусть
требуется проверить
гипотезу
![]() о
том, что эта случайная величина подчиняется
закону распределения
.
Для проверки гипотезы произведём
выборку, состоящую из n независимых
наблюдений над случайной величиной X.
По выборке можно построить эмпирическое
распределение
о
том, что эта случайная величина подчиняется
закону распределения
.
Для проверки гипотезы произведём
выборку, состоящую из n независимых
наблюдений над случайной величиной X.
По выборке можно построить эмпирическое
распределение ![]() исследуемой
случайной величины. Сравнение эмпирического
распределения
и
теоретического (или, точнее было бы
сказать, гипотетического — то есть
соответствующего гипотезе
)
распределения
производится
с помощью специального правила — критерия
согласия. Одним из таких
критериев и является критерий Пирсона.
исследуемой
случайной величины. Сравнение эмпирического
распределения
и
теоретического (или, точнее было бы
сказать, гипотетического — то есть
соответствующего гипотезе
)
распределения
производится
с помощью специального правила — критерия
согласия. Одним из таких
критериев и является критерий Пирсона.
Для проверки критерия вводится статистика:
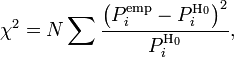
где 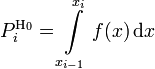 —
предполагаемая вероятность попадения
в
—
предполагаемая вероятность попадения
в ![]() -й
интервал,
-й
интервал, ![]() —
соответствующее эмпирическое значение,
—
соответствующее эмпирическое значение, ![]() —
число элементов выборки из
-го
интервала,
—
число элементов выборки из
-го
интервала, ![]() —
полный объём выборки. Также используется
расчет критерия по частоте, тогда:
—
полный объём выборки. Также используется
расчет критерия по частоте, тогда:
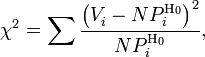
где ![]() —
частота попадания значений в интервал.
Эта величина, в свою очередь,
является случайной (в
силу случайности
)
и должна подчиняться распределению
—
частота попадания значений в интервал.
Эта величина, в свою очередь,
является случайной (в
силу случайности
)
и должна подчиняться распределению
![]() .
.