12.Системи лінійних алгебраїчних рівнянь та методи їх розв′язування

Основні поняття та означення.

Теореми Кронекера-Капеллі

1 ⁰. Лінійним рівнянням з п невідомими називається рівнян­ня вигляду

а₁х₁ + а₂х₂ + ... + а_пх_п = b,

де а₁, а_г, ..., а_п b - деякі дійсні числа, х₁, х₂, .., х_п - невідомі.

Система т лінійних рівнянь з п невідомими має такий ви­гляд:

а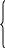 ₁₁х₁ + а₁₂х₂ + ... + а_1nх_п = b₁,

а₂₁х₁ + а₂₂х₂ + ... + а_2nх_п = b₂,

………………………….

а_m1х₁ + а_m2х₂ + ... + а_mnх_п = b_m,

де а_ij (і = 1,m, j = 1,n) - коефіцієнти при невідомих;

x_j (j = 1,n) - невідомі; b_i (і = 1,m) - вільні члени.

2 ⁰. Визначником системи називається визначник матриці, складеної з коефіцієнтів при невідомих: ∆ =

3⁰. Розв'язком системи називається сукупність значень не­відомих, які перетворюють кожне з рівнянь системи у рівність.

4⁰. Система рівнянь називається сумісною, якщо вона має принаймні один розв'язок, і несумісною, якщо вона не має розв'язків.

5⁰. Сумісна система рівнянь називається визначеною, якщо вона має єдиний розв'язок, і невизначеною, якщо має більше ніж один розв'язок.

6⁰. Якщо всі вільні члени системи дорівнюють нулю, то сис­тема називається однорідною, в іншому випадку - неоднорід­ною.

7 ⁰. Основною матрицею системи називають матрицю, складену з коефіцієнтів при невідомих: А = .

8⁰. Розширеною матрицею системи називають матрицю, яка складена з коефіцієнтів при невідомих та стовпця вільних членів.

А₁ =

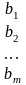
Теорема 1 (Кронекера-Капелі) Для того, щоб система лінійних рівнянь була сумісною, необхідно і досить, щоб ранги її основної та розширеної матриці були рівні.

Теорема 2 (критерій визначеності) Якщо система лінійних рівнянь з п невідомими сумісна і ранг її основної матриці дорівнює r, то

при r =n система визначена;

при r<n – невизначена.

2. Метод Крамера розв'язування систем лінійних рівнянь

Нехай система п лінійних рівнянь з п невідомими має вигляд

а ₁₁х₁ + а₁₂х₂ + ... + а_1nх_п = b₁,

а₂₁х₁ + а₂₂х₂ + ... + а_2nх_п = b₂,

………………………….

а_п1х₁ + а_п2х₂ + ... + а_пnх_п = b_п,

Теорема. Якщо визначник системи лінійних алгебраїч­них рівнянь відмінний від нуля, то ця система має єдиний розв'язок.

Р озв'язок системи можна знайти за формулами Крамера:

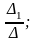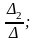х₁= х₂= …; х_п=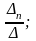

де ∆ - визначник системи,

∆_k (k є 1,п) - визначник, утворений з визначника системи заміною стовпця коефіцієнтів при шуканій змінній стовпцем вільних членів.

3. Матричний метод розв'язування систем лінійних рівнянь

Розглянемо систему п лінійних рівнянь з п невідомими:

а ₁₁х₁ + а₁₂х₂ + ... + а_1nх_п = b₁,

а₂₁х₁ + а₂₂х₂ + ... + а_2nх_п = b₂,

………………………….

а_п1х₁ + а_п2х₂ + ... + а_пnх_п = b_п,

Позначимо через A - матрицю, складену із коефіцієнтів при невідомих (так звану основну матрицю системи);

X - матрицю-стовпець із невідомих;

В - матрицю-стовпець з вільних членів, тобто

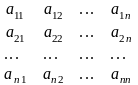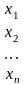А = , X = , B =

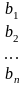
Тоді систему рівнянь можна переписати у вигляді матричного рівняння: АХ = B.

X = A^-1B - матричний розв'язок системи лінійних рівнянь.

Знаходження матричного розв'язку називається матрич­ним способом розв'язування систем лінійних рівнянь.