1.3. Электрон-ядерное взаимодействие и сверхтонкая структура спектра эпр

Если неспаренный электрон находится вблизи ядра со спином I  0, то в результате взаимодействия их магнитных моментов происходит расщепление зеемановских уровней энергии электрона. Зависимость энергии уровней от поля в этом случае несколько усложняется:

, (11)

где – константа сверхтонкого взаимодействия (СТВ), m_I - магнитное квантовое число проекции ядерного спина на ось , вдоль которой направлено магнитное поле.

При взаимодействии электрона с одним ядром, спин которого I=½, каждый из электронных уровней расщепляется на два (рис.3).

Рис. 3. Схема расщепления электронных зеемановских уровней (H=const) при взаимодействии с ядерным спином I = ½. Стрелками показаны переходы, индуцируемые микроволновым излучением.

В соответствии с правилами отбора m_s = 1 и m_I = 0 возможны два индуцированных микроволновым излучением перехода:

(12)

Так, например, для атомов водорода в твердотельной матрице при взаимодействии электрона с протоном в спектре ЭПР наблюдается не один пик, а дублет с центром при g = 2.0023. При этом, поскольку площадь под кривой поглощения ЭПР не зависит от величины спина ядра, при расщеплении одиночной линии ЭПР на две или несколько компонент интенсивность каждой компоненты будет соответственно в два или несколько раз ниже. В общем случае взаимодействия электрона с ядром со спином I число линий в спектре ЭПР будет равно 2I+1.

При взаимодействии неспаренного электрона с двумя ядрами энергии уровней будут зависеть от двух ядерных квантовых чисел m₁ и m₂ :

, (13)

где – константы СТВ с первым и вторым ядром соответственно. С учетом правил отбора (см. выше) для энергии разрешенных переходов получим:

, (14)

Отметим, что константы СТВ можно выразить и в единицах измерения поля H , если поделить их величины на произведение g_B. При развертке спектра по магнитному полю при условии =const и, обозначая для неспаренного электрона резонансное значение поля H₀, для резонансных линий взаимодействующего с ядрами электрона получим:

, (15)

или в общем случае n ядер:

, (16)

Таким образом, при взаимодействии электрона с несколькими ядрами общую картину спектра ЭПР можно представить следующим образом. Вначале линия ЭПР расщепляется от наиболее сильного взаимодействия с одним из ядер, затем каждая из компонент спектра расщепляется от взаимодействия со следующим ядром и т.д.

Для двух одинаковых ядер, например, протонов это показано на рис. 4а.

Рис. 4 а. Расщепление линий в спектре ЭПР при взаимодействии электрона с двумя эквивалентными ядрами. Энергетические уровни и переходы изображены для случая H = const.

Рис. 4 б. Спектр ЭПР анион-радикала бензола.

Отметим, что двукратное вырождение уровней (m_I = 0) обусловлено двумя возможными перестановками спинов (рис. 4а). Как следствие этого, относительные интенсивности разрешенных переходов распределяются в отношении 1:2:1. В общем случае, при наличии n эквивалентных ядер со спином I, взаимодействующих с электроном, мультиплетность сигнала ЭПР равна (2nI+1). В случае, когда I=½, отношение интенсивностей компонент мультиплета такое же, как отношение коэффициентов биномиального разложения (x+1)ⁿ (см. треугольник Паскаля в [1]). Например, спектр ЭПР анион-радикала бензола представляет собой септет с константой =3.75 Гс и соотношением интенсивностей компонент 1:6:15:20:15:6:1 (рис. 4б). В данном радикале электрон делокализован по бензольному кольцу и одинаково взаимодействует со всеми шестью протонами. При взаимодействии электрона с несколькими наборами эквивалентных ядер со спинами I_i число линий в спектре ЭПР будет равно произведению:

(17)

Величина константы СТВ, т.е. расстояние между линиями в мультиплетах, зависит от электронной спиновой плотности на ядре. Следует подчеркнуть, что спиновая плотность – это не то же самое, что плотность неспаренного электрона (хотя в простейших случаях они могут и совпадать). Дело в том, что орбиталь неспаренного электрона может поляризовать спины спаренных электронов на прилежащей связи, т.е. каждый из них будет несколько ближе к одному из связанных ядер, чем к другому. Следовательно, на каждом из ядер будет некоторая спиновая плотность, даже на том, где нет плотности неспаренного электрона.

В общем случае, как и g – фактор, константа СТВ – величина тензорная. Для изотропных систем этот тензор характеризуется одним параметром (сферическая симметрия), а для анизотропных систем имеет два или три независимых параметра. Анизотропия СТВ обусловлена взаимодействием между электронным и ядерным магнитными диполями. Гамильтониан такого диполь – дипольного взаимодействия имеет следующий вид:

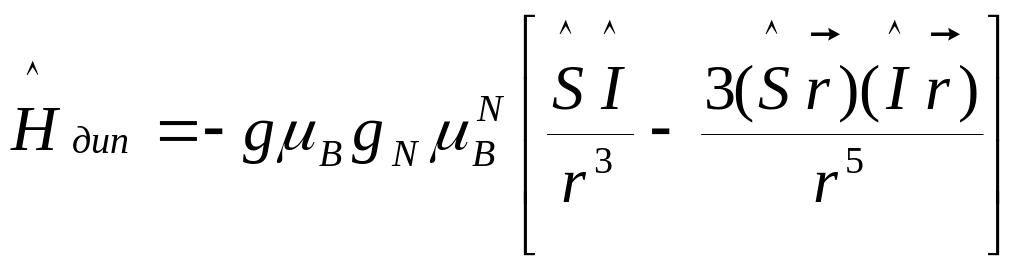, (18)

где и - ядерный - фактор и магнетон Бора, соответственно,

и - операторы спина электрона и ядра, соответственно,

- вектор, соединяющий электрон и ядро.

Часто анизотропия тензора СТВ настолько усложняет спектры ЭПР, что для их анализа и правильной интерпретации требуется компьютерная обработка. Более подробно ознакомиться с анизотропией СТВ можно, например, в книге [1].