
- •Оглавление
- •Введение
- •§1. Введение в теорию эпр
- •1.1. Условие электронного парамагнитного резонанса
- •1.3. Электрон-ядерное взаимодействие и сверхтонкая структура спектра эпр
- •1.4. Интенсивность и форма линии в спектре эпр. Времена релаксации системы спинов
- •§2. Техника эпр-спектроскопии
- •2.1. Принцип устройства эпр-спектрометра
- •2.2. Основные параметры и узлы эпр-спектрометра ps100.X
- •2.3. Программа для измерения спектров эпр. Общие рекомендации по выбору параметров
- •§3. Исследование методом эпр кристаллических, неупорядоченных и низкоразмерных образцов.
- •3.2. Особенности применения метода эпр для изучения спиновых центров в неупорядоченных и низкоразмерных полупроводниках и диэлектриках
- •§ 4. Упражнения
- •4.1 Знакомство с устройством и порядком работы на эпр-спектрометре
- •4.3. Исследование спиновых центров в образцах a-Si:h и a-Si1-X Cx:h
- •Список рекомендуемой литературы:
4.3. Исследование спиновых центров в образцах a-Si:h и a-Si1-X Cx:h
В качестве объекта исследования используются образцы аморфного карбида кремния переменного состава a-Si1-xCx:H (x=00.3), полученные методом CVD в тлеющем разряде.
В данном упражнении необходимо выполнить следующие измерения.
Получить серию зависимостей для всех исследуемых пленок a-SixCx-1:H. Для этого прописать спектры ЭПР при следующих значениях мощности в децибеллах: 1, 5, 10, 15, 20, 25 и 30. Построить график
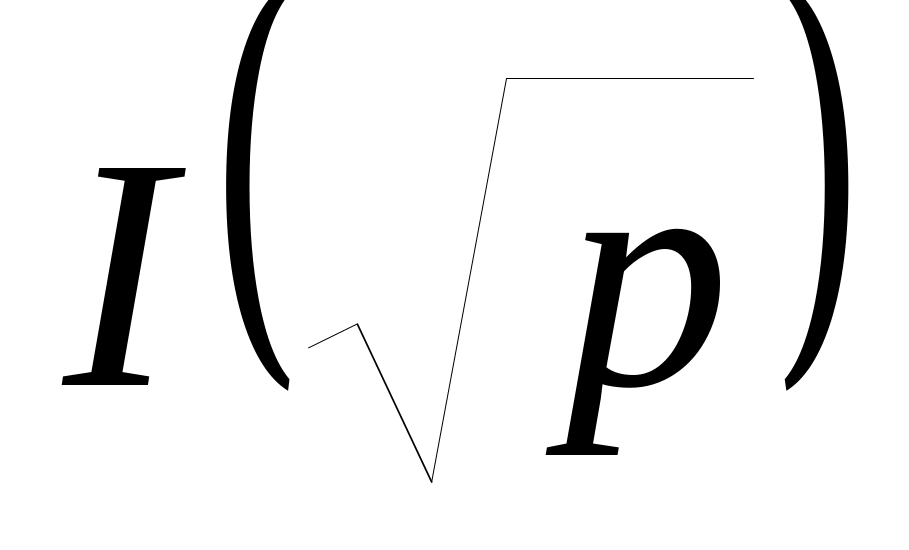 .
Определить, в каком интервале значений
микроволновой мощности отсутствует
насыщение для каждого из образцов.
.
Определить, в каком интервале значений
микроволновой мощности отсутствует
насыщение для каждого из образцов.Положив в ампулу с a-SixCx-1:H
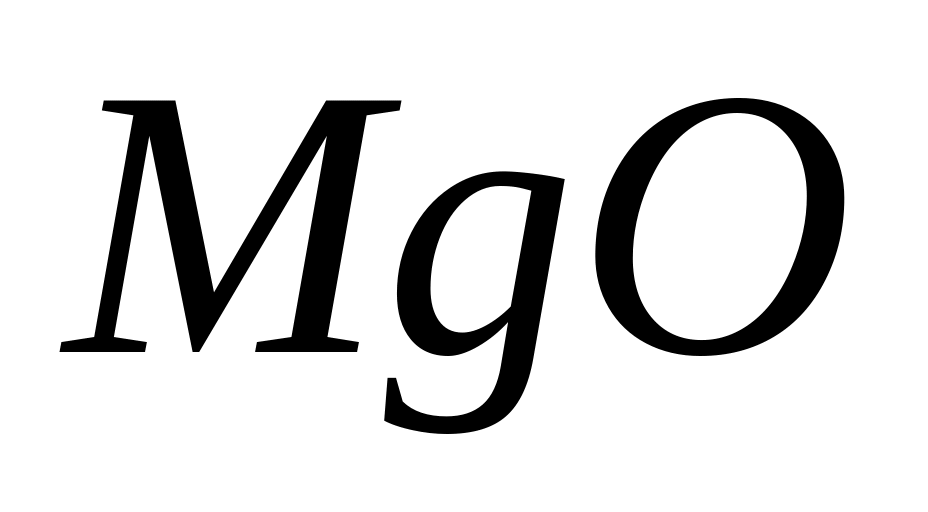 с
с
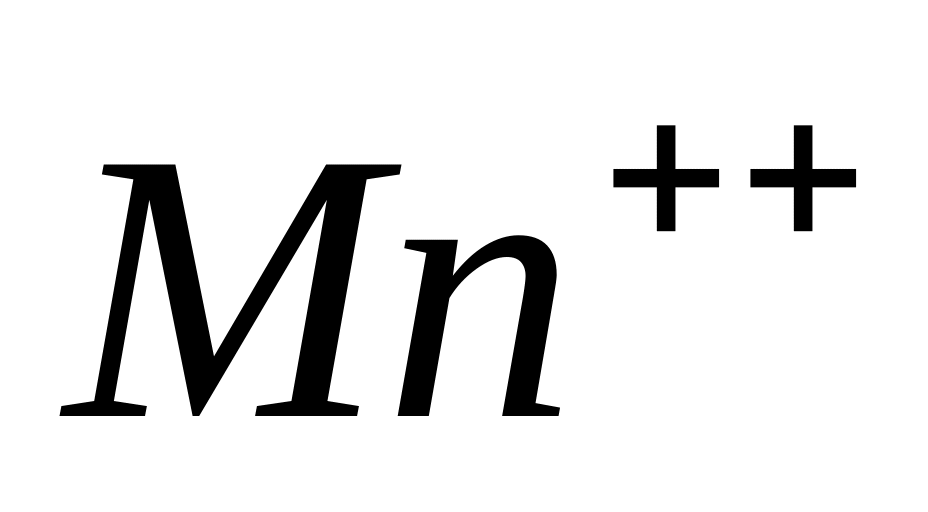 и выбрав значение P,
при котором сигнал ЭПР не насыщается
ни для одного из образцов, прописать
спектры ЭПР для всех исследуемых
образцов.
и выбрав значение P,
при котором сигнал ЭПР не насыщается
ни для одного из образцов, прописать
спектры ЭПР для всех исследуемых
образцов.Получить спектр ЭПР эталона концентраций . При этом следует учесть, что параметры спектра ЭПР для эталона и условия эксперимента (месторасположение образца в резонаторе и температура измерения) должны быть выбраны по возможности такими же, как и для исследуемого образца. Если какие-либо параметры спектра ЭПР не удается выбрать одинаковыми, необходимо произвести перерасчет данных эксперимента, умножив или разделив спектр эталона на соответствующие коэффициенты. Отметим, что интенсивность линии в спектре ЭПР во всем диапазоне значений зависит линейно от амплитуды модуляции, коэффициента усиления и корня из микроволновой мощности (в отсутствие насыщения).
По спектрам, полученным в п.п. 2, и 3 определить следующие параметры: 1) ширину линии ЭПР, 2) g-фактор (используя сигнал от ионов Mn++, рассчитать по формуле (34)), 3) концентрацию дефектов.
Примечания:
Методика расчета концентрации спиновых центров приведена в Приложении.
Абсолютная концентрация спинов в эталонном образце составляет (6.00.2)*1018.
4.4. ЭПР-спектроскопия пористого кремния
В работе исследуются пленки пористого кремния, окисленные химически, например, путем выдержки образцов в парах NO2.
Порядок выполнения упражнения.
Получить серию зависимостей для окисленного пористого кремния в вакууме. Для этого прописать спектры ЭПР при следующих значениях микроволновой мощности в децибеллах: 2, 5, 10, 15, 20 и 25. Построить график . Определить, в каком интервале значений микроволновой мощности отсутствует насыщение.
Положив в ампулу с исследуемым образцом с и выбрав значение Р, при котором сигнал ЭПР не насыщается, прописать спектр ЭПР.
Выбрав значение Р, при котором сигнал ЭПР не насыщается, прописать спектр ЭПР при различных ориентациях поверхности пленки и направления магнитного поля:
H поверхности пленки пористого Si;
H составляет угол 450 с поверхностью пленки пористого Si;
H поверхности пленки пористого Si.
Прописать спектр ЭПР с учетом рекомендаций упражнения 4.3.
По полученным спектрам ЭПР определить g-фактор, ширину линии и концентрацию спиновых центров (см. п.4.2 и Приложение).
Приложение. Методика расчета концентрации спиновых центров
В качестве примера
рассмотрим расчет концентрации спиновых
центров в образце с использованием
стандартной графической программы
“Origin”. Аналогичные рассуждения
справедливы для любой другой программы
как стандартной, так и написанной
самостоятельно. Используя рекомендации
п.2.3, экспериментальные данные
представляются в виде таблицы из двух
столбцов A(x) (магнитное поле) и B(y)
(интенсивность сигнала ЭПР) и/или
графически. Для расчета нам потребуется
два спектра: от эталонного образца
CuCl2·2H2O
и от исследуемого (например, окисленного
пористого кремния). Начнем с эталона.
Сначала необходимо проверить, совпадает
ли уровень шума в спектре с нулевым
уровнем. Если нет, измерить курсором
величину, на которую сдвинут спектр ЭПР
по отношению к нулевой линии y
= 0, и вычесть
ее из столбца B(y), предварительно выделив
его и используя операцию Set
Column Values.
Затем
добавить в таблицу данных еще один
столбец C(y) (для этого воспользоваться
правой клавишей мыши и операцией Add
New Column).
Скопировать в него содержимое столбца
B(y). После этого, используя опять операцию
Set Column Values,
задать в командной строке операцию
интегрирования:
![]() .
Причем нумерация порядкового индекса
i
должна начинаться с двух (i
= 2...4096). В
результате интегрирования первой
производной линии поглощения (столбец
B(y)), мы получим саму кривую поглощения
ЭПР (столбец C(y)). Далее, задав курсором
начало и конец интегрирования на графике,
осью х которого является столбец A(x), а
осью y столбец C(y), и выбрав операцию
интегрирования в строке меню
Analysis/Calculus/Integrate,
получим численное значение Sэт,
представляющее собой площадь под кривой
поглощения эталонного образца. Аналогичную
операцию необходимо проделать со
столбцами данных исследуемого образца.
В результате получим численное значение
Sx
площади под кривой поглощения исследуемого
образца. Далее, используя очевидное
соотношение:
.
Причем нумерация порядкового индекса
i
должна начинаться с двух (i
= 2...4096). В
результате интегрирования первой
производной линии поглощения (столбец
B(y)), мы получим саму кривую поглощения
ЭПР (столбец C(y)). Далее, задав курсором
начало и конец интегрирования на графике,
осью х которого является столбец A(x), а
осью y столбец C(y), и выбрав операцию
интегрирования в строке меню
Analysis/Calculus/Integrate,
получим численное значение Sэт,
представляющее собой площадь под кривой
поглощения эталонного образца. Аналогичную
операцию необходимо проделать со
столбцами данных исследуемого образца.
В результате получим численное значение
Sx
площади под кривой поглощения исследуемого
образца. Далее, используя очевидное
соотношение:
![]() ,
получим выражение для абсолютной
концентрации спиновых центров исследуемого
образца :
,
получим выражение для абсолютной
концентрации спиновых центров исследуемого
образца :
![]() .
Напомним, что абсолютная концентрация
спиновых центров в эталоне составляет
.
Напомним, что абсолютная концентрация
спиновых центров в эталоне составляет
![]() .
Абсолютная концентрация спинов, как
уже отмечалось (см п.1.4), малоинформативна.
Поэтому необходимо пересчитать полученное
значение либо на единицу массы, либо на
единицу объема или площади поверхности,
т.е. Nx
будет, соответственно, равно:
.
Абсолютная концентрация спинов, как
уже отмечалось (см п.1.4), малоинформативна.
Поэтому необходимо пересчитать полученное
значение либо на единицу массы, либо на
единицу объема или площади поверхности,
т.е. Nx
будет, соответственно, равно:
![]() .
.
* * *
Авторы выражают благодарность Осминкиной Л.А. и
Силоч А.Ю. за помощь в компьютерном наборе данного учебного пособия.
