6. Постановка и математическая модель транспортной задачи.

Модель 3.Транспортная задача.Экономическая постановка.

Имеется m поставщиков и n потребителей однородной продукции. Известны удельные затраты на доставку единицы прод. от каждого поставщ. каждому потреб. Запасы прод. у поставщ. ограничены. Известны также потребности в прод. каждого потреб. Необходимо опр-ть такой план перевозки прод. от поставщиков к потребителям, при кот. общие затраты на перевозку будут минимальными.

Математическая постановка.

Введём обозначения заданных параметров:

j – индекс потребителей, j = 1,n;

i – индекс поставщиков, i = 1,m;

Аi – объём имеющейся продукции i-го поставщика;

Вj – объём потребности в продукции j-го потребителя;

cij – удельные затраты на перевозку единицы продукции от i-го поставщика j-му потребителю.

Введём неизвестные переменные:

хij – планируемый объём перевозки продукции от i-го поставщика j-му потребителю.

В терминах введённых обозначений данная задача запишется следующим образом.

z = c₁₁x₁₁ + c₁₂x₁₂ +…+ c_1nx_1n + c₂₁x₂₁ +…+ _{cm(n-1)xm (n-1)} + c_mnx_mn → min; (1) Ограничения задачи.

I. От каждого поставщика можно вывести объём продукции не более имеющегося количества:

x₁₁ + x₁₂ +…+ x_1n ≤ A₁,

x₂₁ + x₂₂ +…+ x_2n ≤ A₂, (2)

…………………….

x_m1 + x_m2 +…+ x_mn ≤ A_m.

II. Потребность каждого потребителя в продукции должна быть удовлетворена:

x₁₁ + x₂₁ +…+ x_m1 ≥ B₁,

x₁₂ + x₂₂ +…+ x_m2 ≥ B₂,

……………………. (3)

x_1n + x_2n +…+ x_mn ≥ B_n.

III. Условие неотрицательности:

xij ≥ 0, i = 1,m , j = 1,n. (4)

7. Постановка и математическая модель задачи о назначении.

Модель 4. Задача о назначениях. Эк-я постановка.

Имеются n видов работ и n исполнителей. Каждый из исполнителей может выполнить любую, но только одну работу. Задана эффективность выполнения каждой работы, каждым исполнителем. Необходимо закрепить исполнителей за работами таким образом, чтобы общая эффективность выполнения работ была максимальной.

Введём обозначения заданных параметров.

i – индекс работ, i = 1,n;

j – индекс исполнителей, j = 1,n;

ijс – эф-ность выполнения i-й работы j-м исполнителем.

Введём неизвестные переменные. В данной задаче они могут принимать только два значения - 0 или 1. Такие переменные называются булевыми.

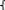1 - если за i-й работой закреплён j-й исполнитель;

xij= 0 - в противном случае.

В терминах введённых обозначений данная задача запишется следующим образом:

z=c₁₁x₁₁+c₁₂x₁₂+…+c_1nx_1n+c₂₁x₂₁+…+c_(n-1)(n-1)x_(n-1)(n-1)+ +c_nnx_nn→max;

Ограничения задачи.

I. За каждой работой должен быть закреплён только один исполнитель:

x₁₁ + x₁₂ +…+ x_1n = 1,

x₂₁ + x₂₂ +…+ x_2n = 1,

……………………..

x_n1 + x_n2 +…+ x_nn = 1.

II. Каждый исполнитель может выполнить только 1 работу:

x₁₁ + x₂₁ +…+ x_n1 = 1,

x₁₂ + x₂₂ +…+ x_n2 = 1,

……………………..

x_1n + x_2n +…+ x_nn = 1,

xij = {0,1} i = 1,n, j = 1,n