4 Дискретизация и восстановление непрерывных сигналов

Информация, содержащаяся в сигналах, может храниться, передаваться и обрабатываться как в непрерывной, так и в дискретной форме, но на современном этапе развития информационной техники предпочтение отдается дискретным сигналам.

4.1 Дискретизация и квантование непрерывных сигналов

Непрерывный (аналоговый) сигнал преобразуется в дискретный сигнал путем последовательного выполнения двух операций – дискретизации по времени и квантования по уровням.

Под дискретизацией понимают преобразование функции непрерывного времени (рисунок 1^а)) в функцию дискретного времени (рисунок 1^б)), представляемую совокупностью величин, называемых координатами, по значениям которых исходная непрерывная функция может быть восстановлена с заданной точностью. Роль координат обычно выполняют мгновенные значения функции, отсчитанные в определенные моменты времени.

Рисунок 1 – Дискретизация по времени непрерывной функции

Под квантованием понимают преобразование некоторой величины с непрерывной шкалой значений в величину, имеющую дискретную шкалу значений (рисунок 2). Оно сводится к замене любого мгновенного значения одним из конечного множества разрешенных значений, называемых уровнями квантования. Если провести нумерацию уровней квантования, то их передача сведется к передаче обычных чисел. Выразив числа в какой-либо системе счисления, можно обойтись меньшим множеством передаваемых символов. Как правило, дискретный сигнал преобразуется в последовательность чисел, выраженных в двоичном коде.

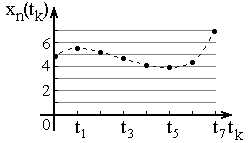
Рисунок 2 – Квантование по уровню

На рисунке 2 в качестве примера выбрано восемь (начиная с нулевого) разрешенных уровней квантования.

Для восьми уровней достаточно трех двоичных разрядов: для нулевого – 000, для первого – 001, для второго – 010, для третьего – 011, для четвертого – 100, для пятого – 101, для шестого – 110, для седьмого – 111.

Конечное выражение для двоичного кода проквантованного сигнала примет вид:

101; 101; 101; 101; 100; 100; 100; 111.

4.2 Сигналы с ограниченным спектром

При построении метода дискретизации аналогового сигнала необходимо сформулировать критерий выбора дискретных отсчетов, установить процедуру восстановления по ним исходного сигнала и иметь возможность определять возникающую при этом ошибку. Решение указанной задачи возможно лишь на базе выбора определенной математической модели дискретизируемого сигнала. Наибольшее распространение получила модель сигнала с ограниченным спектром. В этом случае величина шага дискретизации ставится в соответствие с наивысшей частотой, присутствующей в спектре сигнала.

Сигналом с ограниченным спектром называют сигнал, математическая модель которого обладает следующим свойством – спектр сигнала принимает ненулевые значения лишь в ограниченной полосе частот от нуля до граничной частоты . С физической точки зрения такая модель сигнала оправдана тем, что вклад спектральных составляющих при пренебрежимо мал в силу ограниченности энергии сигналов. Необходимо учесть и то, что любое реальное устройство, предназначенное для передачи и обработки сигналов, имеет конечную ширину полосы пропускания.

Примером сигнала с ограниченным спектром может служить идеальный низкочастотный сигнал (рисунок 3), спектральная плотность которого описывается функцией:

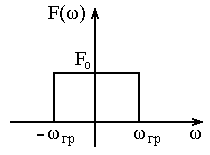
Рисунок 3 – Спектр идеального низкочастотного сигнала

Математическую модель идеального низкочастотного сигнала (ИНС) во временной области можно получить из формулы обратного преобразования Фурье:

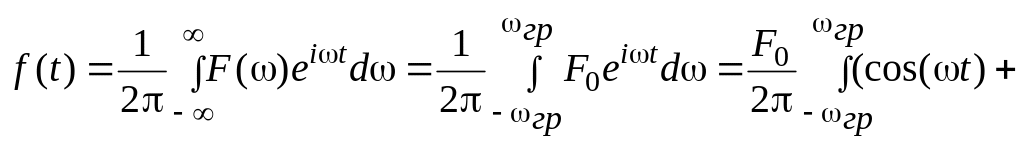
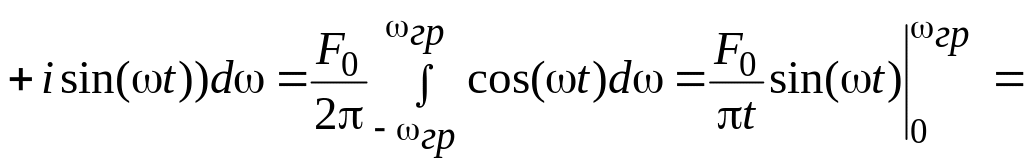
. (1)

Для построения графика функции (1) рассмотрим несколько частных случаев:

1. ;

2. ;

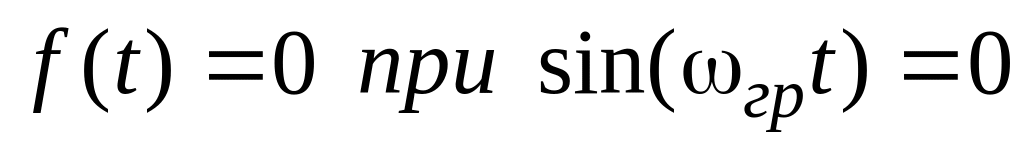3. , откуда

График ИНС (рисунок 4) имеет вид осциллирующей кривой, четной относительно начала отсчета времени. С увеличением граничной частоты спектра возрастают как центральный максимум, так и частота осцилляций.

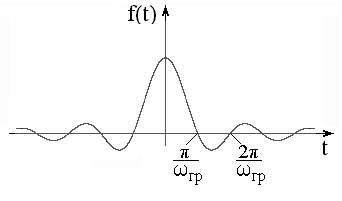
Рисунок 4 – Идеальный низкочастотный сигнал