Тема 2. Сводка и группировка данных

Группировку с равными интервалами выполняют, когда вариация признака невелика, k - количество групп. (интервал: конец – начало-конец)

• , n 30 n – объем совокупности.

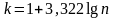, то есть n > 30

размер интервала равен:

,

2. При группировке с неравными интервалами:

- при равнонаполненных интервалах:

• , n 30 n – объем совокупности.

, то есть n > 30

• определяется количество единиц, которое должно быть в каждой группе: ;

• ранжируются единицы совокупности по возрастанию группировочного признака;

• проводится непосредственно группировка;

б) при прогрессивно возрастающих или убывающих в арифметической прогрессии интервалах величина i-того интервала:

где h - величина первого интервала: ; i - порядковый номер интервала.

Аналит.группировка:

1. х-факторный признак, у – результативный признак. Мера связи между факторным и результативным признаком

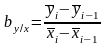
Тема 4. Статистические показатели

коэффициентах, процентах, промилле (⁰/₀₀), продецимилле (⁰/₀₀₀)

1.Относительная величина планового задания

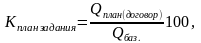
г

де Q_план и Q_баз – плановый и базисный размеры явления за период.

2. Относительная величина выполнения плана (нормы или договорных обязательств)

,

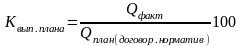где Q факт – фактический объем явления за отчетный период.

3. Относительная величина динамики

Рассмотренные относительные величины взаимосвязаны между собой: К_{динамики} = К_{план. задания} · К_{вып. плана}

4. Относительная величина структуры d = (100).

5. Относительная величина координации Показывает, сколько единиц данной части целого приходится на 1, 10, 100, 1000 и т.п. единиц части, принятой за базу сравнения:

K_{координации} = K₁ : K₂ : ... : K _баз , ,

где Q_баз– уровень, принятый за базу сравнения; Q₁+ Q ₂+...+ Q_баз=Q_целое

6. Относительная величина интенсивности

7. Относительная величина сравнения – отношение одноименных величин, относящихся к разным объектам или территориям, взятое, как правило, за одно и то же время. Выражается в коэффициентах.

Средняя величина – это обобщающий показатель, который характеризует типичный уровень варьирующего признака в расчете на единицу однородной совокупности. в общем виде формально это соотношение может быть представлено в форме агрегатной средней:

где M – объем явления или объем признака; n – объем совокуп-ности,

В статистике вычисляют следующие виды средних величин:

1. среднюю арифметическую; 4) моду и медиану;

2. среднюю гармоническую; 5) среднюю хронологическую;

3. среднюю квадратическую; 6) среднюю геометрическую.

Указанные средние величины можно объединить в две группы: степенные средние (средняя арифметическая, средняя гармоническая, средняя квадратическая и средняя геометрическая) и структурные средние (мода и медиана). Общая формула степенной средней имеет вид: ,

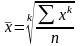где k - показатель степени средней.

При k = -1 - средняя гармоническая; k = 0 - средняя геометрическая;

k = 1 - средняя арифметическая; k = 2 - средняя квадратическая.

Признак, по которому находится средняя, называется осредняемым признаком и обозначается . Величины осредняемого признака у каждой единицы совокупности называются индивидуальными его значениями или вариантами. Обозначаются как x₁, x₂, x₃, …x_n.. Частота (повторяемость) индивидуальных значений признака – f

Каждая средняя в зависимости от характера представления исходных данных рассчитывается двумя способами – как простая и как взвешенная. Если признак не сгруппирован, то применяется форма простой средней; если признак заранее сгруппирован, то применяется форма взвешенной средней.

Средняя арифметическая простая: ,

где n – количество единиц совокупности (n = f)

Средняя арифметическая взвешенная: ,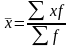

где xf = M – объем явления.

В интервальных вариационных рядах значение признаков дано в виде интервалов “от … до …”. Для расчета средней в этом случае необходимо перейти к дискретному ряду, т.е. в каждом интервале найти среднее значение (x), а затем расчет выполнять по средней арифметической взвешенной:

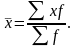
_{Средняя гармоническая} – это величина, обратная средней арифметической. Применяется, если заданы объемы явлений (объемы признаков), но не известны частоты. По способу расчета средняя гармоническая бывает:

_{- простая, применяется, когда объемы признака (n) равны.}

_{- взвешенная, применяется, когда известны индивидуальные значения признака (х), но не заданы веса (f), которые входят сомножителем в известный объемный показатель (М = х f).}

Если в условии задачи известен знаменатель исходной схемы, а неизвестен числитель, то применяется средняя арифметическая взвешенная. Если известен числитель, а знаменатель – нет, то используется средняя гармоническая взвешенная.

Средняя квадратическая применяется в тех случаях, когда варианты представляют собой отклонение заданных величин от нормы,

Рассчитывается: 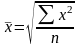- простая; - взвешенная;

где f – количество единиц совокупности с тем или иным отклонением; х – отклонения