
- •3. Частотные свойства электрических цепей. Резонансные цепи
- •3.1. Общие сведения
- •Резонанс напряжений
- •Резонанс токов
- •Резонанс в контурах с индуктивной связью
- •4. Четырехполюсники
- •Общие сведения и классификация
- •Основные уравнения пассивного четырехполюсника
- •4.3. Схемы замещения четырехполюсников
- •Решение. Определив по (4.6) параметр
- •4.4. Характеристические параметры четырехполюсников
- •Активные четырехполюсники
- •Автономные активные четырехполюсники
- •Неавтономные активные четырехполюсники
- •Четырехполюсники с интегральными операционными усилителями
- •Сопротивление , связывающее входные и выходные зажимы оу, называют сопротивлением обратной связи.
- •5. Цепи с периодическими
- •5.1. Общие сведения
- •5.2. Расчет электрической цепи с несинусоидальными сигналами
- •Особенности измерения несинусоидальных величин
- •5.4. Энергетические показатели
- •6. Трехфазные электрические цепи
- •Общие сведения
- •Симметричная трехфазная цепь
- •Несимметричная трехфазная цепь, соединенная звездой
- •Несимметричная трехфазная цепь, соединенная треугольником
- •Мощность трехфазной цепи
- •Решение. Каждый из ваттметров показывает величину
- •Порядок расчета сложной несимметричной трехфазной цепи
- •6.6. Высшие гармоники в трехфазных цепях
- •6.7. Получение вращающегося магнитного поля.
- •Литература
5.4. Энергетические показатели
Активная мощность периодического тока произвольной формы определяется как среднее значение мгновенной мощности за период основной гармоники:
![]() .
.
Подставляя u и i, согласно (5.1), в форме ряда, после интегрирования получаем:
![]() ,
Вт.
,
Вт.
(5.12)
Здесь
![]() ,
,
![]() - действующие
значения напряжения и тока
- действующие
значения напряжения и тока
k - гармоники;
![]() -
разность начальных фаз напряжения
и тока
-
разность начальных фаз напряжения
и тока
k - гармоники.
Аналогично можно записать для реактивной мощности:
![]() ,
(5.13)
,
(5.13)
где
![]() ,
вар.
,
вар.
Полная
мощность:
![]() ,
ВА. (5.14)
,
ВА. (5.14)
Мощность
искажения:
![]() ,
вар. (5.15)
,
вар. (5.15)
Для резистивной цепи Т = 0.
ПРИМЕР 5.4. Определить активную (Р) и полную (S) мощности, а также мощность искажения в электрической цепи по рис. 5.6 с известными параметрами R = 3 Ом; L = 1 мГн; С = 0,5 мФ; = 1000 рад/с при действии источника ЭДС
e(t) = 20 + 42,3 sin(t) + 30 sin(2t + 450) В.
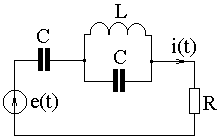
Рис. 5.6
РЕШЕНИЕ. Для определения мощностей Р, S и Т необходимо знать действующие значения гармонических составляющих входного тока и напряжения, а также их начальные фазы:
![]()
![]() ;
;
,
где
![]() - реактивная мощность.
- реактивная мощность.
В данной цепи последовательно с источником ЭДС включен емкостный элемент, поэтому ток нулевой гармоники I0 = 0.
Ток первой (основной) гармоники в комплексной форме:
![]() ,
,
где
![]() .
.
Подставляя
численные значения
![]() = L
= 1000
10-3
= 1 Ом,
= L
= 1000
10-3
= 1 Ом,
![]() Ом,
Ом,
находим
:
![]() =
3 - j
2 +
j 1
(
-
j
2
)
/
(
j
1 -
j 2
) =
3 - j 2
+ j 2 = 3 Ом
=
3 - j
2 +
j 1
(
-
j
2
)
/
(
j
1 -
j 2
) =
3 - j 2
+ j 2 = 3 Ом
и
![]() = 30/3 = 10 А.
= 30/3 = 10 А.
Для
второй гармоники :
![]() =
2 Ом,
=
2 Ом,
![]() =
1 Ом,
=
1 Ом,
![]() Ом
и, следовательно,
Ом
и, следовательно,
![]() А.
А.
Активная мощность цепи:
![]()
Реактивная мощность:
![]() вар.
вар.
Полная мощность:
![]() ВА.
ВА.
Мощность искажения:
![]() вар.
вар.
ПРИМЕР
5.5. Определить показания приборов
электромагнитной системы в цепи по
рис. 5.7, а, подключенной к источнику
напряжения
![]() В. Параметры индуктивно связанных
катушек: R
= 30 Ом; L
= 0,4 Гн;
коэффициент связи kСВ
= 0,5. Измерительные приборы считать
идеальными.
В. Параметры индуктивно связанных
катушек: R
= 30 Ом; L
= 0,4 Гн;
коэффициент связи kСВ
= 0,5. Измерительные приборы считать
идеальными.
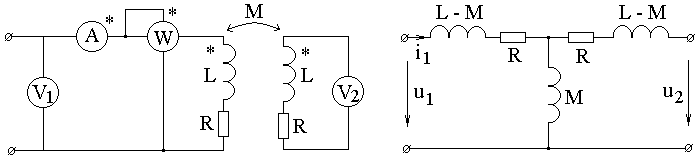
а б
Рис. 5.7
РЕШЕНИЕ. От воздействия на цепь постоянной составляющей входного напряжения имеем:
![]() А,
А,
при
этом напряжение во вторичной цепи
отсутствует:
![]() .
.
Для
основной гармоники расчет произведем,
развязав индуктивные связи, как показано
на рис. 5.7, б. Здесь М - взаимная индуктивность,
равная:
![]() Гн.
Гн.
Действующее значение тока первой гармоники в комплексной форме:
![]() А.
А.
Напряжение на выходном вольтметре (V2) определяется только напряжением ветви с взаимной индуктивностью:
![]() В.
В.
Таким образом, найденные токи и напряжения:
![]() А;
А;
![]() В.
В.
Электромагнитные приборы реагируют на действующие значения, поэтому их показания:
![]() В;
В;
![]() А;
А;
![]() В;
В;
![]()
