4.5. Синтез локально-оптимального управления
При проектировании систем управления часто бывает необходимо, чтобы поведение системы было оптимальным в некотором смысле в любой текущий момент времени.
Рассмотрим непрерывный управляемый процесс, описываемый системой дифференциальных уравнений (4.18).
Пусть задан функционал (функция)
параметрически зависящий от времени
и определенный на множестве функций
и
.
Требуется найти уравнение
,
минимизирующее
,
где
-текущий момент времени. Такое управление
называется локально-оптимальным.
В качестве критерия оптимальности рассмотрим функционал
, (4.27)
матрица
удовлетворяют тем же требованиям, что
и в параграфе 4.4.
Нетрудно показать [6], что локально-оптимальное уравнение с необходимостью удовлетворяет условию
. (4.28)
Воспользуемся этим условием.
Тогда, дифференцируя (4.27) в силу (4.18),
найдем выражение для определения
производной
(4.29)
Учитывая далее, что силу симметричности
матрицы
,
из условия
найдем локально-оптимальное управление
(4.30)
Найденное управление действительно
доставляет производной
,
так как
.
Из выражения (4.30) следует, что
локально-оптимальное управление
полностью определяется матрицами
,
а для реализации его необходима полная
информация о состоянии процесса
.
Задаваясь различными матрицами весовых
функций
,
можно обеспечить те или иные свойства
управляемого процесса, в частности
свойства устойчивости или асимптотической
устойчивости.
Потребуем, например, чтобы на локально-оптимальном управлении выполнялось условие
. (4.31)
Тогда, подставляя (4.30) в (4.29), из (4.31) найдем
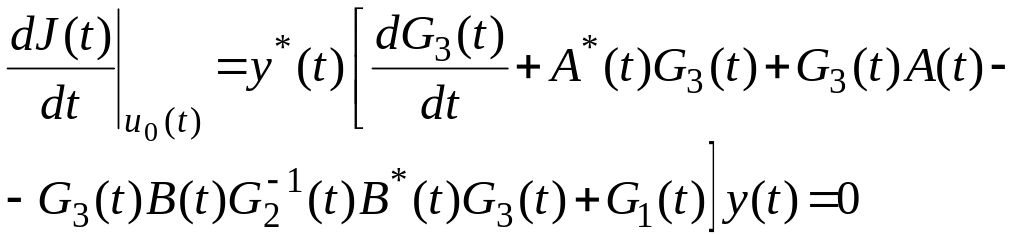(4.32)
Из условия (4.32) следует, что оно будет выполнено, если матрица будет определена из условия
(4.33)
Пусть теперь рассматривается управляемое
движение на отрезке
,
где
-некоторый
фиксированный момент времени. Потребуем
также, чтобы в момент времени
матричная функция
удовлетворяла конечному условию
(4.34)
Тогда из сравнения формул (4.24), (4.26), (4.22) и (4.30), (4.33), (4.34) следует, что локально-оптимальное управление(4.30) по критерию (4.27) с матрицей , определяемой из уравнения (4.33) с условием (4.34) совпадает с уравнением (4.24), оптимальным по квадратичному критерию (4.19) на интервале .