
- •1. Структура теоретической механики. Основы статики.
- •2. Условие равновесия произвольной системы сил.
- •3. Уравнения равновесия твердого тела.
- •4. Плоская система сил.
- •5. Частные случаи равновесия твердого тела.
- •6. Задача о равновесии бруса.
- •7. Определение внутренних усилий в стержневых конструкциях.
- •8. Основы кинематики точки.
- •Кинематика точки. Декартовы координаты.
- •9. Естественные координаты.
- •10. Формула Эйлера.
- •11. Распределение ускорений точек твердого тела.
- •12. Поступательное и вращательное движения.
- •13. Плоскопараллельное движение.
- •14. Сложное движение точки.
- •15. Основы динамики точки.
- •Законы Ньютона. Правило сложения сил.
- •16. Дифференциальные уравнения динамики точки.
- •17. Частные виды силовых полей.
- •18. Основы динамики системы точек.
- •19. Общие теоремы динамики системы точек.
- •20. Динамика вращательного движения точки.
17. Частные виды силовых полей.
1) Сила зависит только от времени – поле однородно, но не стационарно.
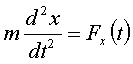 .
.
Тогда:
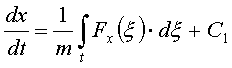 ;
;
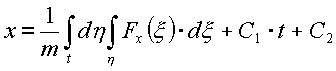 .
.
Аналогично, для y и z.
2) Проекции силы зависят только от соответствующих координат.
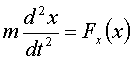 .
.
Умножая на dx и интегрируя:
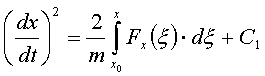 .
.
Дифференцируем снова для проверки:
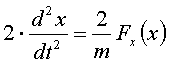 ;
;
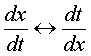 .
.
Положим:
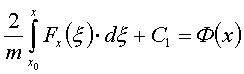 .
.
Тогда:
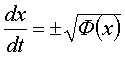
(знак берётся из начальных условий).
Разделяя переменные:
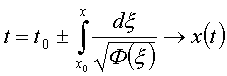 .
.
3) Проекция силы зависит лишь от проекции скорости на эту же ось.
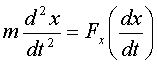 .
.
Обозначая:
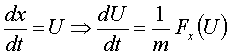 .
.
Разделяя переменные:
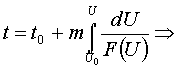
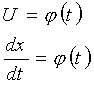
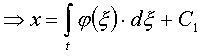 .
.
Таким образом, в каждом из трёх частных случаев силовых полей по заданным силе, массе и начальным условиям определены выражения для скорости и ускорения точки.
Контрольные вопросы:
1. В чём суть метода разделения переменных при решении дифференциальных уравнений?
2. В чём особенность интегрирования уравнения движения точки, если сила зависит только от координаты?
3. В каких реальных задачах сила зависит от скорости движения точки?
18. Основы динамики системы точек.
Рассмотрим движение n свободных материальных точек относительно инерциальной системы отсчёта (рис. 53).
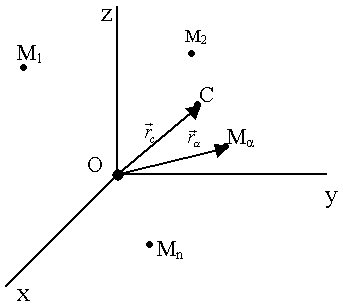
Рис.53.
![]()
![]() -
масса
точки
-
масса
точки
![]() .
.
Масса всей системы:
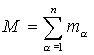 .
.
Центром масс системы назовём точку С, радиус – вектор которой равен
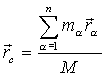 ,
,
где
![]() .
.
Основные меры движения системы материальных точек:
1. Суммарное количество движения системы (геометрическая сумма количества движения материальных точек).
![]() ,
где
,
где
![]() -
скорость
точки
-
скорость
точки
![]() .
.
Рассмотрим
систему
точек
с
постоянными
массами
=> дифференцируя
![]() :
:
 ;
;
где
![]() -
скорость
центра
масс.
-
скорость
центра
масс.
Итак,
![]()
Количество движения системы материальных точек равно количеству движения массы всей системы, сосредоточенной в центре масс.
2. Сумма моментов количества движения или кинетический момент системы:
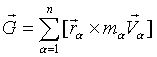 .
.
![]() представляется
в
виде
одночлена
только
в
случае
одинаковых
скоростей
всех
точек
системы.
представляется
в
виде
одночлена
только
в
случае
одинаковых
скоростей
всех
точек
системы.
3. Кинетическая энергия системы:
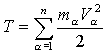
Тоже не всегда представлена в одночленной форме.
Силы разделим на внешние и внутренние.
Внешние силы действуют со стороны масс, не входящих в систему.
Внутренние силы – силы взаимодействия между точками системы.
Обозначим:
![]() -
суммарная
внешняя
сила
к
точке
-
суммарная
внешняя
сила
к
точке
![]()
![]() -
суммарная
сила
взаимодействия
точки
c
остальными
точками
системы.
-
суммарная
сила
взаимодействия
точки
c
остальными
точками
системы.
Деление на внутренние и внешние силы условно.
Получим некоторые свойства внутренних сил.
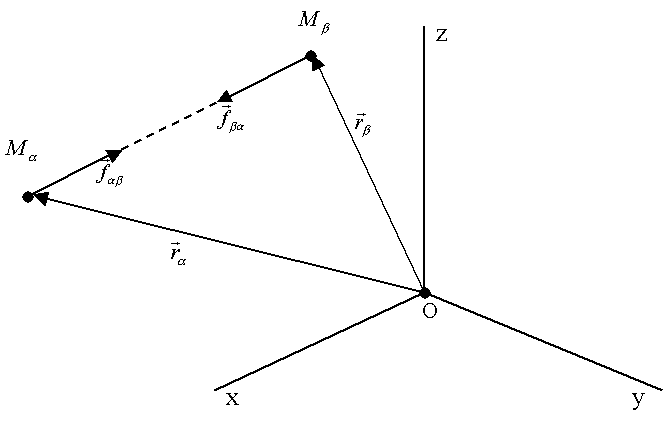
Рис.54.
Рассмотрим
точки
и
![]() (рис.
54).
(рис.
54).
Из 3 – го закона Ньютона:
![]() .
.
Внутренняя сила на точку :
![]() .
.
Очевидно:
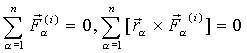 .
.
Итак, сумма внутренних сил и сумма моментов внутренних сил равны нулю относительно любой точки и любой оси.
Рассмотрим сумму элементарных работ внутренних сил.
Пусть
![]() ,
где
,
где
![]() ,
,
![]() -
расстояние
между
точками
-
расстояние
между
точками
![]() .
.
Работа
на
элементарных
действительных
перемещениях
сил
взаимодействия
двух
точек
![]() :
:
![]() .
.
[
![]() -
проекция
на
-
проекция
на
![]() ,
включающая
в
себя
знак].
,
включающая
в
себя
знак].
Обозначим
сумму
элементарных
работ
внутренних
сил
![]() :
:
(d – означает «на элементарных перемещениях»)
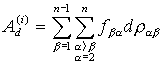
Контрольные вопросы:
1. Что называется центром масс системы материальных точек?
2. Назовите основные меры движения системы материальных точек.
3. Перечислите свойства внутренних сил системы точек?
