- •§1. Цилиндрические и канонические поверхности.
- •§2. Поверхности вращения
- •§3. Общее уравнение пов. II-го порядка. Привидение общего ур. Пов. II-го порядка к простейшим уравнениям пов. II-го порядка.
- •§8. Конус 2-го порядка.
- •§9. Эллиптический параболоид.
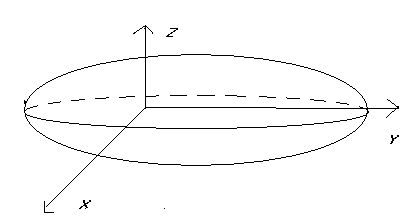
- •§5.Эллипсоид
- •§6.Однополосный гиперболоид
- •§7.Двуполостной гиперболоид
- •§10. Гиперболический параболоид.
- •§11.Цылиндры второго порядка
- •§12 .Перетин поверхні другого пор. З прямою. Асимптотичні напрямкию.
- •§15. Визначення кононічного рівняння поверхні по ортогональним інваріантам
- •§4.Поверхности, которые определяются общим уравнением поверхности второго порядка.
- •§14. Центр поверхности 2го порядка. Классификация поверхности по характеру места их центра.
- •§13 Касательна плоскость и нормаль к пов. Второго пор
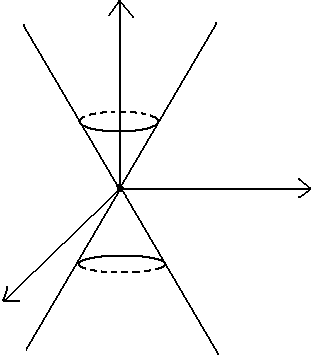
§8. Конус 2-го порядка.
Конусом 2-го порядка
называется поверхность, уравнение
которой в некоторой специально выбранной
ПДСК имеет вид :![]() (1)
(1)
Поскольку в (1) x,y,z
входят с чётными степенями, то если
точка M(x,y,z)
![]() (1),
то и точки (±x,±y,±z)
тоже
(1)
→ точка О(0;0;0) является центром симметрии
поверхности (1) и называется центром
эллипсоида. Оси координат – это оси
симметрии и называются главными осями.
Координатные плоскости являются
плоскостями симметрии и называются
главными плоскостями. Oz
– ось конуса. Если M0(x0;y0;z0)
конусу
и не совпадает с вершиной – то тогда
конусу принадлежат и все точки вида
(λx0;λy0;λz0).
Следовательно и вся пряма OM0.
Поверхность (1) образована прямыми
проходящими через точку O
и достаточно рассмотреть только сечение
плоскостями параллельными XOY:
(1),
то и точки (±x,±y,±z)
тоже
(1)
→ точка О(0;0;0) является центром симметрии
поверхности (1) и называется центром
эллипсоида. Оси координат – это оси
симметрии и называются главными осями.
Координатные плоскости являются
плоскостями симметрии и называются
главными плоскостями. Oz
– ось конуса. Если M0(x0;y0;z0)
конусу
и не совпадает с вершиной – то тогда
конусу принадлежат и все точки вида
(λx0;λy0;λz0).
Следовательно и вся пряма OM0.
Поверхность (1) образована прямыми
проходящими через точку O
и достаточно рассмотреть только сечение
плоскостями параллельными XOY:
![]()
В сечении будут
эллипсы с полуосями:![]()
Чем меньше h – тем меньше конус.
§9. Эллиптический параболоид.
Эллиптическим
параболоидом
2-го порядка называется поверхность,
уравнение которой в некоторой специально
выбранной ПДСК имеет вид :![]()
![]() (1)
q,p>0.
(1)
q,p>0.
Oz – ось симметрии эллиптического параболоида и называется осью эллиптического параболоида. Поскольку в (1) x,y входят с чётными степенями, то XOY и YOZ являются плоскостями симметрии и называются главными плоскостями. Точка O – точка пересечения параболоида с его осью и называется вершиной. Рассмотрим сечение с плоскостью:
|| XOY
![]() В
результате получим: при h<0
– Ø; h=0
– вершину параболы; h>0
– эллипс с полуосями.
В
результате получим: при h<0
– Ø; h=0
– вершину параболы; h>0
– эллипс с полуосями.![]() .
Чем больше - h
тем больше размер эллипса.
.
Чем больше - h
тем больше размер эллипса.
|| XOZ
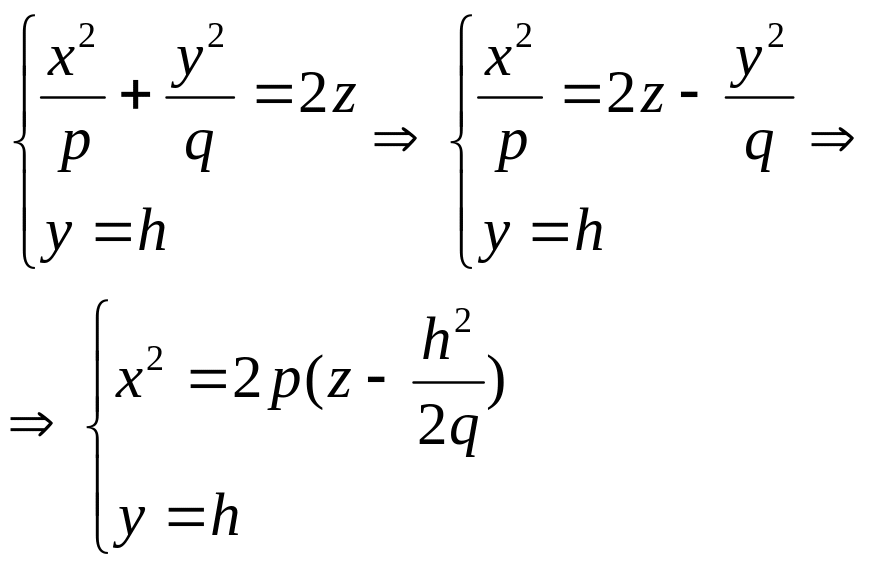
В итоге получаем параболу с вершиной в точке (0;h;h2/2q).
Аналогично будет с плоскостями в сечении YOZ.
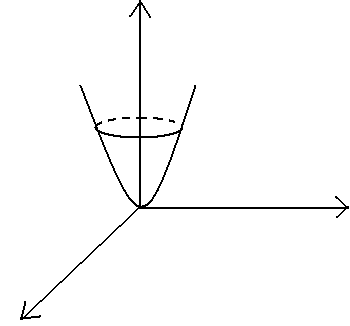
§5.Эллипсоид
Эллипсоидом
называется уравнение поверхности
которой в специально выбранной ПДСК
имеет вид:
![]() (1)
(1)
Определим по Ур. (1) вид поверхности. Поскольку в (1) x,y,z входят с четными степенями, то если точка М( x, y, z) лежит на поверхности (1), то и точки (± x, ± y, ± z) также принадлежат поверхности (1). Следовательно точка О является центром симметрии (1) и называется центром эллипсоида. Оси координат являются осями симметрии и называются главными осями. Координатные плоскости являются плоскостями симметрии и называются главными плоскостями. Вершинами эллипсоида являются точки пересечения эллипсоида его главными осями.
(± a, 0, 0) (0, ± b, 0) (0, 0, ± c)
Из уравнения (1) следует, что │x│ ≤ a │y│≤ b │z│≤ c
Следовательно эллипсоид лежит внутри прямоугольного параллелепипеда с вершинами (± a, ± d, ± c).
Рассмотрим сечение эллипсоида плоскостями параллельными координатным плоскостям.
Плоскость параллельна XOY
![]()
│h│>c пересечений нет.
│h│=с
в пересечении будет одна точка.
Следовательно плоскости z
= ± c
являются касательными к эллипсоиду.
│h│<
c
то в сечении будет эллипс с полуосями
![]()
Аналогично при сечении эллипсоида плоскостями параллельными XOZ и YOZ получим эллипсы. Следовательно в ПДСК эллипсоид имеет следующий вид: